柴油机振动信号快速稀疏分解与二维特征编码*
王 旭, 岳应娟, 蔡艳平
(火箭军工程大学理学院 西安,710025)
引 言
柴油机运行中既有旋转运动,又有往复运动,其振动响应信号复杂,耦合严重,具有较强的非线性、非平稳时变特征[1]。采用时频分析是通过对柴油机振动时频图像的识别来实现对故障的诊断,其技术关键在于准确的时频表征和有效的特征提取,众多学者对此进行了大量的探索。文献[2]提出利用灰度共生矩阵提取柴油机振动信号三阶累积量图像的故障诊断方法。文献[3]将Wigner分布与分形维数相结合,对柴油机进行故障诊断。文献[4]将图像分割理论引入柴油机故障诊断之中。文献[5]提出基于经验模态分解和维格纳分布的柴油机振动信号时频表征方法。以上方法将柴油机的故障诊断问题转化为柴油机振动时频图像的模式识别问题,取得了较好的效果。
时频表征方面,利用小波分析(wavelet analysis,简称WT)、维格纳分布(Wigner-Ville distribution ,简称WVD)及短时傅里叶变换(short time Fourier transformation,简称STFT)等方法对柴油机缸盖振动信号进行时频表征是应用较广泛的信号处理手段[6]。匹配追踪算法(matching pursuit,简称MP)是一种基于过完备冗余时频字典对信号进行稀疏分解的方法,相比于以上时频分析方法,MP算法自适应性更好,对时频分布中各分量的刻画能力更强。但是MP算法计算量和存储量相当大,限制了其在柴油机振动信号处理中的应用[7]。
特征提取方面,为了不依靠先验知识实现对不同工况时频图像的自动分类,需要对时频图像进行特征提取,其本质是对时频图像数据降维的同时最大限度保留不同样本间的差异化信息。非负矩阵分解算法(non-negative matrix factorization, 简称NMF)是一种基于局部特征的矩阵分解方法,由于添加了非负的限制条件,能够保证分解结果的可解释性。文献[8-9]将NMF应用于柴油机和轴承时频图像矩阵的特征提取,取得了较好的效果。但是NMF算法在降维前需将图像矩阵向量化处理,破坏了图像矩阵间的空间位置信息,并且向量化处理后的图像矩阵往往维数较高,使得NMF的计算效率较低。对此,文献[10-12]从不同角度提出了二维非负矩阵分解(2-dimensional non-negative matrix factorization, 简称2DNMF)方法,分解前不需将图像矩阵向量化,提高了特征提取效果,被成功应用于故障诊断领域[13-14]。但是2DNMF在分解前都是将所有训练图像矩阵按行或列拼合,拼合后的初始分解矩阵维度依然较大,并且2DNMF算法没有考虑到不同类图像间的差异化信息,将所有图像样本一致对待,统一求解投影矩阵,这显然是不利于模式识别的。
基于以上分析,笔者着眼于柴油机故障诊断中的时频表征与特征提取过程,针对MP算法分解效率问题和2DNMF特征提取性能问题,提出了基于AMP算法和双向二维非负矩阵分解的柴油机振动信号时频分析方法。将该方法应用于气门间隙正常、气门间隙过小、气门间隙过大和气门漏气4种不同气门状态信号的诊断试验中,故障识别正确率最高可达100%,充分证明该方法用于柴油机自动故障诊断的有效性。
1 信号的稀疏分解及时频表征
1.1 改进的自适应MP算法实现
匹配追踪算法在计算和存储上的瓶颈主要在于过完备字典的制备,在分解时需要遍历一个庞大的原子字典中的所有原子后再找到最匹配的原子组合。柴油机振动信号通常会聚集于有限宽度的频带中,而Gabor原子具有最好的时频聚集性,所以利用Gabor原子字典分解信号时对其他频率范围内原子的搜索过程其实是无意义的。如果令字典随残余信号的功率谱分布自适应更新,缩小原子搜索范围,在保证算法稀疏性的基础上可以大幅提高算法的计算效率。基于此,笔者提出了自适应匹配追踪算法。
设H为Hilbert空间,D={gγ(t)}γ∈Γ为H中过完备字典。原子gγ(t)由参数γ描述。Gabor原子[15]可表示为
(1)
其中:g(t)=e-πt2为高斯窗函数;原子参数γ=(s,u,ξ);s为尺度因子;u为位移因子;ξ为频率因子。
原子经归一化处理后‖gγ(t)‖=1。设f为待分解信号,且f∈H,有
(2)
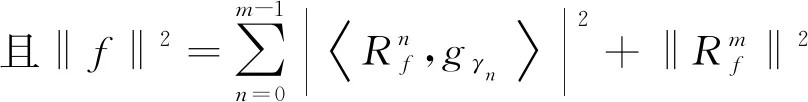
(3)
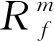
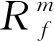
(4)
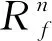
(5)
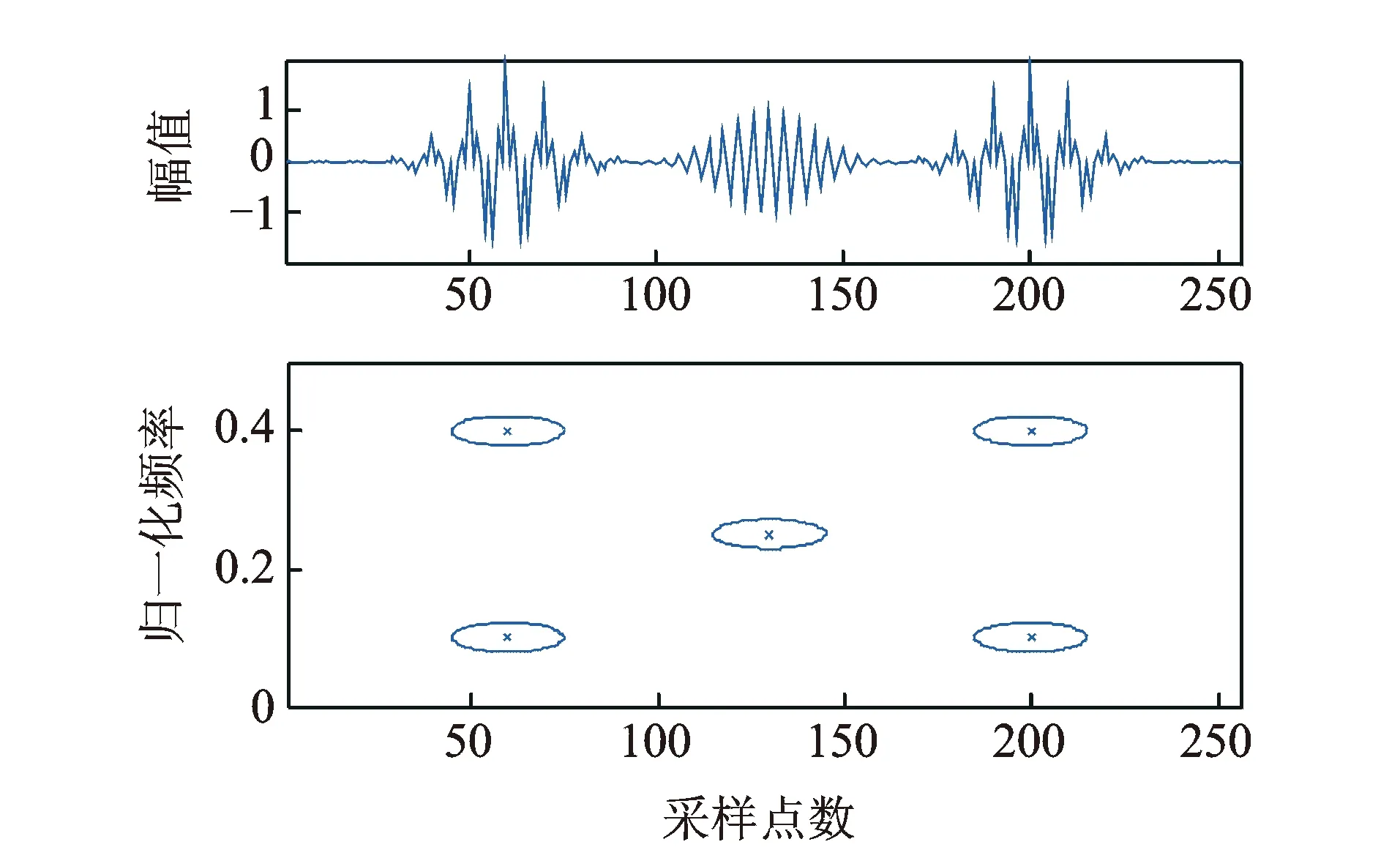
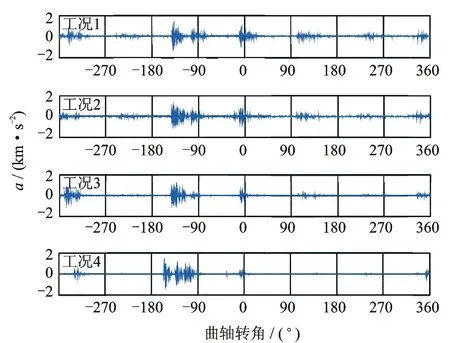
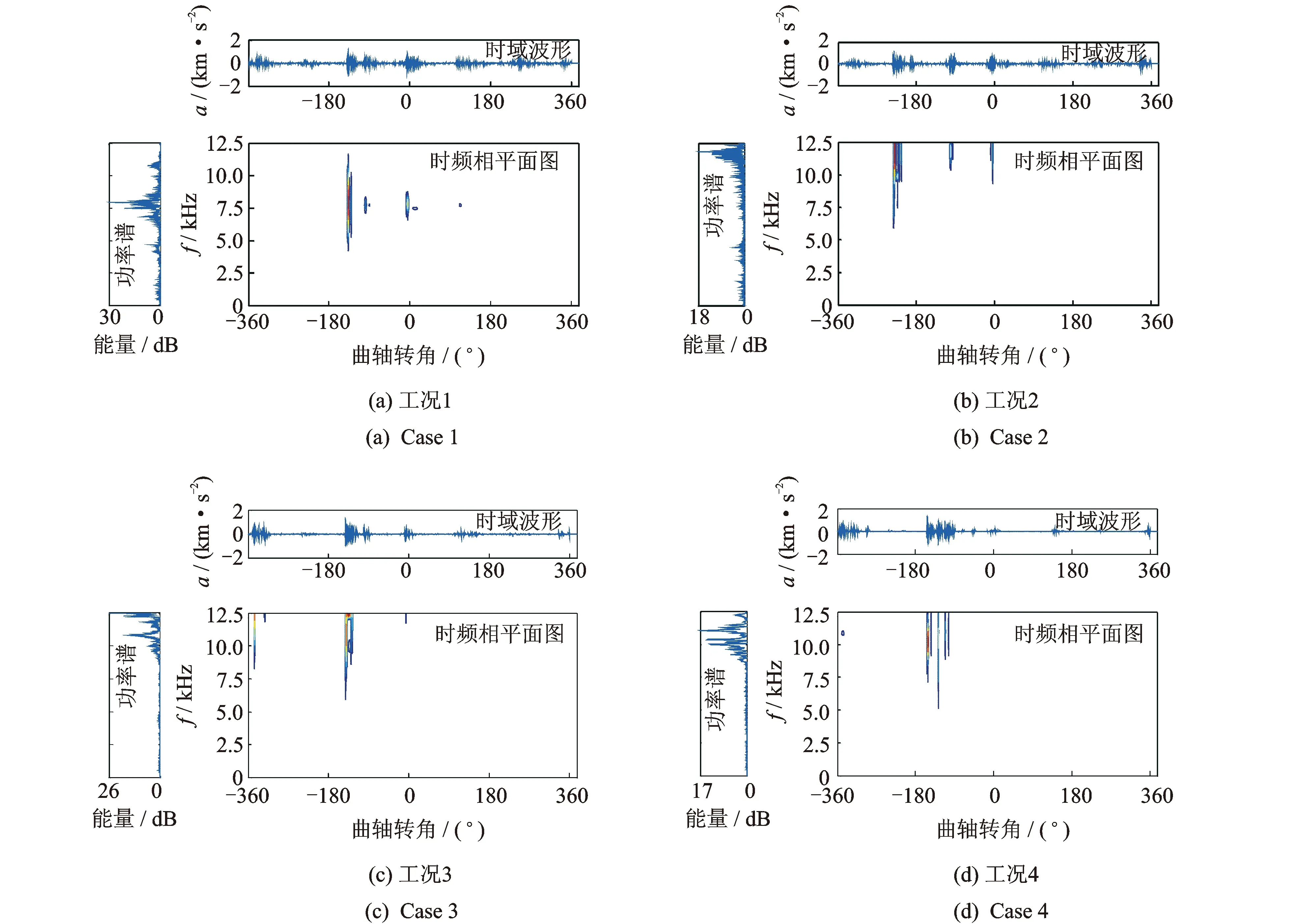
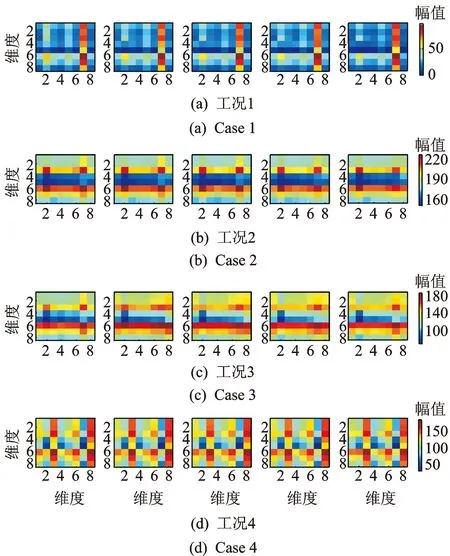
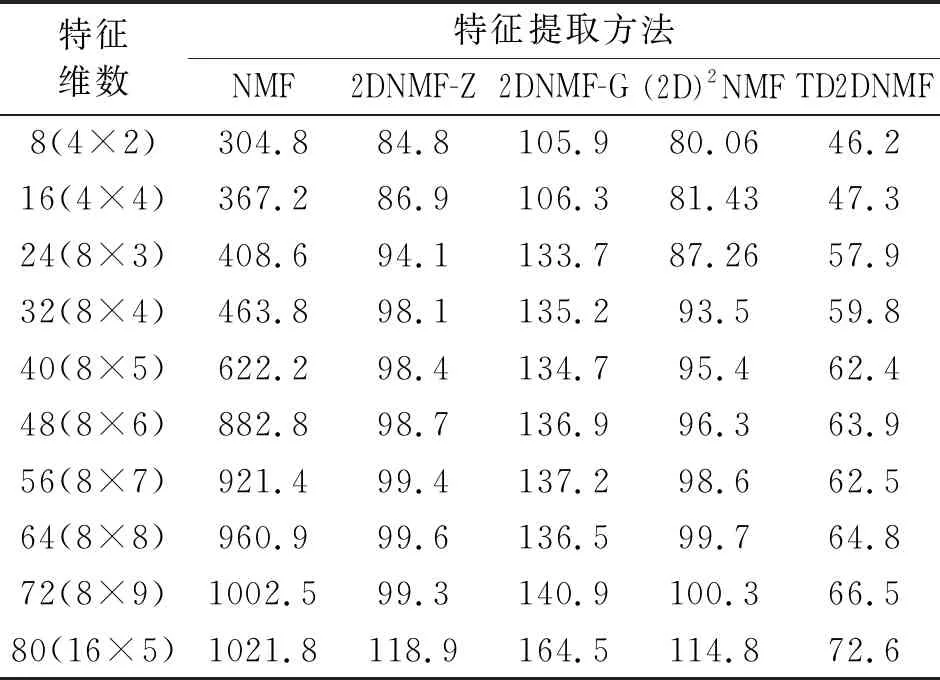
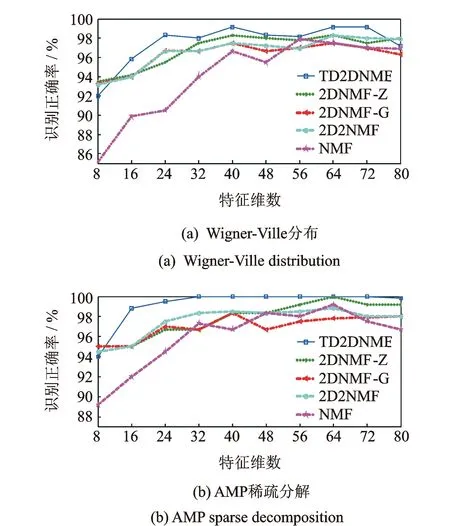
Gabor原子在频域的能量主要集中在以调制频率为中心的频率区域内,自适应字典Dn中所有的原子主要能量均聚集于中心频率ξ0附近,使得该字典中的原子和残留信号能有较好的匹配性。新字典为Dn的参数集合Γn∈R+×R中包含γ=aj,pajΔu,kajΔξ,a=2,Δu=1/2,Δξ=π,0 AMP算法流程如下。 1) 定义s=2j,其中:j∈(0,log2N);u=s。计算原子gγ的包络g((t-u)/s),并保存为包络库。由于Gabor原子的能量主要集中在区域0,2s内,为了减少计算量,每个包络可以只计算区域0,2s内的数值点。 4) 找到上步运算中的互相关系数最大值,确定相应的匹配到的原子参数。 为分析AMP算法的性能,建立一个多分量仿真信号x(t),信号长度为256,由5个具有高斯包络的原子信号分量叠加而成,采样频率归一化为1 Hz,5个信号分量的时、频域分布中心分别位于(t1,f1)=(60,0.1),(t2,f2)=(60,0.4),(t3,f3)=(130,0.25),(t4,f4)=(200,0.1)和(t5,f5)=(200,0.4),仿真信号表达式为式(6)。信号的时域波形与时频域分布对应如图1所示。 (6) 图1 仿真信号时域波形及时频域分布对应图Fig.1 The time and frequency domain waveform 表16次迭代残余信号能量及耗时 Tab.1Residualsignalenergyandtimecostin6iterations 迭代次数MP耗时/msAMP耗时/msMP残余能量/%AMP残余能量/%1504.0434.64982.6479.072394.4732.43664.6258.173382.0442.13244.0437.274397.4592.00223.3119.175418.7642.5012.951.076481.9362.1092.150.82 表1为6次迭代过程中MP与AMP两种算法对应的原子匹配时间和残余信号能量百分比。理论上,仿真信号由5个原子分量复合而成,所以无论MP算法还是AMP算法都应在5次迭代后匹配出所有原子分量。MP与AMP算法在第5次迭代后,残余信号的能量分别达到了2.15%和0.82%,均较好地匹配出了信号的原子分量,实现了信号的稀疏分解。由于本研究中AMP算法根据残余信号功率谱分布将搜索字典限定在固定频带中,其搜索到的原子对于分解信号的匹配性更好,所以每次迭代中AMP算法的残余能量都低于MP算法。同时,由于AMP算法中自适应匹配的原子字典较MP算法中的过完备冗余字典维度有较大幅的压缩,使得AMP算法较MP算法的计算效率提高了150~200倍,从而能够利用AMP算法对高维度、强耦合的信号进行分析。 为了获得信号的时频分布,利用AMP算法将仿真信号分解为5个原子分量,通过二次叠加每个原子的Wigner-Ville分布得到原信号的时频分布。仿真信号的WVD分布与AMP稀疏分解时频分布情况如图2所示。 图2 仿真信号时频分布Fig.2 Time-frequency distribution of the simulation signal 由图2看出,直接对仿真信号进行WVD分析,每两个原子之间都会产生一个交干扰叉项,严重影响对原信号分量的分析。利用AMP算法得到的信号稀疏分解时频分布中交叉项的问题得到了很好的解决,所有原子分量能量分布均衡,且保持了优良的时频聚集性,所以利用AMP算法对柴油机振动信号进行稀疏分解,能够使各时频分量物理意义更加明确,有利于对柴油机故障的判别。 为了获得更好的特征提取效果,笔者提出一种双向二维非负矩阵分解算法,其与NMF,2DNMF有着相同的目标函数及迭代规则,但是架构不同。TD2DNMF算法分别对行基、列基矩阵进行求解,进一步得到TD2DNMF的二维基,用于对时频图像进行特征编码。 首先,对行基进行求解,求解时考虑到不同类别样本的差异性,对各类别样本矩阵并行运算得到相应的基矩阵和系数矩阵;然后,组合成整个训练样本的行基投影矩阵和系数矩阵,由此得出的系数矩阵具有更好的稀疏度。假设有k类模式ω1,ω2,…,ωk,每类模式有m个训练样本图像Aa,b,a=1,2,…,k;b=1,2,…,m,每个图像对应大小为p×q的矩阵。将所有图像用矩阵X表示为 Xp×qmk=[X1,X2,…,Xk] (7) 其中:Xa=[Aa,1,Aa,2,…,Aa,m];a=1,2,…,k。 对于非负矩阵Xa,求解非负矩阵La和Ha,满足 (8) 其中:Xa∈Rp×qm,La∈Rp×r,Ha∈Rr×qm;r为特征维数,满足(p+qm)r 为了描述X≈L·H的近似效果,利用矩阵X与L·H间的K-L 散度作为近似误差,对应的目标函数[16]为 (9) 其对应的优化问题为 minD(V‖WH)s.t.W,H≥0 (10) 相应的迭代规则为 Hrj←Hrj∑iLirXij/(LH)ij (11) Lir←Lir∑jHrjXij/(LH)ij (12) (13) 由此得到每一类别图像数据矩阵对应的分解矩阵因子,对于矩阵Xp×qmk对应的TD2DNMF分解因子可由每一类别的分解因子组合而成 (17) (18) 与行基的求解过程类似,根据K-L散度构造目标函数进行迭代运算,确定列基分解的特征维数d,得到矩阵HT对应的TD2DNMF分解因子 (19) 任意图像矩阵Ap×q在行基和列基上的投影系数矩阵为 (20) TD2DNMF的二维基定义为 B=LRT (21) 通过将柴油机振动时频图像向TD2DNMF的二维基进行投影,可得到相对应的特征编码。利用分类器对特征编码进行识别,可实现时频图像的自动分类,进一步可实现对故障的判别。 基于AMP振动信号稀疏分解与TD2DNMF二维时频特征编码的柴油机故障诊断方法流程如图3所示。 图3 故障诊断流程框图Fig.3 The flowchart of fault diagnosis 以6135G型柴油机为研究对象,用加速度传感器测量缸盖振动信号,试验平台如图4所示。分别将气门间隙设置成不同状态,用以模拟气门的不同间隙异常故障。在转速稳定于1 500 r/min时测量第2缸的缸盖振动信号,单通道采样频率为25 kHz,试验具体工况设置如表2所示。试验中运行状态为空载,气门正常间隙值为0.30 mm,使用0.06 mm模拟气阀间隙过小,使用0.50 mm模拟气阀间隙过大,在气阀上开4 mm×1 mm孔来模拟严重漏气故障。共采集柴油机气门4种状态下各60组振动信号,总计240个样本。 表2 4种试验工况设置 图4 试验平台及传感装置设置Fig.4 Experimental Platform and sensing device 图5为4种工况下振动信号的时域波形。进气门开启的角度在310°附近,关闭的角度在-120°附近;排气门开启的角度在120°附近,关闭的角度在-310°附近,柴油机在0°产生燃烧激振。 图5 信号时域波形Fig.5 Time domain waveform of signal 图6 4类工况信号分解重构信号及残余信号Fig.6 Signal construction and residues of four states 用AMP算法对振动响应信号进行分解和重构,迭代200次后残余信号能量达到原信号能量的5%以内。4种工况分解的重构信号和残余信号如图6所示。可以看到,原信号中的所有冲击分量均得到了很好的匹配。在时频域上对振动信号进行分析,将AMP分解原子的Wigner-Ville分布进行叠加得到各工况的时频分布图像,如图7所示。 对柴油机振动信号进行AMP时频表征,4类工况信号分别耗时9.022,8.678,8.869和8.955s,平均耗时8.881s,而相同条件下对振动信号直接进行WVD时频表征,4类工况信号平均耗时814.65s,说明AMP时频分析方法更能够满足柴油机故障诊断的时效性。从图7可以看出,正常工况对应的频率能量较大,曲轴转角0°处对应能量更高,说明混合气体燃烧效率更高。状态2,3,4对应的频率能量小,说明气体燃烧做功不充分。对于状态2,4,由于气门漏气会导致燃烧不充分,状态4的漏气最严重,所以状态4的燃烧功率最低。气门间隙故障不但影响混合气体的燃烧效率,而且影响气门落座对缸盖的冲击。对比状态2,3和4曲轴转角-310°处频率能量,状态3的频率能量明显大于状态2,可以知道状态3的排气门间隙大,而状态2的排气门间隙小。 图7 4类工况的AMP时频分布情况Fig.7 AMP time-frequency distribution of four states 通过以上分析,时频图像清楚地表明不同间隙的气门落座冲击以及混合气体的燃烧效率所占的频率分量是不同的。因此,柴油机振动信号的稀疏分解时频图像能够较好地反映出故障特征。但是,以上分析需要一定的先验知识做前提,要依靠计算机实现故障的自动诊断,需进一步提取时频图像中的特征参量。 取采集到的240个信号作为研究对象并分别绘制时频图像,由于彩色图像对应的是三维矩阵,为了便于计算机处理,对图像进行预处理,采用阈值平均法将其转化为灰度图像,相应得到240个420×560像素点的矩阵样本。 图8为特征维数R=d=8时,柴油机4类工况振动信号时频分布图像测试集对应的特征编码。图中每个像素的幅值严格与样本系数值对应,由于文章篇幅有限,每种工况下选取5个样本显示,每个样本编码图的横、纵坐标仅代表矩阵维度。图中每一行代表一种柴油机工况,从上到下依次为气门间隙正常、过小、过大和严重漏气工况。可以看出,TD2DNMF对数据进行了有效降维,将420×560维数据压缩到8×8维,大大降低了模式识别的计算复杂度。同种工况的编码矩阵类内差异小,不同工况间编码矩阵的类间差异较大。对图像进行TD2DNMF特征提取,在对数据进行有效降维的同时,不同工况对应时频图像间的差异化信息得到了较大程度的保留,有利于提高故障模式识别的正确率。 图8 4类工况时频图像特征编码Fig.8 Feature code of time-frequency distribution of 4 states 为比较不同算法的计算效率,分别利用传统非负矩阵分解算法、文献[10]提出的二维非负矩阵分解算法(2-dimensional NMF-Zhang,简称2DNMF-Z)、文献[11]提出的二维非负矩阵分解算法(2-dimensional NMF-Gu,简称2DNMF-G)、文献[12] 提出的并行二维非负矩阵分解算法((2D)2NMF)以及笔者提出的TD2DNMF算法对4种工况所有样本进行特征提取。NMF特征维数设定为二维方法编码矩阵行、列维数的乘积。4种算法统一最大迭代步长为100,目标函数容忍误差为10-5。表3为5种算法特征提取的计算时间,均不包含图像载入的时间。试验环境为 Matlab R2012b,AMD A8处理器,1.90 GHz主频CPU,4GB内存,Win7操作系统。 由表3可见,随着特征维数的增加,5种算法特征提取时间整体呈增长的趋势。二维NMF的计算效率明显要高于一维NMF,一维NMF对图像矩阵进行向量化后数据矩阵维度过大。例如,笔者所用图像维度为420×560,120幅训练图像组成的数据矩阵维度为120×235 200,计算任务量十分繁重。二维NMF算法中,2DNMF-G的计算效率略低于其他几种,这是由于2DNMF-G在计算时将原始图片分别按行、列拼合,初始分解矩阵维数分别为420×67 200和560×50 400,数据维度依然很大。(2D)2NMF算法在初始分解矩阵的组成上与2DNMF-G相同,但是采用并行运算的方法,计算效率有所提高。2DNMF-Z算法的初始分解矩阵仅将图像按行拼接,再将一次NMF分解后得到的系数矩阵分块转置再拼接后作为新的初始分解矩阵进行求解,两个初始分解矩阵的维度分别为420×67 200和560×960,维度小于2DNMF-G与(2D)2NMF,计算效率与后者相当。本研究方法TD2DNMF将图像矩阵按行拼接后按照各自的类别进行分解,将得到的4个系数矩阵各自分块转置再拼接,组成新的初始分解矩阵,两次分解的数据矩阵维度分别为420×67 200和560×120。与其他几类算法相比,本研究方法初始分解矩阵维度更低,有效提高了算法的计算效率。 为比较5种方法特征提取效果,采用最近邻分类器(nearest neighbor classifier, 简称NNC)对提取到的特征参数进行模式识别。诊断时分别采用柴油机振动信号的Wigner-Ville时频分布图和AMP稀疏分解时频分布图的240个样本,每种工况60个样本,从中随机抽取30个作为训练样本,其余作为测试样本。以NNC分类正确率评价5种方法的特征提取效果,为减小随机误差,试验重复10次取平均准确率作为最终结果,如图9所示。 表3不同方法特征提取效率对比 Tab.3Timecostindifferentfeatureextractionmethodss 特征维数特征提取方法NMF2DNMF-Z2DNMF-G(2D)2NMFTD2DNMF8(4×2)304.884.8105.980.0646.216(4×4)367.286.9106.381.4347.324(8×3)408.694.1133.787.2657.932(8×4)463.898.1135.293.559.840(8×5)622.298.4134.795.462.448(8×6)882.898.7136.996.363.956(8×7)921.499.4137.298.662.564(8×8)960.999.6136.599.764.872(8×9)1002.599.3140.9100.366.580(16×5)1021.8118.9164.5114.872.6 图9 不同特征提取方法分类性能对比Fig.9 Performance of classifier based on different feature extraction methods 图9(a)可以看出,使用3种分类方法对WVD时频分布图进行特征提取,其中NMF的识别率相对较低,2DNMF-G和(2D)2NMF的识别准确率相差不大,各个特征维度的识别准确率都在90%~98%之间,特征维数大于32时2DNMF-Z的识别率稍高,整体来看TD2DNMF特征提取效果最好。但是由于WVD分布中交叉项的干扰,会对故障类别带来较大影响,所以其识别正确率最高为99.17%,稳定于98%上下。图9(b)中,3种分类方法对AMP稀疏分解时频分布图进行特征提取,识别率与图9(a)中相比,5种方法均有所提高。这是由于采用AMP对柴油机振动信号进行时频分析时,生成的时频分布时频聚集性更好,各个工况间的差异更明显,也更利于分类器的分类。TD-2DPCA在特征矩阵维度为8×4和更高维度时,识别准确率稳定在100%,直到特征维数为80时识别率才降为99.83%。对比图9(a)和(b)可以发现,采用基于AMP稀疏分解与TD2DNMF特征编码的故障诊断方法更适用于柴油机气门间隙故障的诊断,并具有较高的诊断精度,且对于一个测试信号样本而言,整个诊断过程运行时间平均为9.483s,运行效率较高。 为了与图像方法形成对比,笔者在振动信号的频域进行故障特征的提取。利用经验模态分解方法(empirical mode decomposition,简称EMD)将信号分解为有限阶的内禀模态函数(intrinsic mode function,简称IMF)之和,剔除伪分量后保留了前三阶IMF。利用AR参数模型求解前三阶IMF的功率谱,采用最终预测误差准则判断最优阶次,使用Yule-Walker方法估计AR模型参数,将每阶IMF的前8个AR参量作为特征向量,仍使用NNC作为分类器进行模式识别,训练集、测试集样本个数与前文保持一致,平均识别正确率为86.67%。相比而言,振动信号的时频图像中既包含了信号时域中各时频分量的产生及消亡时刻的信息,又包含了频域中信号的能量分布信息,对柴油机振动信号非平稳时变特征具有较强的刻画能力。 1) AMP算法利用随分解残差信号自适应更新的Gabor字典,通过原子与残留信号的互相关运算选择最优原子,与原始MP算法相比,运算速度得到了大幅提高,同时也保持了良好的稀疏性能。 2) TD2DNMF算法将数据矩阵行、列维信息融合到一个判别分析框架中,将不同类别的数据信息并行运算,对柴油机振动时频图像样本进行特征编码。与现有几种二维NMF分解算法相比,TD2DNMF算法能更有效地提取柴油机振动时频图像的差异特征,计算效率也得到了提高。 3) 利用AMP算法分解振动信号,叠加匹配原子的Wigner-Ville分布所得到的时频分布具有很高的时、频分辨率且无交叉项的干扰。用该方法对柴油机不同气门间隙工况的振动信号进行分析,各工况的时频分布特征明显,时频分量物理意义明确。AMP稀疏分解与TD2DNMF特征编码相结合的故障诊断方法用于柴油机故障诊断中可获得较高的诊断精度,是一种有效的机械设备故障诊断方法。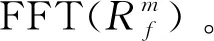
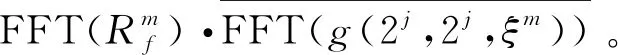
1.2 仿真分析


2 基于双向2DNMF的时频特征编码方法


3 柴油机故障诊断实例分析
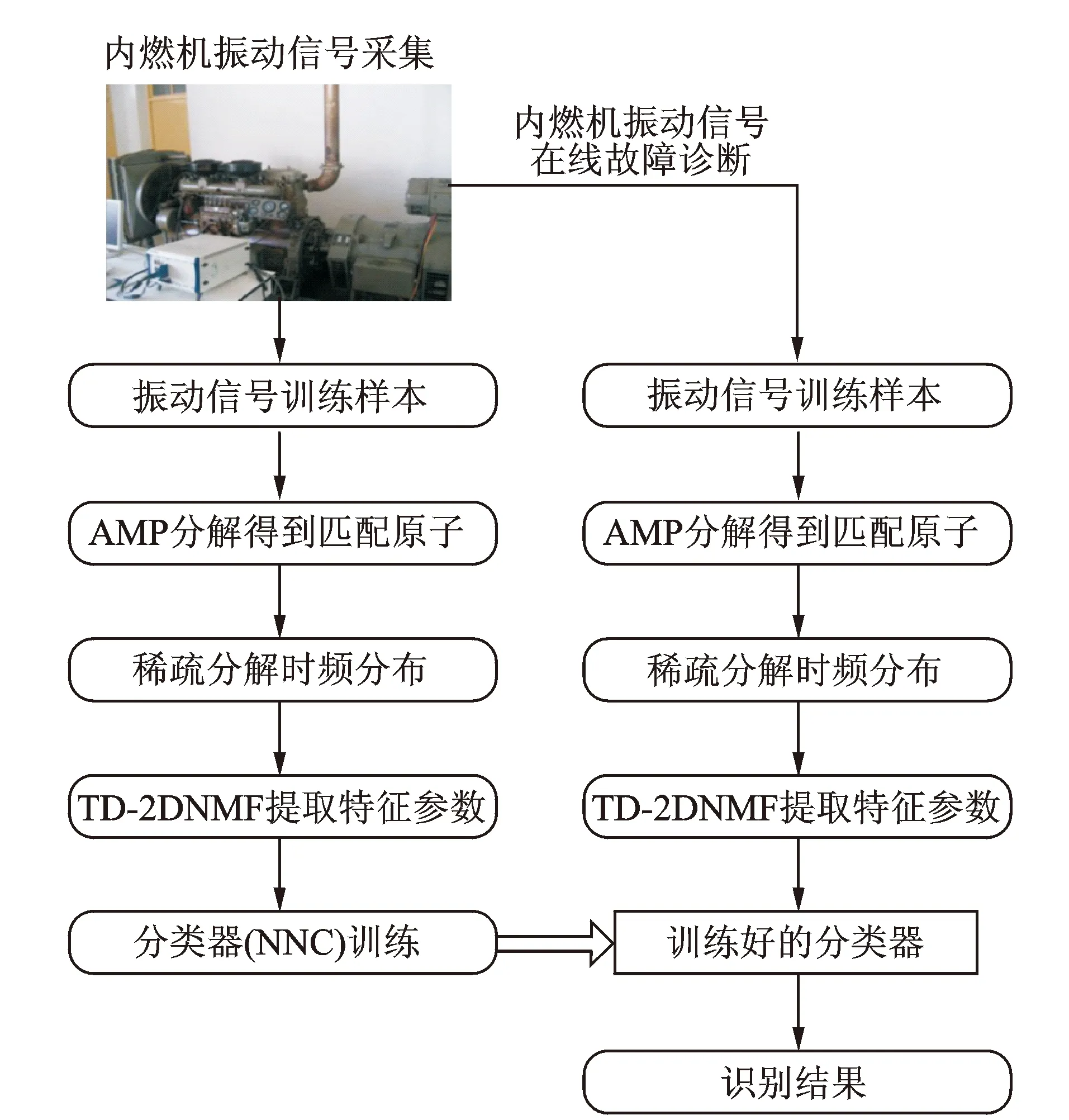
3.1 试验设备与工况设置

3.2 信号稀疏分解生成时频图像

3.3 TD2DNMF时频特征编码提取与故障识别

4 结 论

