传感器故障后多变量经验小波变换多点预测*

2019-02-27 01:51李春祥张佳丽

振动、测试与诊断 2019年1期

李春祥，张佳丽

(上海大学土木工程系上海，200444)

引言

目前超高层建筑，特别是600 m以上超高层建筑需要安装结构健康监测(structural health monitoring，简称SHM)系统，通过对结构响应等结构系统特性分析来监测结构损伤或退化。SHM系统使用的传感器属于精密测量仪器，使用环境恶劣、操作不当和安装不稳定等因素都会导致故障发生。据资料显示，最严重的风灾往往由飓风和雷暴产生。在风灾发生时，一旦传感器发生故障，对数据记录造成缺失，后果难以挽回。另外，在结构振动的主动控制中，整个建筑物表面所受的力需要同时得知，若多个传感器同时发生故障，单点预测不能满足计算需要，因此多点同步预测模型的建立十分必要。

要同步恢复缺失信号，必须要考虑同步分解多变量信号。随着多变量信号分析的需求增加，Rehman等[1]提出MEMD算法来代替传统经验模态分解(empirical mode decomposition, 简称EMD)这种单通道信号分解方法。该算法能同步处理安放在不同位置的传感器采集来的多变量信号，保证了固有模态函数(intrinsic mode function，简称IMF)在数量和尺度上的统一。近年来，MEMD常被用于机械状态的监测和故障的诊断，极大地提高了多变量信号分解的准确性，同时降低了运算的复杂程度。Yong等[2]验证了MEMD结合非局部均值 (non-local means，简称NL-means)降噪算法以及故障相关因素分析在滚动轴承故障诊断中的有效性。Huang等[3]提出一种部分噪声辅助的多元经验模态分解(partial noise assisted multivariate EMD，简称PNA-MEMD)算法，利用高频窄带的噪声来取代传统的白噪声，获得稳定效果的同时简化了运算。熊炘等[4]利用MEMD分解多通道振动信号来融合识别齿轮箱齿面点蚀故障信号的多通道数据。王恒等[5]采用自适应噪声辅助的多元经验模态分解(noise assisted multivariate EMD，简称NA-MEMD)来提取故障特征。段若晨等[6]提出一种窄带噪声辅助多元经验模态分解(narrowband noise assisted multivariate empirical mode decomposition，简称NNA-MEMD)算法，用来检测换流变压器用有载分接开关的机械状态。从以上发展看出，NA-MEMD是一种常用多变量分析的算法，能一定程度上解决MEMD的模态混叠问题。考虑到经验小波变换(empirical wavelet transform, 简称EWT)在单点信号分解中有很好的效果，利用EWT基本框架构建MEWT算法，对故障后的多变量信号进行同步恢复，同时采用MIMO策略代替传统的滚动策略进行多步预测，提高精度的同时能获得更长时间的预测值，并与NA-MEMD模型进行对比，说明MEWT模型的优越性。

1 MEWT-KELM-CS-MIMO多点同步多步预测模型

1.1 EWT基本原理

近年来，在非线性、非平稳信号去噪方面，小波变换(wavelet transform, 简称WT)和EMD等都取得了一定效果，但WT在强噪声情况下去噪效果会退化，EMD存在数学理论缺失、对噪声和取样敏感的问题[7]。Gilles等[8-9]基于小波变换和经验模态分解存在的问题，提出了经验小波变换。EWT能够通过完全自适应小波基提取信号的固有模态，与经典小波变换一样具有完备的理论基础，可以显著降低EMD类分解方法存在的模态混叠现象。

EWT的步骤总结如下：

(1)

2) 根据Meyer小波的构造方法构造一系列经验小波。对于任意的∀n>0，经验尺度函数和经验小波函数分别为

(2)

(3)

(4)

(5)

3) 重建信号。重建的序列和经验模态为

(6)

(7)

(8)

1.2 MEWT技术框架

笔者提出多变量经验小波变换的概念，通过将经验小波变换分解后的模态进行相空间重构，模态数不等用零矩阵补齐后再重构来实现同步预测。

这里以三点信号为例来展示MEWT技术框架。首先，对每个信号通过EWT分解后的模态进行以下相空间重构，即将一维时间序列转换成矩阵的形式。第i个模态的训练集的时间序列{xi1,xi2,…,xin} 进行嵌入维度为d的相空间重构，具体的输入和输出样本对为

设3个信号分解后最大模态数为m，若EWT分解后的模态数不足m的信号用零矩阵来补齐缺失的模态。

1.3 KELM基本概念

给定N个样本{(xi,yi)|i=1,2,…,N}，其中xi=[xi1xi2… xin]T∈Rn，要寻找预测函数f:x→y，使得f(x)≈y。在隐层神经元数目为L的ELM中，这个预测函数的形式可表述为

(9)

在极限学习机(extremelearningmachine, 简称ELM)中，输入权值和隐层节点偏置都是事先设定好的，激活函数也是选定的，所以ELM的训练问题可归结为求解输出权值β的问题，建立如下的最优化问题

s.t.hT(xi)β=yi-εi(i=1,2,…,N)

(10)

其中：C为正则化参数，可以人为设定；εi为松弛变量，衡量实际值与预测值之间的误差。

求解式(10)得到

(11)

其中：H=[h(x1) …h(xN)]T为隐含层输出矩阵；Y=[y1… yN]T为输出向量；IN为一个N×N维的单位矩阵。

类似于支持向量机(supportvectormachine, 简称SVM)等办法，用核函数取代特征映射h(x)，定义核函数为k(x,y)=〈h(x),h(y)〉,这里〈·,·〉表示特征映射的内积。于是可以定义核矩阵Ω为

Ω=HHT：Ωi,j=h(xi)·h(xj)=k(xi,xj)

(12)

将核函数带入式(9)和式(11)，得到KELM的预测函数为

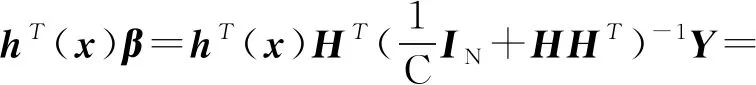
(13)

研究显示，KELM比起ELM有更好的泛化性能的同时需要更少的迭代参数[10]，KELM往往能和SVM达到相同的精度，但训练预测花费的时间更少[11]，因此笔者选用KELM作为预测模型。径向基核函数(radialbasiskernelfunction, 简称RBF)是适应性最好、使用最为普遍的一种核函数，其表达式为

K(x,xi)=exp(-‖x-xi‖2)/(2σ2)

(14)

其中：σ为RBF的宽度，也叫核参数。

1.4 CS算法概述

杜鹃搜索算法是文献[12]提出的一种新兴启发算法,采用相关的Lévy飞行搜索机制。用杜鹃鸟的蛋来代表新的解，目的是使用新的和潜在的解来代替不那么好的解。该算法基于3个理想化规则：a. 每个杜鹃下一个蛋，堆放在一个随机选择的巢中；b. 最好的高品质的蛋巢将转移到下一代；c. 巢数量固定，杜鹃的蛋被发现的概率为[0,1][13]。研究表明，杜鹃搜索比其他群体优化算法更有效。

笔者采用CS对KELM的正则化参数C和核函数参数σ进行优化，C的取值范围设定为[2-8,28]，σ2的取值范围设定为[0.01,100]，具体步骤如下：

1) 初始化参数C和σ，生成初始种群。

2) 将平均绝对误差(mean absolute error，简称MAE)作为适应度函数计算每个鸟巢的适应度，求出种群最优位置。

3) 用xi(t+1)=xi(t)+α⊕levy(λ)更新鸟巢位置，其中：xi(t)代表第i个鸟巢在t代的鸟巢位置；α为步长；⊕代表点对点乘法；levy(λ)表示莱维(Lévy)随机搜索路径，且levy(λ)～u=t-λ(1<λ<3)。将现有鸟巢位置与上一代鸟巢位置进行对比，择优作为当前最优位置。

4) 用随机数r∈[0,1]与鸟巢主人发现外来鸟概率Pa对比，若r>Pa，则随机地改变鸟巢位置，得到一组新的鸟巢位置。

5) 比较各鸟巢适应度值，更新当前鸟巢最优位置。

6) 满足容许值停止迭代，否则重新执行步骤3。

7) 得到最优参数。

有研究表明，由于CS算法搜索过程采用Lévy飞行，短距离的探索与长距离探索相间，因此CS在迭代后期有更强的优化能力[14]。同时，有研究指出，CS算法和粒子群优化(particle swarm optimization, 简称PSO)算法都能收敛到全局最优，但是仍有机会陷入局部最优[15]，因此对每种情况运行10次求平均值得到最终结果[16]。

1.5 MIMO策略用于多步预测

在时间序列预测中，往往希望了解未来一段时间的数值或者趋势，为了获得更长时间的预测值而增大序列的间隔时间往往导致信号信息丢失和预测值不能用于实时调度的问题，多步预测就成为一种重要方法。因为采用多输入单输出函数，先前的多步预测策略，例如滚动策略、直接策略和直接滚动策略被认为是单输出的策略，影响多步预测精度的主要因素有误差的积累、准确性的降低和不确定性的增加[17]。MIMO策略能避免上述单输出策略引起的未来预测值之间的联系被丢失的情况，提高准确性，降低不确定性，同时MIMO策略一次输出所有步长预测值，消除了滚动法中的误差积累现象，因此MIMO 策略相比于其他多步预测策略有更高的预测精度。近年来，多篇文献也反应MIMO策略相比于其他多步预测策略有更高的预测精度[17-19]。另外，与直接策略以及直接滚动策略需要构建多个模型相比，MIMO策略仅需一个模型，建模简便。

MIMO策略仅需通过时间序列[x1,…,xN]来训练一个多输出模型F

[xt+H,…,xt+1]=F(xt,…,xt-d+1)+w

t∈{d,…,N-H}

(15)

以矩阵的形式表现更为直观，MIMO策略训练模型时输入矩阵为

输出矩阵为

(16)

笔者按照训练集占比75%左右的标准，选取前800个点作为训练集，即N取800，预测后200个点。在超前3步和超前6步的预测中，H分别取3和6，每次预测得到后一步长所有的预测值，循环得到后200个点的预测值。

1.6 信号恢复流程

笔者创新性地提出用MEWT-KELM-CS-MIMO模型来对多点缺失数据进行同步恢复，多步预测得到未来一段时间的预测值。整个流程框架如图1所示。具体步骤如下：

1) 按MEWT的技术框架，将多点中断信号前一定长度的时间序列进行同步相空间重构后组合成新的矩阵；

2) 将重构后的矩阵分为训练集和测试集；

3) 归一化处理能提高预测的精度和收敛的速度，将新组合成的矩阵归一化到[-1,1]；

4) 径向基核函数极限学习机用来训练和预测，其中正则化参数和核参数用CS算法优化。

5) 将各模态的预测值相加得到预测结果，计算评价指标评价模型；

6) MIMO策略用来实现模型的1步预测、3步预测和6步预测，并与滚动策略对比。所提出的模型还与EWT-KELM-CS单点模型、NA-MEMD-KELM-

图1 信号恢复流程图Fig.1 Flowchart of signal recovery

CS多点同步模型通过评价指标进行对比，最终证明MEWT-KELM-CS-MIMO多点同步模型的优越性；

7) 多步预测结果可用于传感器信号恢复，也可在结构振动控制的主动控制中提前计算结构下一步荷载。

2 基于实测风压数据的模型验证

对某办公楼楼顶砌筑的矩形结构在2012年11月23日测得的实测风压数据[20]进行研究。该测试结构位于办公楼楼顶，视野开阔，当天风向为东北风，风力为3至4级，实测方案和实测平面布置图如图2所示。在结构AB墙表面，沿竖向每隔21 cm布置1#～5#风压传感器，DA墙表面，沿竖向每隔21 cm布置6#～10#风压传感器，1#和6#风压传感器距离结构顶面18 cm，同时，所有传感器距角A水平距离均为23 cm。可知，6#～10#风压传感器位于迎风面，1#～5#风压传感器位于背风面，笔者取其中2#～4#和7#～9#传感器的实测数据来分析。

现场采样频率为20 Hz，取1 000个数据点用于模型的训练和测试，为了获得较长的时间序列，采样点之间间隔取0.8 s。

图2 实测方案和平面布置图Fig.2 Field measurement scheme and plane layout

2.1 迎风面模型验证

假设迎风面3点数据同时缺失，用MEWT-KELM-CS-MIMO模型对这3点数据同步恢复。7#，8#和9#风压数据用EWT分解后产生的模态数分别为11，12和11，嵌入维度d取10，MEWT确定模态数为12，不足12个模态的用零矩阵补齐后重构为新矩阵，之后将其分为训练集和测试集两部分。训练集取790个30维向量，测试集取200个30维向量。3种常见模型和所提出的MEWT-KELM-CS-MIMO分别预测后对比，采用以下4个指标评价4种模型的预测效果。

平均绝对误差

(17)

均方根误差

(18)

2.2 背风面模型验证

假设背风面3点数据同时缺失，用MEWT-KELM-CS-MIMO模型对这3点数据同步恢复。2#，3#和4#风压数据用EWT分解后产生的模态数分别为9，8和8，嵌入维度d取10，MEWT确定模态数为9，不足9个模态的用零矩阵补齐后重构为新矩阵，之后将其分为训练集和测试集两部分。训练集取790个30维向量，测试集取200个30维向量。3种常见模型和所提出的MEWT-KELM-CS-MIMO分别预测后对比，采用上述评价指标对各模型进行评价。3#超前1 步、3步和6步的预测结果及误差分布图如图4所示。3点的各模型预测性能评价指标如表2所示。

由表2可知，在超前1步预测时，提出的模型接近EWT-KELM-CS单点模型，在超前3步预测和超前6步预测中，对于3#和4#，所提出的模型要优于其他3种模型，对于2#，模型D效果和模型A在超前3步预测时相差不多，但是优于模型B，C。在超前3步预测时，2#模型D相对于模型B，C的ρMAE达到78.4%，17.5%；3#模型D相对于模型A，B，C的ρMAE达到9.7%，76.0%，28.8%；4#模型D相对于模型A，B，C的ρMAE达到9.7%，71.3%，25.4%。在超前6步预测时，2#所提出的模型D相对于模型A，B，C的ρMAE达到30.8%，57.7%，33.2%；3#模型D相对于模型A，B，C的ρMAE达到33.7%，54.8%，35.8%；4#模型D相对于模型A，B，C的ρMAE达到20.4%，44.6%，33.3%。

2.3 双面模型验证

随机选取迎风面和背风面的数据点用MEWT-KELM-CS-MIMO对数据进行同步预测，结果和单独预测迎风面或单独预测背风面结果相差不多。同时，从以上结果看出，3点同步预测结果中中间点和两端点效果相近，反映出笔者采用的多点同步模型不受空间的限制，仅用各点以往的数据样本来训练模型，同步预测之后的信号能达到比空间点预测更高的精度。

图4 3#预测结果和误差分布图Fig.4 Forecasting results and Error distribution diagram of 3#

模型1步预测3步预测6步预测MAERMSERMAPEMAERMSERMAPEMAERMSERMAPE2#A0.0890.1150.9990.3150.3130.4480.9930.5181.0991.3850.9302.493B0.7531.0640.9571.4741.5302.1080.8173.2951.7972.3930.7577.862C0.1210.1570.9990.3670.4010.5190.9911.6261.1391.4730.9235.576D0.1270.1620.9990.3320.3310.4540.9921.3870.7611.0970.9548.2363#A0.0960.1290.9990.7110.3720.4810.9912.7941.2071.5540.9068.253B0.7130.9830.9627.4681.4061.9660.83110.7821.7702.3390.7517.834C0.1490.1890.9991.1770.4730.5970.9863.8421.2461.5800.9077.846D0.1430.1810.9990.7600.3370.4690.9911.4840.8001.1640.9451.6634#A0.0970.1340.9990.0770.4230.5370.9890.2981.1821.4980.9131.069B0.7111.0320.9590.5181.3331.8520.8601.2501.6992.3100.7711.130C0.1410.1780.9990.0920.5120.6470.9840.3261.4111.7870.8781.396D0.1370.1750.9990.0700.3820.5170.9900.2720.9411.3440.9300.899

A为EWT-KELM-CS单点模型；B为NA-MEMD-KELM-CS；C为MEWT-KELM-CS；D为MEWT-KELM-CS-MIMO

3 基于实测强非平稳风速数据的模型验证

Derecho是一种典型的风暴，通常可以存活超过8 h以上，其特点在于具有大面积超过65节(1节=1.852 km/h)的持续强风，移速较高，破坏力很强。2002年5月20日至7月15日德克萨斯理工大学大气科学系在瑞茜技术中心由北向南布置了7个便携式塔，测得了Derecho水平风速数据。塔间间隔为263 m，其中塔1和塔7最高观测点位置高为3 m，塔2，3，5，6最高观测点位置高为10 m，塔4最高观测点位置高为15 m。选取塔4上高度为3.96, 6.10以及10.06 m处的水平风速数据来验证多点同步模型，将3.96 m处的点记为1#，6.10 m处的点记为2#，10.06 m处的点记为3#。各塔布置图及观测点位置如图5所示。原始采样频率为2 Hz，笔者采用1 Hz ，各点实测数据如图6所示。以3#为例，运用增广的迪基-福勒检验法(augmented dickey-fuller test，简称ADF)检验时间序列平稳性。若存在单位根，则为非平稳时间序列；否则为平稳时间序列。风速样本检验值为-2.820，大于1%，5%显著性水平下的临界值-3.437和-2.864，存在单位根的原假设成立，所以样本为非平稳时间序列。2#超前1步、3步和6步的预测结果及误差分布图如图7所示。2#的各模型预测性能评价指标如表3所示。

图5 各塔布置图及观测点位置Fig.5 The layout of towers and the location of observation points

图6 各点实测数据图Fig.6 Original wind speed time series

由表3可得，在超前1步预测和超前3步预测中，提出的模型效果接近EWT-KELM-CS单点模型，优于其他2种模型。但在超前6步预测时，模型D相对于模型A，B，C的ρMAE达到15.1%，62.3%，28.0%。

图7 2#预测结果和误差分布图Fig.7 Forecasting results and Error distribution diagram of 2#

模型1步预测3步预测6步预测MAERMSERMAPEMAERMSERMAPEMAERMSERMAPE2#A0.0190.0260.9990.0010.1170.1530.9970.0080.5220.6640.9510.037B0.4550.5750.9690.0320.7670.9780.9060.0551.1761.4950.8020.086C0.1020.1270.9980.0070.3270.4340.9790.0230.6150.7860.9390.043D0.0970.1230.9990.0070.2280.3370.9880.0160.4430.5850.9690.031

A为EWT-KELM-CS单点模型；B为NA-MEMD-KELM-CS；C为MEWT-KELM-CS；D为MEWT-KELM-CS-MIMO

4 结论

1) MEWT-KELM-CS-MIMO的多点同步多步预测模型预测精度高，与EWT-KELM-CS单点模型接近，满足精度要求，同时发展多点同步多步预测模型能大大提升工程应用效率。

2) MEWT-KELM-CS-MIMO模型的预测精度高于MEWT-KELM-CS模型，说明多步预测时MIMO策略优于滚动策略，与国际文献结论一致。

3) 随着步数的增加，MEWT-KELM-CS-MIMO模型精度可以超过EWT-KELM-CS单点模型，可以实现更长时间预测的同时保证精度。多点同步多步预测模型能提高计算的效率，比单点模型具有更大的工程应用价值。

4) 传统使用NA-MEMD对多维信号进行分解的方法精度较低，因为加入噪声的MEMD不能完全解决模态混叠问题，采用有良好数学基础的EWT能很好地解决这个问题，但是无法保证多点分解后模态数一致。笔者创新性采用零矩阵来补齐模态数，提出MEWT概念，得到更高精度的同步预测结果，证明了MEWT结合传统的KELM适用于多点同步预测。

5) 若传感器彻底损坏，无法带入新鲜样本，只能恢复后面一个步长的数据，要想恢复很长一段时间的数据，可以将采样间隔加大或将预测值不断滚动迭代实时分解后预测下一步长。同时多点同步多步预测模型在结构振动控制的主动控制中应用前景广阔，可以提前计算结构整个面的受力，让结构提前知道下一步的反应，减小时滞，提高效率。