基于改进的不等时距灰色模型的车辆装备冷却系金属腐蚀预测

徐安桃， 李锡栋， 周 慧， 乔渊博， 魏骏逸

(陆军军事交通学院投送装备保障系， 天津 300161)

车辆装备冷却系是一个由铸铁、铸铝、黄铜、紫铜、碳钢及焊锡等多种金属材料构成的液冷式密闭循环体系。金属材料的工作环境恶劣，若长期服役于含盐类的近弱碱性电解质溶液中，或处在常温与高温的交替环境下，极易发生腐蚀，引起水箱穿孔、发动机缸套穴蚀等损伤，从而影响车辆的正常工作[1-3]。因此，加强对车辆冷却系的腐蚀问题研究，实现对冷却系典型金属腐蚀状况的预测具有重要的现实意义。

冷却系金属材料的腐蚀是一个极为复杂的物理化学过程，其受冷却液、缓蚀剂、酸碱度和工作温度等诸多因素影响，这些腐蚀、抗腐蚀因子相互作用构成了一个复杂恶劣的冷却系环境。由于这些因子之间的关系具有很大的不确定性、模糊性，可视之为随时间而变化的灰色量，因此可通过灰色系统理论进行研究。如：刘武等[4]以输气管道腐蚀速度和深度为原始数据，建立了管道腐蚀GM(1,1)预测模型，取得了较为理想的腐蚀预测结果；程浩力等[5]基于GM(1,1)模型，采用VS2010开发了一款针对海底管道腐蚀速率的预测软件，可在较少样本条件下实现管道腐蚀速率的预测。总体来看，GM(1,1)模型能克服“贫信息、少数据”等问题，使不确定的灰色量量化，现已广泛应用于各个行业。然而，该模型仍存在一些缺陷，如：GM(1,1)模型适用范围受限，仅限于完全等时距序列；灰色建模过程中背景值构造采用基本的紧邻均值法，当序列变化急剧时预测误差较大；旧数据的价值会随灰色系统的不断发展而降低，导致模型精度逐渐降低。

为解决传统GM(1,1)模型背景值构造所存在的缺陷，国内外研究者采用了许多方法。如：文献[6-8]的作者分别利用线性插值法、Newton-Cores公式及二次插值法等方法重构了背景值；文献[9-10]的作者提出将数据序列抽象为指数函数与非齐次指数函数，对GM(1,1)模型的背景值进行了研究。虽然上述方法取得了较高的精度，但也存在着一些问题，如：采用插值法构造背景值时，难以确定一个理想的n值；将数据序列抽象为函数法存在着表达形式复杂、计算繁琐等问题。鉴于此，笔者引用加权因子优化背景值构造，同时结合新陈代谢模型，建立改进的不等时距灰色GM(1,1)模型(简称MUGM(1,1,λ)模型)，以期实现对车辆冷却系典型金属腐蚀速率的精准预测。

1 改进不等时距GM(1,1)模型的建立

1.1 不等时距GM(1,1)模型

灰色GM(1,1)模型的建立实质，就是通过对原始数据的生成处理减弱其随机性，而得到易建模的新序列，然后利用曲线拟合得到系统的微分动态模型，最后对所建模型还原，得到所需的预测模型[11]。不等时距GM(1,1)模型(简称UGM(1,1)模型)是以GM(1,1)模型为基础建立而成，其模型建立步骤如下：

1) 确定原始数据序列。设原始数据序列为

{x(0)(ti),i=1,2,…,n}= {x(0)(t1),x(0)(t2),…,x(0)(tn)}，

(1)

式中：Δti=ti-ti-1，为时距，其值不为常数。

2) 确定原始数据的1-AGO序列。将时距作为乘子，对原始数据序列{x(0)(ti),i=1,2,…,n}进行一次累加生成，得到1-AGO序列

{x(1)(ti),i=1,2,…,n}= {x(1)(t1),x(1)(t2),…,x(1)(tn)}，

(2)

式中：

3) 建立白化方程。若原始数据序列{x(0)(ti),i=1,2,…,n}满足准光滑条件，而1-AGO序列{x(1)(ti),i=1,2,…,n}具有指数规律，则可对1-AGO序列{x(1)(ti),i=1,2,…,n}建立UGM(1,1)模型，其白化形式的微分方程为

(3)

式中：a为发展系数；u为灰色作用量。将微分方程(3)离散化，可得

x(0)(ti+1)+az(1)(ti+1)=u，

(4)

式中：

(5)

即{z(1)(ti+1)，i=1,2,…,n}为{x(1)(ti)，i=1,2,…,n}的紧邻均值生成序列。

4) 模型求解。由最小二乘法(a,u)T=(ATA)-1ATBn确定参数a、u的值。由

(6)

Bn=(x(0)(t2),x(0)(t3),…,x(0)(tn))T，

(7)

得到时间响应式

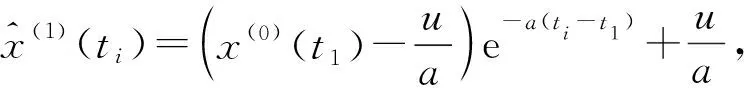
(8)

再将式(8)累减还原，得到原始数据的预测模型，为

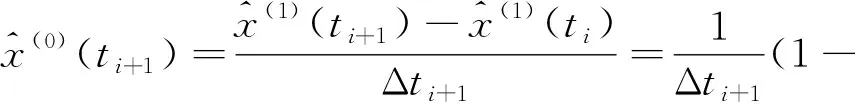
(9)

1.2 不等时距GM(1,1)模型的改进

不等时距GM(1,1)模型采用紧邻均值法进行背景值构造，但这种构造方式难以体现背景值在建模中的作用，且不适用于变化急剧的序列。此外，随着时间的推移，腐蚀过程往往容易受到一些随机扰动因素的影响，使得旧数据的信息意义逐渐降低，因此必须及时更新信息，以准确反映系统即时特征与趋势。为此，将背景值优化与新陈代谢模型相结合，对不等时距GM(1,1)模型进行改进，其步骤如下：

1) 在原模型基础上引入加权因子λ，以优化背景值构造，即将式(5)替换为

z(1)(ti+1)=λx(1)(ti+1)+(1-λ)x(1)(ti)。

(10)

其中，λ的值可通过满足原始值与预测值之间的最小平均相对误差来确定，其平均相对误差

(11)

2) 结合新陈代谢模型[12-13]，构建MUGM(1,1,λ)模型，具体实现步骤如下：

(1) 选取原始数据序列作为初始建模序列，即{x1(0)(ti)，i=1,2,…,n}={x(0)(t1),x(0)(t2),…,x(0)(tn)}。取x(1)(t1)=x(0)(t1)，按式(10)构建背景值，建立UGM(1,1,λ)模型。

依此类推，直到获得所求预测值。

1.3 MUGM(1,1)模型的精度检验

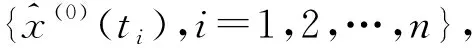
(12)

原始数据序列平均值

(13)

第ti时刻残差值ε(ti)的平均值

(14)

原始数据的标准差

(15)

残差的标准差

(16)

小误差概率

(17)

后验差比值

(18)

以上给出了检验模型精度的2个参数C、p，它们都是通过对残差考察来检验模型精度的。其中：p越大、C越小，说明模型预测精度越高、效果越好。利用这2个参数判定所得模型的精度，如表1所示。

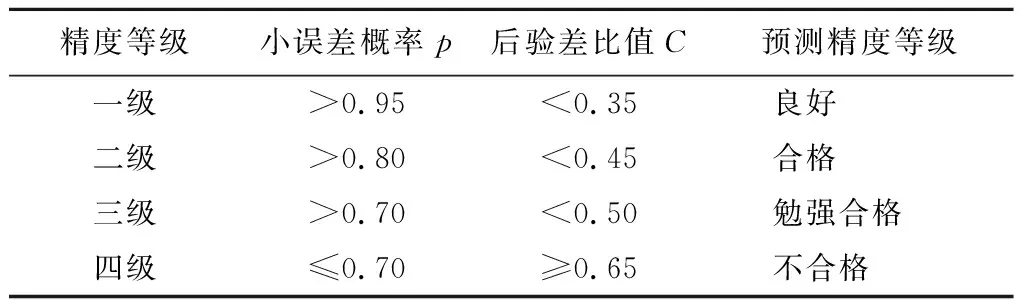
表1 模型精度等级

2 实例分析

表2为某型车辆装备冷却系用铜合金在模拟冷却系腐蚀环境下所测得腐蚀失重量。

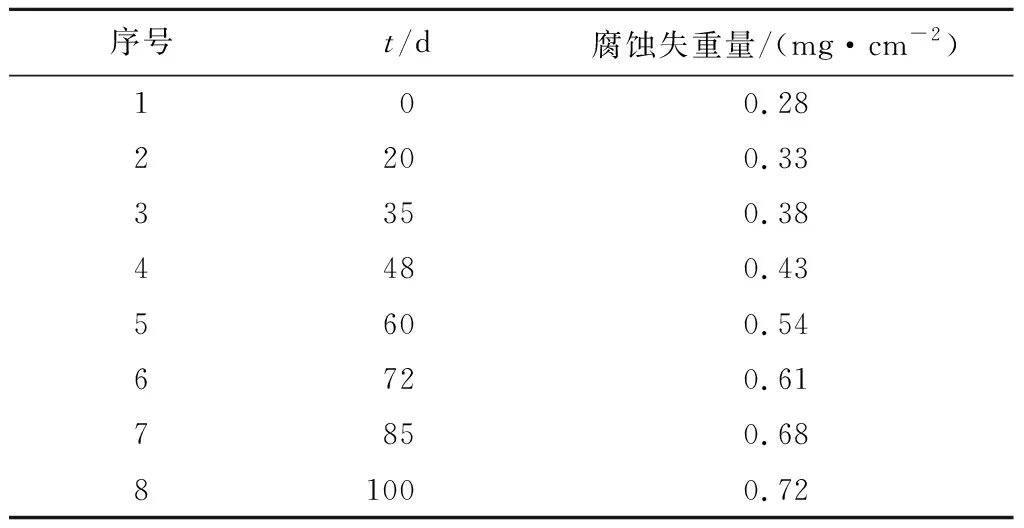
表2 冷却系用铜合金在模拟冷却系腐蚀环境下 所测得腐蚀失重量

2.1 MUGM(1,1,λ)模型的构建与求解

根据不同长度序列建立UGM(1,1)模型，对原始数据进行筛选，得到每次筛选序列的预测值与实际值的平均相对误差，进而确定一个最优的建模序列长度，具体数据见表3。可以看出：当建模序列长度为5时，其平均相对误差最小，为3.79%。因此，对表2中前5个实测数据进行数学建模，而后3个实测数据用于精度检验。

表3 不同长度序列的平均相对误差

设{x(0)(ti)}为冷却系用铜合金的腐蚀失重量，根据前面所叙述的建模方法对原始数据进行处理，得到传统UGM(1,1)模型的灰参数(a,u)T=(-0.011 5,0.276 0)。MUGM(1,1,λ)模型的计算过程如下：

2.2 模型精度检验

对传统UGM(1,1)模型和MUGM(1,1,λ)模型进行精度检验，结果如表4所示，其预测曲线与相对误差变化曲线分别如图1、2所示。由表4可以看出：2个模型的后验差比值分别为0.229 0、0.108 6，小误差概率均为1，即模型精度为一级，预测精度良好；与传统UGM(1,1)模型相比，MUGM(1,1,λ)模型的平均相对误差较低，为2.52%，这说明引入加权因子对背景值进行优化，可使MUGM(1,1,λ)模型预测的平均相对误差保持最小。

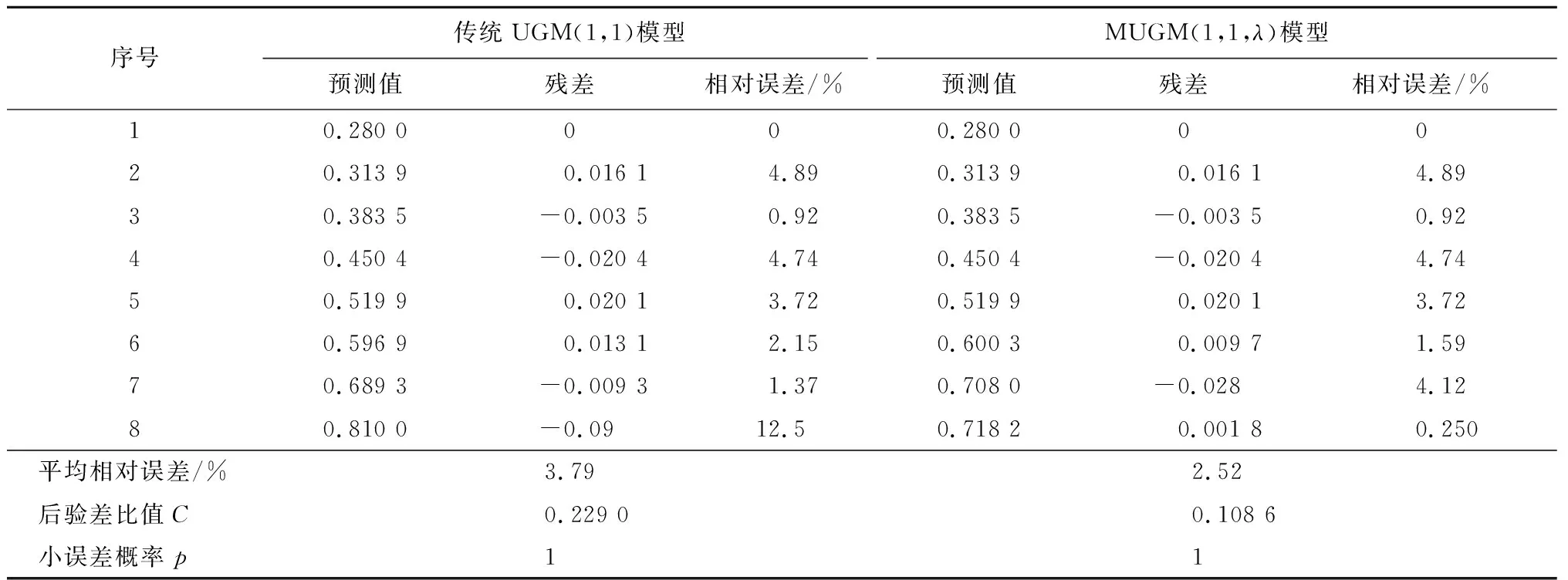
表4 模型预测值及精度检验结果

由图1、2可以明显看出：当铜合金在模拟冷却系腐蚀环境下100 d时，传统UGM(1,1)模型预测相对误差达到了12.5%，该数值远大于改进后的MUGM(1,1，λ)模型，说明传统UGM(1,1)模型不适合中长期预测,而MUGM(1,1，λ)模型则适合。

车辆装备冷却系用金属的腐蚀是一个长期、不确定的过程，随着时间的推移，该过程很可能受到一些新的腐蚀或抗腐蚀因子的影响。因此，采用MUGM(1,1,λ)模型可有效提高预测精度，并准确反映冷却系金属腐蚀实际状况。

3 结论

在传统UGM(1,1)模型的基础上，针对背景值构造所存在的缺陷，引入新陈代谢思想，建立一种改进的不等时距灰色预测模型MUGM(1,1,λ)，并运用该模型对车辆装备冷却系金属腐蚀进行预测，与传统UGM(1,1)模型相比，其所得预测值的平均相对误差较小，只有2.52%，同时具有较好中长期预测能力，可以实现对冷却系金属腐蚀的准确、高效预测。