基于VMD多尺度熵和ABC-SVM的装甲车辆识别

樊新海， 石文雷， 张传清

(陆军装甲兵学院车辆工程系， 北京 100072)

在新型作战体系下，对地面战场目标(如坦克、装甲车等)的准确识别是近距离作战中赢得信息优势和战场控制权的有效手段，在现代战争中有着重要的军事价值[1]。被动声识别也称为被动式声雷达，与传统雷达探测技术相比，有着抗干扰、低功耗、不易被发现等优点，可以弥补雷达低空探测盲区这一不足[2]。

噪声信号的特征提取和分类是装甲车辆声识别的主要环节，装甲车辆的噪声信号具有非线性、非平稳的特性，其特征提取与识别方法可以借鉴语音识别。孙国强等[3]将语音信号的特征梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients，MFCC)作为装甲车辆噪声信号的特征，通过分类实验证明了MFCC能够有效提取出装甲车辆噪声信号的特征信息，但其特征维数较高，运算量较大。笔者等[4]将噪声信号经验模态分解(Empirical Mode Decomposition，EMD)后提取的能量比作为特征向量，并将支持向量机(Support Vector Machine，SVM)作为分类器，实现了对4种装甲车辆的识别。EMD分解过程中存在模态混叠的现象，这会给特征提取带来一定的误差。同时，分类器SVM的核心参数均采用经验值，无法实现最高的识别率。

鉴于此，笔者将装甲车辆噪声信号模态分解得到的本征模态函数(Intrinsic Mode Funation,IMF)进行多尺度模糊熵(Multi-scale Fuzzy Entropy,MFE)计算,得到多尺度模糊熵特征，并将利用优化算法得到的支持向量机模型用于装甲车辆的声识别，对比并分析识别结果，进而得到最优模型。

1 目标声信号的获取与特性分析

以典型的4种履带式装甲车及3种坦克为识别对象，主要采集车辆原地发动(静止工况)和在正常路况下行驶(行驶工况)产生的排气噪声信号，以及夹杂履带与地面的冲击噪声信号，采集距离为3～5 m。根据装甲装备特点可知：坦克以及履带式装甲车的动力装置均为四冲程内燃机，发动机排气噪声爆发频率f与发动机转速n具有如下关系[5]：

(1)

式中：z为发动机气缸数。

在信号采集过程中，坦克及装甲车的最高转速均不超过3 000 r/min，结合式(1)可知其排气噪声理论爆发频率在几百赫兹范围内。装甲车辆行驶时产生的履带冲击噪声频带较宽，一般<4 kHz。结合以上因素，将噪声信号的采集参数设置为：采样频率8 kHz；采样点数32 768；采样时间4.096 s。

根据车辆的具体行驶状况，采集每种车型多种工况下的噪声信号，其噪声采集车型及其工况如表1所示。其中：高转速为1 300～1 600 r/min，中转速为1 000～1 300 r/min，低转速为800～1 000 r/min。

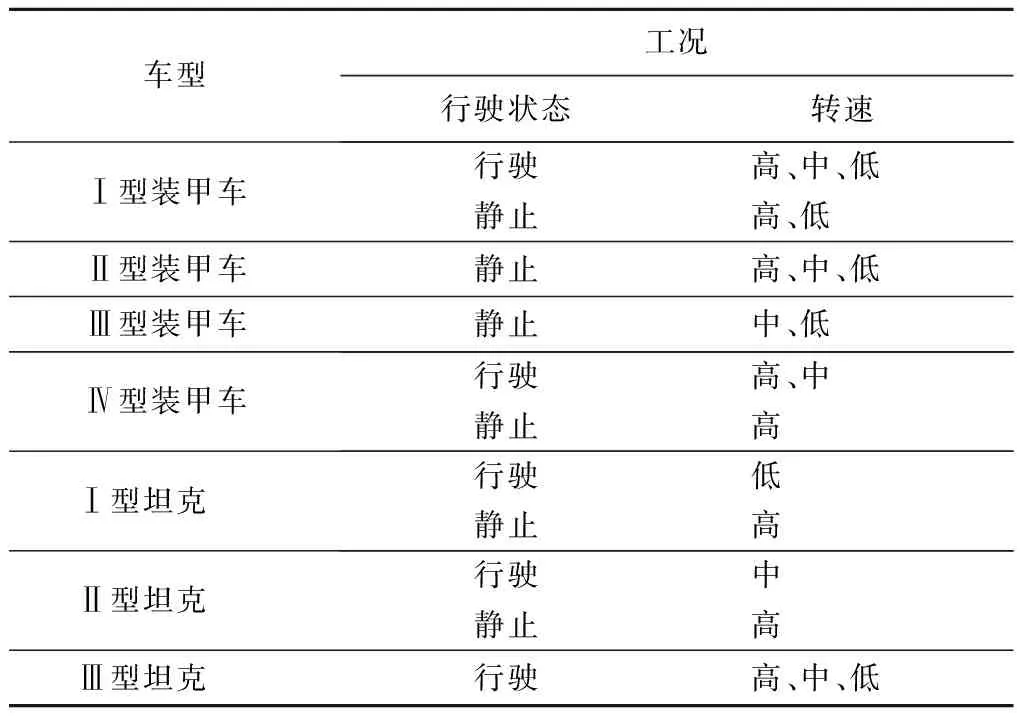
表1 噪声采集车型及其工况

将采集的噪声信号进行频谱分析，图1、2分别为Ⅰ型装甲车和Ⅱ型坦克的目标噪声信号及其功率谱。可以看出：噪声主要能量均集中在<1 000 Hz的低频段。由于噪声信号在低频段具有明显差异性，这一特点可以作为分类的关键依据。

2 噪声信号的VMD-MFE提取

2.1 VMD原理

变分模态分解[6](Variational Mode Decomposition，VMD)是一种自适应信号处理方法，其在EMD和局部均值分解(Local Mean Decomposition，LMD)基础上有效减少了模态混叠现象，具有较好的理论基础。VMD实质上是多个自适应Wiener滤波组，具有更好的鲁棒性[7]。VMD整体框架是变分问题，根据预设模态分量个数对原始信号p进行分解,得到本征模态函数。

VMD变分模型为

(2)

式中：{uk}={u1,u2,…,uK}，为分解得到的K个模态分量；{ωk}={ω1,ω2,…,ωK}，为各模态分量中心频率；∂t表示对t求偏导运算；δ(t)为单位脉冲函数。

利用交替方向乘子法(Alternate Direction Me-thodof Multipliers，ADMM)可得到各模态分量在频域内的更新表达式，为

(3)

同样，在频域对中心频率求解，得到ωk的更新表达式为

(4)

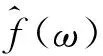
2.2 多尺度模糊熵

多尺度熵(Multi-Scale Entropy，MSE)是指不同尺度的样本熵，其从不同尺度衡量时间序列的复杂性，克服了传统的基于单一尺度样本熵的缺陷，能反映时间序列更深层的模式信息[8]。模糊熵(Fuzzy Entropy，FE)[9]采用指数函数代替单位阶跃函数，克服了相似性度量的突变，能更好地突出信号间的差异。因此，以模糊熵替换样本熵，得到多尺度模糊熵，其计算步骤如下：

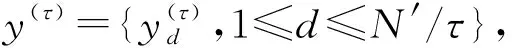
(5)

式中：τ为尺度因子，一般为正整数。

2) 计算各尺度因子下粗粒化序列的模糊熵，其计算公式为

MFE(X,τ,m,r)=FE(y(τ),m,r)。

(6)

式中：m为嵌入维数；r为相似容限。

2.3 VMD-MFE提取步骤

在处理非线性信号时，常将时频信号处理方法与多尺度熵相结合而得到多尺度熵的特征值。与未经处理的原始时频信号相比，该特征值更能体现时频信号的特征。将装甲车辆噪声信号先进行VMD分解，对分解得到的IMF时间序列X进行粗粒化处理，并提取多尺度模糊熵，得到多尺度模糊熵特征(VMD-MFE),其具体步骤如图3所示。

3 人工蜂群算法优化的支持向量机

3.1 人工蜂群算法

人工蜂群(Artificial Bee Colony，ABC)算法是一种模拟蜂群采蜜过程的群体智能算法[10]。引领蜂、跟随蜂和侦察蜂为3种不同工种，它们会根据各自分工协同完成采蜜过程各阶段任务，并实时收集和共享蜜源，从而找到最佳蜜源的位置。

3.2 ABC-SVM

研究[11]表明：SVM作为分类器使用时，误差惩罚因子C和核函数参数g是其分类性能的主要影响因子。以径向基为核函数的SVM，利用人工蜂群算法对C和g进行参数寻优，其优化过程如下：

1) 初始化参数。设置SVM中C和g的搜索范围，在搜索范围内随机产生N组C和g，则第n个初始蜜源位置为Xn(n=1,2,…,N)；同时，初始化蜂群数量、蜜源被开采次数以及同一蜜源被开采极限。

2) 引领蜂产生蜜源。在蜜源附近，引领蜂按照

Vn=Xn+rand(-1,1)·(Xn-Xk′)

(7)

随机产生新蜜源并开展邻域搜索。式中：Vn为新产生的第n个蜜源位置；k′=1,2,…,N，为随机指定个体，且k′≠n。

3) 跟随蜂选择蜜源。跟随蜂到达蜜源后，同样按照式(7)对蜜源进行一次邻域搜索，并依照

(8)

选择蜜源。式中：Pn为第n个蜜源被选择的概率；Fn为第n个蜜源的适应度，也就是蜂群算法的寻优目标，在此指蜜源坐标代入SVM得到分类准确率。

4) 放弃蜜源重新搜索。规定蜜源最大采集次数为M，当采集次数>M而仍未找到最优值时，放弃蜜源，并将与该蜜源对应的引领蜂转换为侦察蜂，按照

Xi=Xmin+rand(0,1)·(Xmax-Xmin)

(9)

产生新蜜源并重新搜索：否则，转到步骤2)。式中：Xmax和Xmin分别为搜索空间的上限和下限。

5) 判断是否满足最大迭代次数。若满足，则跳出循环，输出结果；否则，转到步骤2)。

4 实验及分析

4.1 特征提取实验

从每种车型采集的原始信号中截取长度为1.024 s的信号，作为特征提取的样本信号。由于VMD算法相当于自适应维纳滤波器组，当模态分量个数较少时，原始信号中的一些重要信息将被滤掉丢失；当分解模态分量个数较多时，相邻模态分量的中心频率则会相距较近，容易产生频率混叠。因此，在对样本信号进行VMD分解前，要先确定模态分量个数K。以I型装甲车为例，对其样本信号进行VMD分解，不同K值对应的中心频率如表2所示。可以看出：当K=6时，中心频率1 646、1 938 Hz相接近，可能会出现模态混叠。因此，选K=5较为合适。

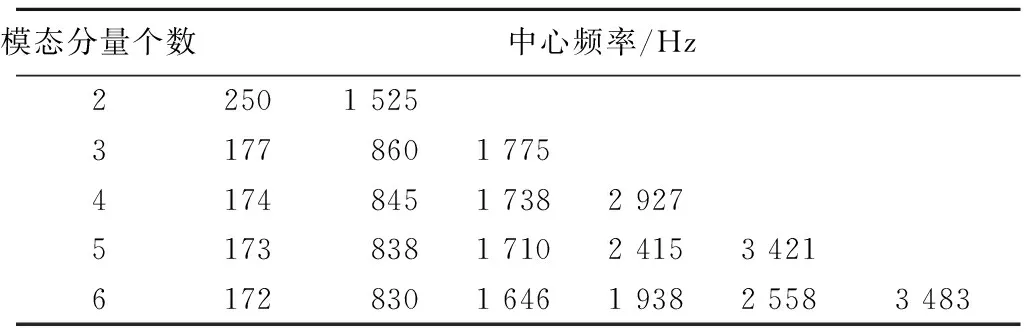
表2 不同K值对应的中心频率

VMD分解中的另一个影响因素是惩罚参数a。为保证VMD分解过程中具有较好的去噪能力和细节保留度，取a=1 000。以Ⅰ型装甲车静止、高转速条件下的样本信号为例进行VMD分解，产生的5个IMF分量如图4所示。

计算各个模态MFE的值，其中嵌入维数m与样本数据长度有关，一般样本数据越长，m越大。本文中噪声样本信号点数为 8 192，参考文献[12]，取m=2；一般取相似容限r=(0.15～0.25)δ，其中δ为原始样本的标准差。尺度因子会影响特征维数：若特征维数过小，则不足以体现样本的特征；若特征维数过大，则会造成分类耗时过长。因此，本文取τ=3。综上考虑，VMD-MFE方法提取的特征维数为15。

为了验证VMD分解的优越性，分别对样本信号进行EMD和集合经验模态分解(Ensemble Empiri-cal Mode Decompostion,EEMD)分解，并将分解模态的MFE值作为特征向量。由于EMD和EEMD需要多层分解，若计算所有模态的MFE值，则运算量较大。为保持与VMD分解过程的一致性，取2种分解结果的前5个模态，计算得到的15维EMD-MFE和EEMD-MFE变化曲线如图5所示。可以看出：当装甲车型号不同时，与基于EEMD-MFE和EMD-MFE方法相比，基于VMD-MFE方法得到的噪声信号特征值的差异性较大，说明经VMD分解得到的5个模态的多尺度模糊熵可区分度较高，而经EEMD和EMD分解得到的多尺度模糊熵的可区分难度较低。这也说明VMD分解较好地克服了EMD和EEMD分解中存在的模态混叠现象。

4.2 噪声分类实验

4.2.1 特征筛选

将SVM作为分类器，用以分析3种特征值对装甲车辆噪声识别准确性及分类时间的影响。每种车型分别从3种特征值中取150组样本作为训练集，100组样本作为测试集，每种特征值的训练集总样本数为1 050，测试集总样本数为700。根据经验，取惩罚因子C=80，核函数参数g=2。将选取的数据集输入到SVM中进行分类实验，其识别结果如表3所示。可以看出：当识别时间相同时，与EMD-MFE和EEMD-MFE相比，以VMD-MFE为特征值的SVM识别率较高，说明VMD具有更好的自适应能力，能够有效地分离出噪声信号中的特征量。因此，选择VMD-MFE作为装甲车辆噪声识别的特征值。

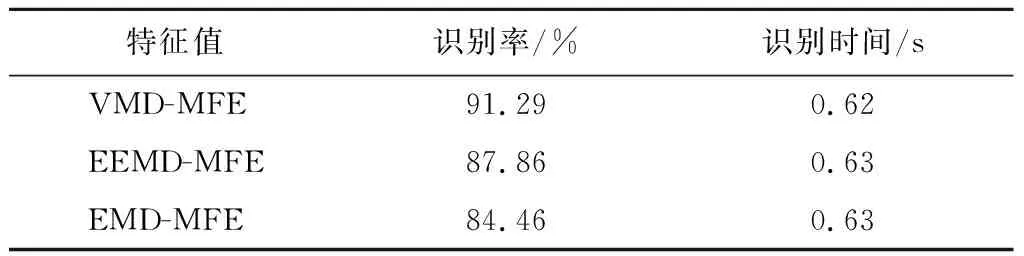
表3 3种特征值识别结果

4.2.2 算法优化结果分析

采用引力搜索算法(Gravitational Search Algorithn,GSA)、ABC算法和布谷鸟搜索(Cuckoo Search,CS)算法三种群智能优化算法对SVM进行优化，迭代次数均为30次，得到参数优化的分类器模型GSA-SVM、ABC-SVM、CS-SVM。将VMD-MFE分别输入到3种模型中进行识别实验并对比，其误差率随迭代次数的变化趋势如图6所示。可以看出：与GSA、CS算法相比，ABC算法在参数寻优的过程中具有最快的收敛速度，其在第6代就达到了最低分类误差率5.85%。这说明在以VMD-MFE为特征值时，ABC算法对SVM的优化效果最好。

表4和图7分别为4种分类器模型识别结果对比和ABC-SVM的分类结果。可以看出：与GSA-SVM、CS-SVM相比，ABC-SVM分类器模型具有更高的识别率，总体识别率达到了94.14%；与SVM相比，以ABC-SVM为分类器模型时对Ⅰ、Ⅱ型坦克的识别率有显著提高。上述结果说明：ABC算法对SVM的核心参数具有良好的寻优能力，能够得到使SVM达到最优识别率的参数组合。

表4 不同分类器模型识别结果 %

5 结论

笔者建立了一种以VMD多尺度熵为特征值，以ABC算法优化的SVM为分类器的装甲车辆噪声识别模型，其总体识别率达到94.4%，具有较好的识别效果。实验分析结果表明：以VMD-MFE为特征值的识别率较高，说明VMD分解效果优于EMD和EEMD；ABC的参数寻优效果优于GSA和CS算法，具有较快的收敛速度和较强的寻优能力。

为了提高装甲装备声识别的应用可行性，下一步应丰富不同车型的噪声样本库，并对3种算法优化效果进行深入对比分析，以对ABC算法进行改进，并进一步提高装甲车辆声识别准确率。