带交错影响的Gray-Scott系统的分岔研究
李红燕
(陆军装甲兵学院基础部, 北京 100072)
Gray-Scott系统是一个典型的反应扩散系统,它能展现出丰富的动力学行为,尤其在一定参数范围内可展现出混沌行为,因此受到广泛关注。Gray-Scott系统描述的是2种化学物质参与化学反应的过程[1],可由以下非线性反应扩散方程组表示:
(1)
Gray-Scott系统可以反映2种化学物质在反应中的基本规律,但VANAG等[2]提出交错扩散影响是化学反应中不容忽视的因素,因此需要考虑物质u的梯度对物质v产生的交错扩散影响。带交错扩散影响的Gray-Scott系统可由如下偏微分方程组描述:
(2)
式中:d0为交错扩散系数。
虽然Gray-Scott系统是一个简单系统,但PEARSON[1]发现其可以展现出各种模式,由此引发众多学者对Gray-Scott 系统模式生成及各种解的稳定性进行研究[3-10]。MAZIN等[10]采用线性稳定性分析方法,在研究平衡点稳定性的基础上,研究了Gray-Scott模型远离平衡态的斑图形成机制,通过对初值的剧烈扰动获得了各种模式解,给出了时空混沌模式参数和初值的选取方法。NISHIURA等[11]在分岔分析的基础上研究了在Gray-Scott模型中出现的时空混沌行为。虽然上述结果为后续Gray-Scott系统及其推广系统研究提供了理论和方法基础[12-17],但目前对带交错影响的Gray-Scott 系统稳定性的相关研究鲜见报道。因此,笔者利用线性稳定性方法研究带交错影响的Gray-Scott系统的平衡点及其稳定性,并对系统的分岔情况进行研究。
1 带交错影响的Gray-Scott系统平衡点的稳定性和分岔情况
求解方程组
可得带交错影响的Gray-Scott系统有3个常值平衡点,其中包括1个平凡平衡点E0=(u0,v0)=(1,0),而当d≡1-4(a+b)2/a>0时,出现2个非平凡平衡点,分别为
(3)
(4)
说明系统(2)与系统(1)有3个相同的平衡点。
利用线性稳定性方法分析各平衡点的稳定性[10]:由于系统(2)与系统(1)的线性近似系统相同,因此平衡点具有相同的稳定性,即系统(2)在E0点处总是稳定的,在E2点处总是不稳定的,在平衡点E1处可能稳定,也可能不稳定。
由于在讨论鞍结点分岔和霍普夫分岔性质时不考虑系统的交错影响,因此系统(2)与系统(1)有相同的鞍结点分岔和霍普夫分岔情况。
鞍结点分岔线为
(5)
当a和b满足不等式
霍普夫分岔线为
(6)
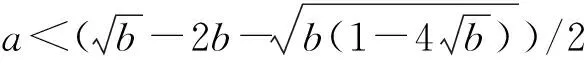
2类不稳定的公共区域可表示为
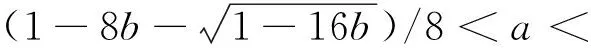
(7)
2 带交错影响的Gray-Scott系统的图灵分岔
2.1 带交错影响的Gray-Scott系统图灵分岔线的解析求解
图灵分岔的必要条件是:在不考虑扩散项时,系统对均匀微小扰动是稳定的;当加入扩散项时,系统对小的空间扰动是不稳定的[10]。考虑E1的图灵稳定性,参照文献[10]中的方法和结果,系统(2)的线性微扰方程表示如下:
(8)
式中:
(9)
将微扰变量在傅里叶空间展开,根据线性稳定性分析方法[10],得到系统(2)的特征方程为
λ2-Tλ+D=0,
(10)
式中:
T=a11+a22-q2(d1+d2),
(11)
D=a11a22-a12a21-q2(a22d1+
a11d2-a12d0)+q4d1d2,
(12)
其中q为微扰参量。
特征方程(10)的特征值为
将u1和v1代入式(9)、(11)、(12),可得
Dmin= (a+b)(v2-a)-[d1(a+b)+
2d0(a+b)-d2(v2+a)]2/(4d1d2)<0。
即
[σ(a+b)+2σ1(a+b)-(v2+a)]2>4σ(a+b)(v2-a)。
(13)
式中:σ=d1/d2;σ1=d0/d2。
则系统(2)的图灵分岔线可表示为
[σ(a+b)+2σ1(a+b)-(v2+a)]2= 4σ(a+b)(v2-a)。
(14)
由文献[10]可知:Gray-Scott系统的图灵分岔线为
在图灵线下方区域内,即参数满足
[σ(a+b)-(v2+a)]2>4σ(a+b)(v2-a)
(15)
时,平衡点E1是图灵不稳的。
由式(14)和(15)可知:交错扩散系数d0会影响σ1,从而使得两系统图灵分岔线的位置不同。
2.2 带交错影响的Gray-Scott系统图灵分岔线的位置分析
当图灵分岔线在鞍结点分岔线和霍普夫分岔线之间时,其交叉作用会使系统显示出丰富的性态,因此,将参数首先限定在此区域中对比系统(1)和系统(2)图灵分岔线的位置。为便于叙述主要结果,先给出以下2个引理。
引理1:若参数a>0和0 (a+b)4>a2b。 (16) 引理2:若参数a>0和0 2(a+b)3-a2>0。 (17) 以下为本文的主要结果,其揭示了Gray-Scott系统和带交错影响的Gray-Scott系统的图灵分岔线之间的位置关系。 定理1:若σ≥1,σ1>0,参数a>0,0 证明:设f=σ(a+b)-(v2+a),将式(3)中的值代入,可得 由条件σ≥1可得 σ(a+b)+2σ1(a+b)-(v2+a)>σ(a+b)-(v2+a), (18) 由于不等式(18)两边均大于0,因此对其两边进行平方可得 [σ(a+b)+2σ1(a+b)-(v2+a)]2> [σ(a+b)-(v2+a)]2, (19) 由不等式(7)和(19),可得此时参数a和b满足不等式(13),定理1得证。 由定理1可知:当σ≥1,σ1>0时,带交错影响的Gray-Scott系统的图灵分岔线比Gray-Scott系统的图灵分岔线更靠近霍普夫分岔线。 σ=2时,σ1=0.1,0.3下Gray-Scott系统和带交错影响的Gray-Scott系统不同分岔线的位置分别如图1、2所示。可以看出:当σ≥1,σ1>0时,带交错影响的Gray-Scott系统的图灵分岔线比Gray-Scott系统的图灵分岔线更靠近霍普夫分岔线;当σ1变大时,带交错影响的Gray-Scott系统的图灵分岔线会远离Gray-Scott系统的图灵分岔线,与定理1结果一致。 定理2:若σ≥1,σ1<0,2|σ1|(a+b)<2[σ(a+b)-(v2+a)],且参数a>0,0 证明:由定理1的证明过程可知f=σ(a+b)-(v2+a)>0,当σ1<0,且2|σ1|(a+b)<2[σ(a+b)-(v2+a)]时,有 [σ(a+b)+2σ1(a+b)-(v2+a)]2< [σ(a+b)-(v2+a)]2。 (20) 由不等式(13)和(20),可得此时参数a和b满足不等式(15),定理2得证。 由定理2可知:当σ≥1,σ1<0时,带交错影响的Gray-Scott系统的图灵分岔线比Gray-Scott系统的图灵分岔线更靠近鞍结点分岔线。图3为σ=2时不同分岔线的位置,可以看出:当σ=2,σ1=-0.2时,带交错影响的Gray-Scott系统的图灵分岔线在Gray-Scott系统的图灵分岔线下方,更靠近鞍结点分岔线,与定理2结果一致。 由本节分析可知:加入交错扩散可改变夹在Gray-Scott系统的图灵分岔线和霍普夫分岔线之间区域的面积,而由文献[10]可知,在这个区域内Gray-Scott系统可呈现出混沌模态,因此有必要通过数值模拟进一步分析带交错影响的Gray-Scott系统在这个区域内的模态。 采用欧拉法研究带交错影响的Gray-Scott系统的时空发展行为,并与Gray-Scott系统进行对比分析。空间变量x的步长Δx=0.01,时间变量t的步长Δt=0.01,初始条件(u0,v0)T=(1,0)T,并伴随中间的剧烈震荡。扩散系数d1=2×10-5,d2=10-5,其他参数在每次模拟时取值不同。 图4、5分别为Gray-Scott系统和带交错影响的Gray-Scott系统的解u(x,t)在不同参数a、b下的时空发展图。对比图4(a)、(b)以及图5(a)、(b)可以看出:当d0>0时,加入交错扩散可使Gray-Scott系统解的振荡混乱程度减弱,这种效果在图4(a)、(b)的对比中尤其明显,加入交错扩散使原本的混沌运动变为规则运动。对比图4(a)、(c)以及图5(a)、(c)可以看出:当d0<0时,加入交错扩散可使Gray-Scott系统解的振荡混乱程度加强,这种效果在图5(a)、(c)的对比中尤其明显,加入交错扩散使原本的规则运动变为混沌运动,当参数在Gray-Scott系统的图灵分岔线和霍普夫分岔线之间的区域取值时,通过大量的数值模拟都发现了同样的规律,但要注意此时|d0|要足够小。 笔者采用线性稳定性方法研究了带交错影响的Gray-Scott系统的平衡点及其稳定性,结果表明:交错扩散不影响系统的平衡点及鞍结点分岔和霍普夫分岔特性。采用微扰法研究了交错扩散对带交错影响的Gray-Scott系统图灵分岔线的影响,结果表明:交错扩散会影响带交错影响的Gray-Scott系统的图灵分岔线位置,而且当交错扩散系数为正时,带交错影响的Gray-Scott系统图灵分岔线更靠近霍普夫分岔线;当交错扩散系数为负且绝对值足够小时,带交错影响的Gray-Scott系统图灵分岔线将会远离霍普夫分岔线。通过数值模拟分析发现:加入交错影响可使Gray-Scott系统解的振荡混乱程度加强或减弱。研究结果为更进一步的系统模式分析奠定了基础。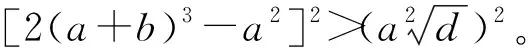
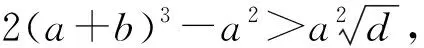
3 数值模拟分析
4 结论

