基于SAW-DPDP方法的ad hoc网络节点重要性分析

谭 冕， 赵 静

(陆军勤务学院军事物流系， 重庆 401331)

节点重要度的排序具有重要意义，因为无线ad hoc网络节点的拓扑结构不同，重要度大的节点能够在更大程度上影响网络的结构与功能，优先对重要度大的节点进行攻击，会导致网络性能下降更快，故蓄意攻击通常按照节点重要度进行排序，并按由大到小的顺序进行攻击。对节点重要度的研究有利于保护网络，并提高网络的抗毁性，这在战场或其他恶劣的通信环境中显得尤为重要。由于实际应用的迫切需求，节点的重要度排序问题已成为研究热点。

任卓明等[1]基于节点度和聚集系数等局部信息对网络节点进行了重要性度量分析，仿真实例证明了此方法对大规模网络的有效性；于会等[2]提出了“逼近立项排序法”的多属性决策方法，利用节点的多个指标对节点的重要性进行度量，并将其数值作为节点的属性，其具有良好的扩展性；韩忠明等[3]为解决面向结构洞节点的节点排序问题，采用基于ListNet的排序学习方法吸收网络约束系数、效率、PageRank值等7个度量指标，选择出的节点具有较高的传播能力；段东立等[4]建立了一个可调负载重分配级联失效模型，以此提出考虑级联失效局域信息的节点重要性指标，并重点分析了动力学特征下节点的演化机理；刘建强等[5]提出了基于节点疏远方法来评价网络节点重要性，该方法合理疏远了节点的关联边，并选择能体现全局和局部信息的通信效率和聚集系数作为度量。

上述研究都是基于网络所有节点的重要性进行分析的，并没有考虑会造成ad hoc网络分割的关键节点[6]。由于ad hoc网络中的拓扑结构具有不确定性，有的节点度大，有的节点是“桥梁”节点，有的节点处于中间位置，因此单一的评估方法无法合理评估节点对网络拓扑结构的影响。为了准确判断节点的重要性，笔者针对现有的一些重要性评价指标不够全面的缺点，先用简单加权(Simple Additive Weighting，SAW)的方法整合节点的度、聚集系数等局部信息，以及介数中心性、接近中心性等全局信息，然后用分布式分割探测算法(Distributed Partition Detection Protocol，DPDP)判断网络中存在的关键节点，通过对节点重要性的综合排序有效判断对拓扑贡献更大的节点。

1 方法

1.1 基于节点重要度排序的抗毁性攻击策略

通信网络节点面对的攻击方式有随机攻击(Random Attack,RD)和蓄意攻击2种。其中：随机攻击是指敌方不能获知我方通信网络精确信息时进行的攻击，这种节点攻击方式具有随机性，成本高且效率低，尤其是以ad hoc网络形式组网时，分布式的结构能够有效应对随机攻击；蓄意攻击是指敌方可以获取相对精确的节点信息，并能够以一定的攻击策略对节点实施的攻击行为，相对于随机攻击，其效果更明显，依据收集的通信节点拓扑信息的多少，可以分为局部信息下的蓄意攻击和全局信息下的蓄意攻击。

1.1.1 局部信息下的蓄意攻击策略

如果敌方只能获取通信节点的连边关系时，可选择度中心 (Degree Centrality,DC)[7]为指标发起攻击。在当前策略下，节点的重要性表现为中心性，意味着节点通过与其他节点连边数量的多少体现重要性，连边数量越多则越重要，对拓扑结构的影响力越大。

若当前网络存在任意节点i，其排序关系可用归一化度中心指标DC(i)来表示，其计算公式为

(1)

式中：Ni为节点i的邻居数；N为网络的节点数。

1.1.2 全局信息下的蓄意攻击策略

1) 基于节点介数方法的攻击策略。当敌方能够获取我方全局的拓扑信息时，可选择基于节点介数作为评估指标。介数中心性(Betweenness Centrality,BC)[8]认为：网络中经过一个节点的最短路径数越多，则这个节点就越重要，其排序关系可表示为

(2)

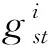
2) 基于节点接近中心性方法的攻击策略。当敌方能够获取节点与网络中其他节点平均距离的信息时，可选择基于节点接近中心性 (Closeness Centrality,CC)[9]的攻击策略。要使得节点i接近中心性CC(i)数值较大，则需使节点i与其他节点的平均距离di较小，其计算公式分别为

(3)

(4)

式中：dij为节点i和j之间的最短路径长度。

1.1.3 攻击策略流程

攻击策略流程如下：

1) 归类、分析掌握的搜救通信节点信息；

2) 选择具体的攻击策略和范围；

3) 根据是否有保护节点的措施和攻击的强度，判断节点是否失效；

4) 若节点失效，则删除该节点及连边；

5) 当攻击策略删除了网络所有节点或者当前攻击范围内的节点，则停止攻击，否则回到步骤2)。

1.2 考虑关键节点的攻击策略

假设图G=(V,E) 是一个双向的网络，其中V={v1,v2,…,vN}，是网络中所有节点vi(i=1,2,…,N)的集合，|V|=N;E={e1,e2,…,em}⊆V×V，是节点间边ej(j=1,2,…,m)的集合，|E|=m。

无线ad hoc网络节点在功能上是平等的，但存在部分节点对整个网络拓扑结构影响较大，如：作为2个独立子网唯一通道的节点，当该节点失效时，网络将分化成2个子网络，极大地影响网络连通性，此类节点可称为关键节点。介数中心性最大的节点有可能是关键节点，但上述攻击策略没有明确指出这类节点，敌方若能够检测出关键节点且加以攻击，则对网络拓扑结构造成更大的威胁；我方若对关键节点进行保护，则可以增强网络抗分割的能力。

1.2.1 基于SAW的节点重要性判断方法

SAW方法作为多准则决策(Multi-Criteria Decision-Making,MCDM)的重要方法之一，能够从多角度综合评估，进而为最优决策的选择提供参考。

分别选择局部和全局拓扑信息指标进行关键节点的检测。局部拓扑信息包括度中心性和聚集系数；全局拓扑信息包括介数中心性和接近中心性。其中：度中心性主要考虑节点影响邻居的数量，节点度越大，则该节点越重要；聚集系数主要考虑邻居节点间的可替代性，替代性越差，则地位越重要[10]；介数中心性认为网络中经过一个节点的最短路径数越多，则这个节点就更重要；网络中节点与其他节点的平均距离的倒数定义为接近中心性，其值越大，则意味着该节点的信息能更快地传播出去。

基于上述因素的考虑，通过SAW的方法融合度中心性、聚集系数、介数中心性和接近中心性这4个重要性属性，并通过在多因素之间的参数调节，最终得到想要的重要性数值，加权后的节点重要性为

NI(i)=k1[DC(i)×F(Ci)]+k2CC(i)+k3BC(i)，

(5)

式中：k1、k2、k3为调节权重，且k1+k2+k3=1，0≤k1,k2,k3≤1；Ci为节点i的聚集系数，其计算公式为

(6)

其中Ei为节点i与邻居节点间的连边数量；F(Ci)为Ci的函数，其计算公式为

F(Ci)=10-Ci。

(7)

1.2.2 基于DPDP的关键节点检测方法

在得到所有节点的重要性数值后，需要进一步分析网络的拓扑结构，找出ad hoc网络可能出现的关键节点。

关键节点的检测方法选择李建东等[11]提出的DPDP方法，即

Ni-Mi≥2。

(8)

式中：Mi为基本回路度，即节点i经过不同邻居节点对的基本回路总数。当节点i满足式(8)时，该节点就是关键节点。

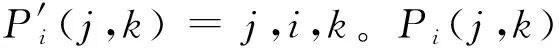
基本回路度Mi=∑Ci(j,k)。邻居节点对及基本回路如图1所示。

当计算出网络存在的关键节点后，需要对NI(i)进行如下修正：

(9)

式中：ω为附加值。

因为0≤NI(i)≤1，修正后关键节点会处于优先攻击的序列中。若同为关键节点，则会按照局部、全局拓扑信息分析出关键节点中最有价值的节点，故使用该攻击策略可以有效识别出ad hoc网络中关键节点的重要性，并按照顺序进行有效打击。

2 抗毁测度

无线ad hoc网络抗毁性是指节点遭到攻击后拓扑结构被破坏的难易程度，需要根据研究的内容合理选择抗毁性指标。本文假定由搜救人员组成的ad hoc网络遭受打击后信息传输无法得到保障，搜救活动受阻，故选择能够连通最大通信区域的连通系数和可以考察网络连通性好坏的网络效率作为抗毁性指标。

从通信网络的拓扑结构角度看，重要度高的关键节点很容易被优先列入打击目标。节点的重要性往往也体现在该节点被移除之后对网络的破坏性，因此为进一步比较节点间的重要性，通过删除节点的方法进行衡量。引入连通系数S作为抗毁测度，其计算公式为

(10)

式中：N′为最大连通片的节点数；N为初始节点数。仅考虑单点打击时，分别计算移除一定比例节点后网络的最大连通率。

为了方便对比，本文还选择了另一种衡量指标，即网络效率，用以表示网络连通性的好坏。如果网络中节点被删除后，则该节点与其邻居的联系也会断掉。假设当前网络进行节点删除操作后，节点i的信息仍然能够到达节点j，可能因为某些节点的删除，导致节点i到达节点j的最短路径长度dij增大，进而可以推测出整个网络的连通性可能有所降低，用1/dij表示节点i、j的连通效率，故网络效率可表示为

(11)

式中：G为最大连通图。

由式(11)可知：若ε=0，意味着网络中的节点全部是孤立节点；ε=1，代表网络连通性最好。本文通过删除的方法对比分析网络节点重要性攻击策略的优劣，需要计算网络没有遭受攻击时的效率ε0和删除了一定比例节点后的效率ε，则网络效率的下降比例

(12)

显然有，ε，e∈[0,1]。当e=1时，意味着网络效率为0；当e=0时，则网络效率不变。当e的数值逐步变大时，意味着网络效率逐步下降，以此可对重要性方法的准确性进行度量。

3 仿真分析

通过MALAB进行仿真，考察不同攻击策略对网络连通系数的影响和对网络效率下降比例的影响。

仿真的主要参数为：节点数N=36；节点删除比例del=0.1∶0.1∶0.9；通信半径R1=200，R2=100；仿真时长T=400；蒙特卡罗次数MC=50；关键节点附加值ω=1。仿真场景假设为500 m×500 m。通过合理选择不同的通信半径，使构建的ad hoc网络具有小世界网络的特性。移动模型选择基于关键位置的2D 随机游走移动模型[12](2D Random Walk with Key Localization,2D RWKL)，该移动模型会根据遇险人员的位置信息展开一定区域范围内的搜索行动，具有一定的真实性。

由于生成的网络模型具有随机性，因此最后得到的图形数据有一定的误差，为了更好地表现趋势，需要对得到的网络连通系数、网络效率下降比例进行拟合。结合图形的趋势，选择二阶多项式进行拟合，得到的和方差接近于0，具有较好的拟合效果。

3.1 不同攻击策略对网络连通系数的影响

图2为不同攻击策略对网络连通系数的影响，可见：随着删除比例的增加，网络连通系数近似于呈线性减小的趋势。同时，不管是哪种攻击策略，只要攻击掉了相应比例的节点，在计算连通效率时，若连通系数低于攻击比例，说明此时必然已经产生了“信息孤岛”节点。不同攻击策略对网络连通系数的影响顺序是：SAW-DPDP>BC>CC>DC>RD。

当删除比例为0.8、0.9时，不同攻击策略下网络连通系数的数值很接近，这是因为删除比例过高导致现存最大连通片内的节点数目很少，基本无法体现出不同方法的区别。

SAW-DPDP方法在仿真过程中，连通系数始终处于最低值，说明该方法能够有效得出节点的重要程度。随后按照得到的节点重要性排序进行攻击，相对于其他攻击策略，SAW-DPDP能够使连通系数最小，亦即将网络分成多个“信息孤岛”，且最大连通片包含的节点数最少，说明该方法有利于在这种场景中实现，可达到最佳效果，也验证了方法的有效性。

RD即随机攻击策略，由于ad hoc网络分布式的结构，其连通系数最高，故可以有效应对这种攻击方法。

基于DC、RD方法的攻击策略在连通系数上几乎保持一致的水准，这是因为完全以度为指标进行判断的局部拓扑方法在当前网络中不能体现出优势，因为每个节点的度数可能差距不大，且有多条路径存在的可能。

基于CC方法可以通过计算节点与网络中其他节点的距离表示重要性，而BC方法通过节点最短路径数量描述其重要性。由图2可知：BC的方法更适用于ad hoc网络，能够更精确地描述节点的重要性。

3.2 不同攻击策略对网络效率下降比例的影响

图3为不同攻击策略对网络效率下降比例的影响，可见：随着删除比例的增加，网络效率下降比例近似于呈线性增加的趋势;当删除比例为0.9时，网络效率下降比例接近于1，说明此时网络效率几乎为0，节点间的距离近似于无限大，当前网络全部是孤立节点，信息基本无法传递出去。不同攻击策略对网络效率下降比例的影响顺序是：SAW-DPDP>CC>BC>DC>RD。

随着删除比例的增加，SAW-DPDP方法始终对网络效能构成较大威胁，网络效率逐步下降，网络效率下降比例逐步增大，说明该方法相对于其他方法能够使最短路径长度增大最快。

CC方法在网络效率下降比例的影响序列为第二，在网络连通系数的影响中排第三，这是因为CC方法计算网络的中心性，即与计算网络效率下降比例的评估方法同样考察平均路径长度的变化，故在抗毁测度指标上表现较BC方法更好。

4 结论

笔者提出的SAW-DPDP方法通过多指标的方式对ad hoc网络中的节点进行评分排序，用删除法验证其准确性，在考虑网络中关键节点对拓扑结构影响的情况下，对评分排序进行一定的修正。综合的方法中不仅有局部拓扑信息，也加入了全局拓扑信息指标[13]。仿真结果表明：SAW-DPDP方法由于综合的元素较多，因此适用性较单一评估方法更强，且能够有效判断ad hoc网络中的关键节点。但该方法也存在算法复杂度较高的问题。在未来的研究中还应考虑对需要优先保护的节点增强其防护性，以提高网络的抗毁性[14]，或应用于不同的真实网络中。