静电场测绘实验法与计算机模拟法比较分析
王 宝 元
(吕梁学院汾阳师范分校 数学与科学系,山西 汾阳 032200)
通常情况下,电荷之间的超距作用和场的作用在电荷处于静止时并没有差别,不同的电荷分布导致电场具体性状存在很大差异.因此,对静电场线的性状分布进行科学描述,能够更加直观而又全面地展现电场图像.本文基于实验测绘法和计算机模拟法,结合稳恒电流场和静电场能够满足相同数学方程的条件,获得静电场分布情况,并对其进行测绘.
1 静电场测绘实验原理
测绘静电场场强分布情况有两种方法:实验法和计算机模拟法.如果仅采用实验测量方法进行测绘,会因实验操作过程或仪器设备不当而造成各种误差;同时,在实验过程中很难保证稳恒电流场与静电场边界条件一致,导致理想静电场分布与实测数值之间存在很大出入.采用实验测量与计算机模拟计算两种方法,基于静电场和稳恒电流场边界条件唯一性原理,分别采用两同轴圆电极和两平行直电极模型,对真空状态下带等量异号电荷的长平行输电线和长同轴电缆在任一与导线垂直平面内的电场分布情况进行模拟[1].
在模拟实验中,根据静电场电荷守恒定律与方程,可知电流场和静电场电势u均满足泊松方程,对于静电场有:
(1)
其中,ρ为电荷体密度;ε为介电常数;u为电流场和静电场电势.
对于电流场有:
Δ2u=-f.
(2)
其中,f为电流源强度分布.
在式(1)和式(2)中,当f=0且ρ=0时,在该区域内无静电荷存在.此时,结合式(1)和式(2)可得如下调和方程(也称拉普拉斯方程):
Δ2u=0.
(3)
式(3)表示稳恒电流场和静电场二者同时能够满足的数学方程式.为了使运算结果简单化,得到精确的模拟数值,本文只考虑二维场的存在,则式(3)以二维调和方程表示为:
(4)
2 静电场测绘实验模型
通常对静电场进行测绘时,采用的主要模型为两平行直电极和两同轴圆电极.在两平行直电极模型(见图1)中,A与B分别表示连接于均匀导电薄层中的两个直柱电极.当电源接通后,在导电薄层平面内会产生稳恒电流场.此时,稳恒电流场边界条件包括导电媒质层与空气接触边缘和两个导电极两部分[2].
图1中的A和B两直柱电极均为等势体,电极条件为第一类边界条件.在两种导电媒质分界面中,稳恒电流场第一类边界条件与静电场边界条件相似,其符合静电场中电位移法向量和电势连续边界条件,即满足如下条件:
J1n=J2n.
(5)
其中,j为稳恒电流密度;n为电位移法向量.
u1=u2.
(6)

图1 稳恒电流场测绘时的两平行直电极模型
结合欧姆定律可知,在第二类边界条件中,稳恒电场中电场强度和电流密度的法向量为0,即稳恒电流电场线与其边界区域平行.
图2为两同轴圆电极模型,图中圆柱导体A的轴和半径为R的圆筒导体B的轴重合.其中,圆柱导体A与圆筒导体B分别与直流稳压电源正负极相连.当圆筒导体B与圆柱导体A接触某一均匀导电媒质薄层时,此时会有径向电流在圆筒导体B与圆柱导体A柱面与筒面之间产生,从而构建起一个稳恒电流场.若电极导体和导电媒质(如导电纸)分别为导体与绝缘体时,可将电极表面作为一等势面.在此状态下,导电介质中带有静电的导体表面同样为等势面,即静电场中电极电势值属于第一类边界条件[3].

图2 静电场测绘时两同轴圆电极模型
3 静电场测绘实验与计算机模拟结果分析
在实验测绘分析时,基于有限差分法将电势所能满足的一类与二类边界条件和拉普拉斯方程均转化为相应的差分方程.在此基础上,基于数学迭代方法,对模拟实验结果进行数值计算,以此求得二维平面内静电场各点电势的数值解.最终,分别得到稳恒电场两平行直电极模型下的电势分布图(见图3)与等势线图(见图4)及两同轴圆电极模型下的静电场电势分布图(见图5)与等势线图(见图6).
在稳恒电场两平行直电极模型中,分别将半径r0=0.5 cm的A和B两电极对称置于边长为15 cm的正方形导电媒质薄层(导电纸)中心,两电极圆心相距4 cm,两电极电源电势V0=10 V,A和B两电极电势分别为5 V和-5 V.从图3和图4可以看出,在正方形导电媒质薄层(导电纸)边缘,稳恒电场两平行直电极模型下的等势线同等势边界垂直,由此证实了模拟实验中提出的假设“稳恒电流电场线与其边界区域平行”.
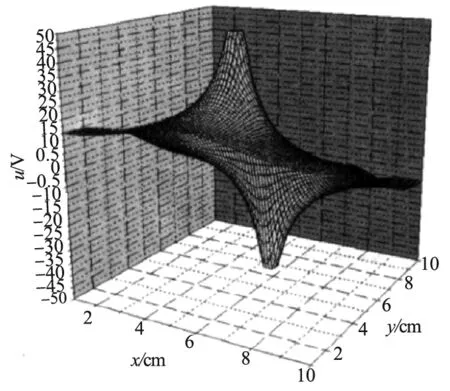
图3 稳恒电场两平行直电极模型下的电势分布图
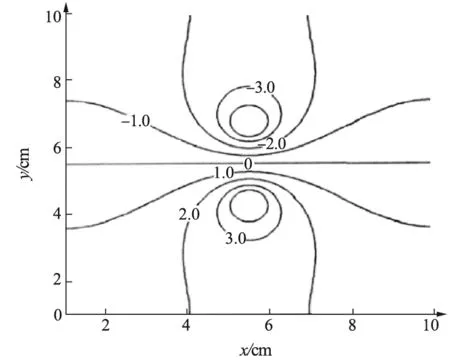
图4 稳恒电场两平行直电极模型下的等势线
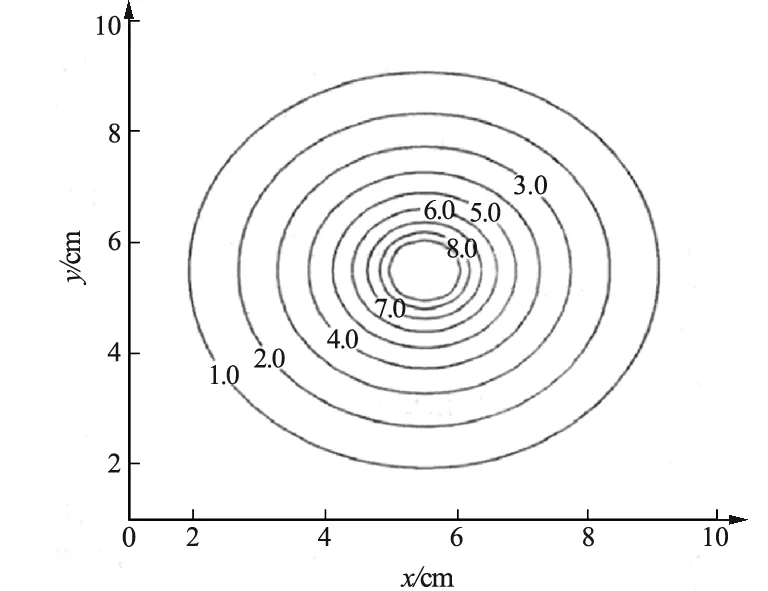
图5 静电场两同轴圆电极模型下的电势分布图
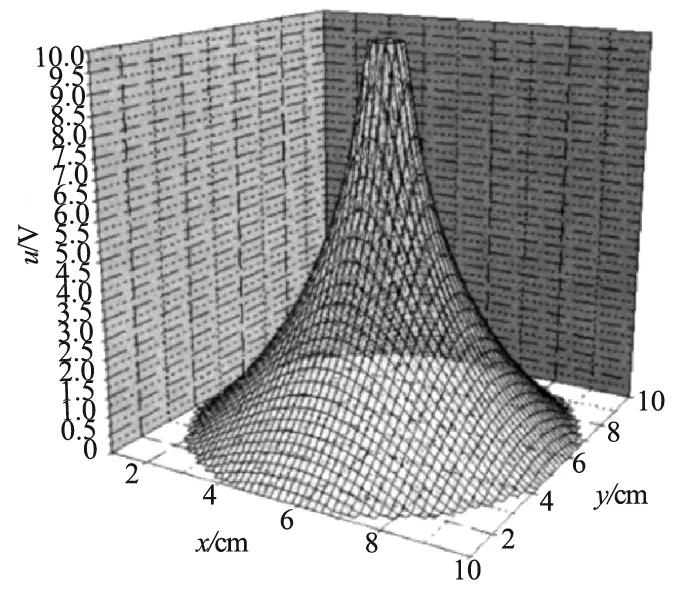
图6 静电场两同轴圆电极模型下的等势线图
在静电场两同轴圆电极模型中,采用同样的方法分别将r0=0.5 cm的A和B两电极对称置于一边长为15 cm的正方形导电媒质薄层(导电纸)中心,两电极圆心相距5 cm,两电极电源电势V0=10 V,A和B两电极电势分别为5 V和-5 V,从图5和图6中可以看出,电势在A和B两电极中心电极周边变化十分快,离A和B两电极的中心以及电极越远,电势变化速度越慢.
为了进一步凸显导电媒质薄层(导电纸)边缘的静电场效应,在计算机模拟计算过程中,可使导电媒质薄层(导电纸)足够大,从而确保A和B两电极均匀置于导电纸中心区域.在原来15 cm×15 cm的基础上,适当将导电纸放大至75 cm×75 cm,以同样的电极圆心距离、电源电势、电极电势条件,在计算机中模拟绘制稳恒电场两平行直电极模型下的等势线图和静电场两同轴圆电极模型下的等势线图,最终得到大导电纸中心部分的等势线图(见图7).
通过对比可以看出,图4与图7之间明显存在差异:远离A和B两电极边缘等势线(±3 V,±4 V)无明显变化,但远离A和B两电极边缘的等势线(±1 V,±2 V)发生了明显变化;靠近A和B两电极边缘的等势线(±3 V,±4 V)无明显变化,但靠近A和B两电极边缘的等势线(±1 V,±2 V)发生了明显变化.由此表明,距离导电媒质薄层(导电纸)边缘越远,导电媒质薄层(导电纸)的边缘效应越弱.从图7可以看出,等势线几何形状与偏心圆接近,与静电场场强分布理论相符.由此说明,采用计算机模拟计算方法得到的等势线图与理想的静电场场强分布图更为接近.

图7 稳恒电场与静电场在大导电纸中心部分的等势线图
4 结语
本研究采用实验测绘法与计算机模拟计算两种方法,详细对静电场场强分布状况进行描述.通过定性描述与定量分析,得到了不同边界条件下的静电场场强分布等势线图.研究结果表明,基于计算机模拟方法模拟静电场电势分布状态,结果较为准确、客观,能够减少因实验操作过程或仪器设备不当带来的误差,拟合结果接近理想的静电场分布状况.

