从媒质受力分析其电极化响应与磁化响应的两种等效描述

潘 锐，聂铸阳，林 方，姚 欣，王 磊，张潇潇，唐 禹，纪智宏，聂 娅，余 天，龚 敏

(四川大学 物理学院,四川 成都 610065)

通常力的概念在电磁理论中并不突出，但这并不表示力及相关现象在经典宏观电磁场理论中不重要.从历史上看，电学和磁学分别发端于人们对摩擦后琥珀吸引轻小物体与磁铁矿吸引铁制物体的直观观察[1]，安培提出“电-动力学”(Electro-dynamics)的本初含义就是研究“动电”之间相互作用力规律的科学[2]；麦克斯韦方程组是电磁场时空演化的完备规律，但真正将经典宏观电磁理论推上理论最高峰的却是以洛伦兹力公式为核心内容之一的经典电子论[3].

经典宏观电磁理论主要的研究对象是具有空间弥散特性的特殊物质——电磁场.在大学经典宏观电磁理论课程的教与学中， “场”的概念始终处于突出地位，但电磁场作用力实则仍关系着经典宏观电磁理论的基础.举例而言，经典宏观电磁场是借由其对带电体的作用力而定义的[4, 5]：惯性系中静止的带电体感受到的由另一带电体引起的作用力是为电场力，当该带电体发生相对运动时其还可能感受到与相对运动速度有关的额外作用力，这就是磁场力，即

F=FE+FB=QE+Qv×B

(1)

这也就是洛伦兹力公式，其中FE=QE是电量为Q的带电体受到的电场力，E刻画了空间此处的电场称为电场强度；FB=Qv×B是电量为Q以速度v运动的带电体所受磁场力，B刻画空间此处磁场称为磁感应强度.又例如，带电体受洛伦兹力作用，其速度大小和方向均可能改变，容易由力学动量定理与动能定理得到

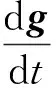
(2)

(3)

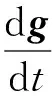
本文从媒质电磁场作用力的角度考察简单媒质两种重要宏观电磁响应——电极化与磁化——的两种等效描述，基于简单媒质受到的电场作用力在极化电荷分布和电极化强度两种电极化描述下相等以及简单媒质受到的磁场作用力在磁化电流分布与磁化强度两种磁化描述观点下相等，提供一种分析极化电荷密度与电极化强度间关系以及磁化电流分布与磁化强度间关系的新方法，证明极化电荷分布与极化强度，以及磁化电流密度与磁化强度分别是简单媒质电极化与磁化的两种等价描述.

1 媒质的电极化和磁化响应的等价描述

媒质是有限空间内以实物粒子(或称“分子”)构成的物质.在经典宏观电磁理论中，分子具有内部电磁结构且不显示量子波动性.媒质宏观电磁响应是分子在外电磁场作用下微观电荷和/或电流分布调整的宏观表现[9-11].媒质宏观电磁响应主要有电传导、电极化与磁化.简单媒质是均匀、线性且各向同性的媒质.在惯性系中相对静止的简单媒质的上述三种电磁响应能力可由标量电磁参数：电导率、电极化率和磁化率分别独立描述.我们以下着重考察简单媒质在外电场作用下的电极化响应和在外磁场作用下的磁化响应.

1.1 媒质电极化响应的两种等价描述

简单媒质即使不含大量可自由运动带电粒子也可直接对外电场做出电磁响应.一方面，非极性分子原本重合的正负电荷中心不再重合，正和负电荷中心分别沿着和背离此处电场方向发生微小移动并使媒质分子具有电偶极矩，此称为感应极化；另一方面，极性分子固有电偶极矩获得增强并转向外电场方向，称为取向极化.可见，在外电场作用下媒质的电极化响应微观上是其分子具有了沿外电场方向的分子电偶极矩pi，其宏观效果是媒质整体显现非零电偶极矩.显然地，单位体积媒质具有的电偶极矩是其电极化响应的自然量度，称为电极化强度，即

(4)

从上述媒质电极化的电偶极子描述出发，利用给定的电偶极子在外电场E0中受到的电场力普遍形式[6-8]：

(5)

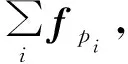
(6)

这里积分区域V是媒质所在空间.利用矢量积分恒等式

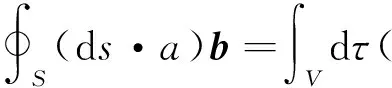
(7)

不难得到

(8)

其中面积分边界S为媒质外表面，ds=dsen，en是媒质表面处法向单位矢量.注意到简单媒质所受电场力普遍形式：

(9)

其中dq由体电荷密度ρ、面电荷密度σ或线电荷密度λ等具体电荷分布决定.式(8)表明简单媒质在外电场E0中因电极化而受到的作用力总可等效为外电场E0对媒质上述两种等效电荷分布作用的合，即

(10a)

(10b)

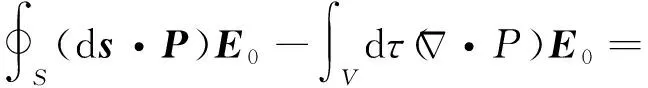
(11)

故由式(4)～(6)可知由极化电荷体密度ρP和极化电荷面密度σP共同确定的P就是简单媒质响应外电场而具有的电极化强度.

综合上述两方面，在简单媒质的电极化响应描述中，用极化电荷分布ρP和σP的描述与直接采用电极化强度P的描述是等价的.

1.2 媒质磁化响应的两种等价描述

一切媒质都能对磁场发生响应.从安培分子环流模型出发，构成简单媒质的分子具有环形电流i称为分子环流，其环绕区域的面积为a，换言之，每个媒质分子可视为一磁偶极子，其磁偶极矩按定义为

(12)

无外磁场时，微观上媒质各分子的分子环流绕行方向随机取向，其宏观统计平均为零，媒质不显现宏观磁效应；在外磁场作用下，媒质分子环流绕行方向沿外磁场取向，使得媒质显现统计平均非零的宏观磁矩，此即媒质的磁化响应.显然，给定体积媒质的宏观磁偶极矩是媒质磁化响应状态的自然量度

(13)

称为磁化强度.

与媒质电极化类似地，从上述媒质磁化的磁偶极子描述出发，利用给定的磁偶极子在外磁场B0中受到的磁场力普遍形式[6-8]

(14)

可得媒质因磁化而受到的磁场作用力为

(15)

注意到媒质区域V的体积分与媒质外表面S满足关系

∮Sds(B0·M)

(16)

而

(17)

利用矢量三重叉乘关系，(a×b)×c=b(c·a)-a(c·b)，可得

∮S(M×ds)×B0=∮S[ds(B0·M)-M(B0·ds)]=

∮Sds(B0·M)-∮SM(B0·ds)=

(18)

也即有

(19)

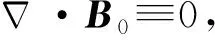
(20)

因为我们只需考虑此处媒质受彼源产生的外磁场B0作用，故有[7]

(21)

换言之，此时在媒质区域我们得到

(22)

对照于简单媒质受磁场力普遍形式

(23)

不难发现简单媒质在外磁场中磁化受到的作用力可以等效为外磁场对简单媒质因磁化而具有的两种电流分布的作用，即

(24a)

(24b)

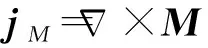
(25)

再注意到 式(13)—(15)可知体磁化电流密度jM和磁化电流面密度kM共同确定的M就是简单媒质因响应外磁场而具有的磁化强度.

可见，在简单媒质的磁化响应描述中，采用磁化电流分布jM和kM的描述与直接采用磁化强度M描述两者是等价的.

2 讨论

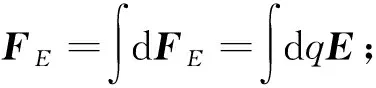
此外，现行多数教材基于媒质理想化几何模型的思路推导通常需分两步：先由媒质理想化几何模型导出电极化强度与极化电荷体密度以及磁化强度与磁化体电流密度的微分关系式，即

(26)

(27)

再考虑在边界处积分方程得到极化电荷面密度与电极化强度以及磁化电流面密度与磁化强度局域关系

σP=en·P

(28)

kM=-en×M

(29)

这里从媒质受力效果出发，我们提供了一种直接获得极化强度与极化电荷密度、磁化强度与磁化电流密度完备关系的方法，无需额外讨论媒质内部与边界区别，更加直接明了.

最后，本文提供的方法侧重于公式物理含义解析较少借助理想模型的具体分析，虽对数理基础提出较高要求, 但在教与学实践层面能更充分展现电磁理论课程“从公式中读物理”的自身特点和训练要求,对开拓学生思路也具有一定参考价值.

3 总结

电场对电荷产生力的作用，磁场对电流产生力的作用，这是电磁场的基本性质之一.本文由此出发，分别考察媒质在外电场和外磁场下的受到的电场力和磁场力，分别获得了电极化强度与极化电荷分布以及磁化强度与磁化电流分布的等效关系.该方法较少借助媒质微观结构的理想化几何模型，并在获得极化电荷体密度和磁化电流体密度的同时可以直接获得界面处的极化电荷面密度和磁化电流面密度.