关于“拍”现象的直观教学

夏峥嵘，李荣青，童 悦， 徐小雪

(淮南师范学院 物理系 安徽 淮南 232038)

两个频率相差不大、振动方向相同的简谐振动在空间叠加时，合振动的振幅随时间作周期性变化，这一现象称为“拍”现象. 如： 两个固有频率相差不大的音叉发出的声波进行叠加时，会听到“嗡嗡”的声音，就是声音产生的“拍”现象. “拍”现象被广泛应用于光学测量[1-2]、传感技术[3-4]和机械动力系统[5]等领域,理解“拍”现象的形成原因和特点有利于加深学习者对其本质的认识.近年来，对“拍”现象教学研究主要集中在 “拍”现象的实验展示[6-8]和合振动包络曲线为零处前后半振动损失讨论[9-11]两个方面.在此研究基础上，本文针对“拍”现象这一教学内容，运用旋转矢量图[12,13]的优点，直观形象地分析 “拍”现象振动规律的构建过程，解释拍现象中振幅变化特点及相位突变的形成原因.这种分析方法能直观呈现 “拍”现象的物理特点，帮助学习者深刻理解“拍”现象的本质，有效提高课堂教学效果.

1 “拍”现象的一般教学方法

现设两个振动方向相同，频率相差不大的简谐振动方程分别为

x1=A1cos (ω1t+φ10)

(1)

x2=A2cos (ω2t+φ20)

(2)

其中A1、A2分别为两个分振动的振幅，ω1、ω2为两个分振动的频率，φ10、φ20分别为两个分振动的初相.为研究问题的方便，设振幅A1=A2=A0，初位相φ10=φ20=φ0，且ω1>ω2.根据三角函数运算法则可知两个简谐振动叠加形成的合振动为

(3)

这种合振动的振幅不再是一恒定值，而随时间作周期性变化的现象，称之为“拍”现象.其振幅变化规律为：

(4)

(5)

(6)

通过三角函数的运算能从理论上简洁地获得 “拍”现象的变化规律，但是对“拍”现象的形成过程机制缺少直观形象的展示和分析，学生对“拍”现象的认知局限在抽象的理论公式层面，缺少对其变化规律及其本质的深刻理解.而旋转矢量图示法因其直观、形象的特点被广泛地应用于机械振动和机械波的教学研究中.下面我们将通过旋转矢量图示法具体直观地呈现“拍”现象的形成过程，从而加深对“拍”现象中变化规律的深刻认识.

2 “拍”现象的直观教学方法

2.1 旋转矢量图示法

如图1所示，画坐标轴OX，从原点O点作一矢量A(称为振幅矢量)，矢量的长度等于振幅A，矢量初始与Ox轴之间的夹角为简谐振动的初相φ0.然后使得振幅矢量A在平面内以等于圆频率w的角速度绕O点逆时针匀速旋转，经过t时间振幅矢量转过wt的角度，与Ox轴之间的夹角为(ωt+φ0)，此时的夹角即为简谐振动在t时刻的相位.那么振幅矢量A的端点在Ox轴上投影点的位移恰好为简谐振动的位移，即

x=Acos (ωt+φ0)

(7)

故振幅矢量A任一时刻在x轴上的投影恰好描述了一个简谐振动.

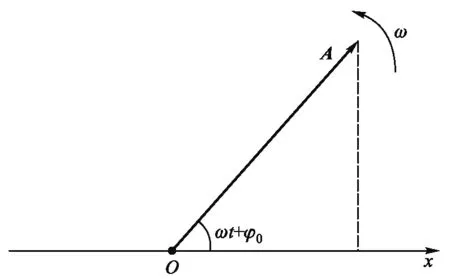
图1 简谐振动的旋转矢量图表示法

2.2 “拍”现象的旋转矢量图示法

在简谐振动的旋转矢量图示法中，式(1)、(2)中两个简谐振动的振幅矢量A1和A2分别以角速度ω1和ω2绕O点逆时针匀速转动，如图2所示.由于两个分振动的角速度不同，导致两个分振动的振幅矢量A1和A2之间的相对位置(即Δφ)随时间周期性变化，合振动的振幅矢量大小也将随时间作周期性变化，即形成“拍”现象.下面我们将以一个周期为例探讨论“拍”现象中各物理量的变化规律.

图2 “拍”现象形成的旋转矢量图

2.2.1 “拍”现象中合振幅的变化规律

初始时刻分振幅矢量之间的夹角Δφ为0，故此时合振幅A最大，为2A0；随着时间的增大，分振幅矢量之间的夹角Δφ逐渐增大，合振幅逐渐减小；直至两分振幅矢量之间的夹角Δφ为π时，合振幅A减至最小值0.同理，当分振幅矢量之间的夹角Δφ从π逐渐增大到2π时，其合振幅A又从0逐渐增大为2A0，此时振幅矢量完成了一个周期内的变化.

根据矢量合成法则，对矢量A1与A2进行矢量叠加，容易导出合振动的振幅矢量A的变化规律和式(4)相同，这里不再赘述.

2.2.2 “拍”现象的周期和频率

振幅矢量A2相对A1以ω2-ω1角速度逆时针匀速转动，其相对位置是周期性变化的，导致合振幅矢量的大小也呈周期性变化的规律，其相对位置变化的周期即为合振幅变化的周期，如图2所示.根据圆周运动的规律可知振幅矢量A2相对于A1旋转一周需要的时间，即

根据周期和频率的关系即可得到拍频率，形如式(6).

3 “拍”现象中相位突变的讨论

根据旋转矢量图知当两分振幅矢量的夹角Δφ=π时，其合振幅为0.而当Δφ=π-δ(δ→0)时，其合振动的相位在图3(a)中标注的位置，其相位为

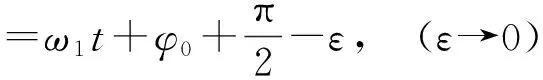
(8)

当Δφ=π+δ时，其合振动的相位在图3(b)中标注的位置，其相位为

(9)

故在合振幅A=0前后，“拍”现象中合振幅矢量的相位发生了π的相位突变，相位突变在一定条件下会给合振动振幅矢量带来半振动损失[6-8].

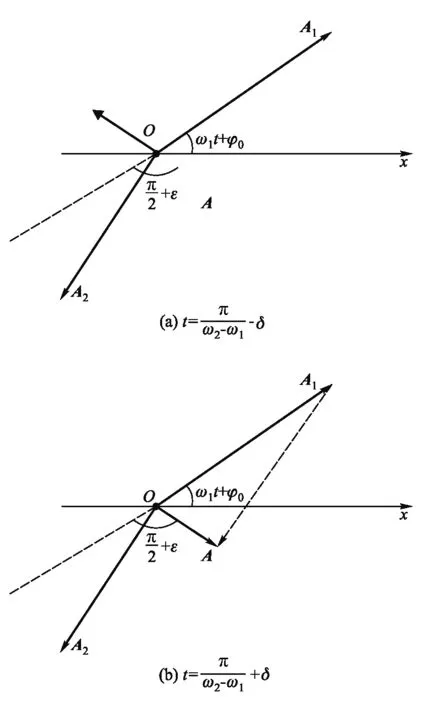
图3 “拍”现象中合振幅矢量的相位突变

当然，根据旋转矢量图示的振幅和相位变化规律，很容易获得“拍”现象的运动方程式(3)，这里不再详述.

4 结束语

本文利用旋转矢量的方法，借助几何图形直观形象地呈现了“拍”现象中振幅变化的原因和规律，同时利用旋转矢量图清晰地展示了“拍”现象的周期、频率及形成过程中相位变化的特点及相位突变的原因.这种方法在一定程度上有助于学生形成“拍”模型的清晰表象，让学习者不仅掌握“拍”现象的变化规律，更能理解形成这些规律的本质原因，从而加深对“拍”现象相关知识的理解和认识，留下深刻永久的知识图像.