矩形与圆形截面载流平行双导体间安培力研究

张盛源，徐天福，郭芳侠

(陕西师范大学 物理学与信息技术学院，陕西 西安 710119)

在工程上，狭小的配电箱内电力系统的母线为矩形截面以减小母线间的安培力.那么矩形截面载流导体间的安培力与截面尺寸有何关系？截面尺寸一定时，与放置方向有无关系？与同面积同电流的圆截面导线的安培力有多大的差异？要回答此些问题，就要从导体周围的磁场的分布开始研究.关于截面形状不同的无限长载流导体磁场研究，文献[1-3]讨论了无限长载流圆柱面和圆柱体产生的磁场，文献[4]讨论了无限长截面为矩形和三角形的载流导体产生的磁场，但都缺乏磁感线分布的直观图像以及对不同截面平行载流双导体间安培力的分析.文献[5]虽有讨论截面为矩形的载流导体间的作用力，但把导体产生的磁场看成若干个无限大平面产生的磁场叠加，该模型不够精确.本文根据毕奥-萨伐尔定律及安培环路定理，分别计算无限长截面分别为矩形和圆形的载流直导体产生的磁场，并利用Matlab模拟了磁场分布；随后计算两个矩形截面的载流导体间安培力和两个圆形截面的载流导体间的安培力，并进行对比分析.

1 矩形截面与圆形截面载流导体产生的磁场的计算与模拟

对于铜导线，室温下σ=5.9×107S·m-1，μ≈μ0=4π×107N·A-2.因而f=50 Hz时，δ≈9.4 mm；f=1000 Hz，δ≈2.1 mm，低频下趋肤深度与电力系统导线线径同数量级；从电流密度看，即便是1000 Hz的交流电，以圆柱导体为例，导线轴线和表面处的电流差别也不会很大.因而在低频情况下趋肤深度效应可以忽略，近似认为电流在横截面上均匀分布[7].

1.1 无限长的矩形截面载流导体周围磁场

任意导线元M在P点的磁场dB及其分量如图1所示.根据无限长直导线的磁场公式[6]：

导线元在P点产生的磁场大小为

该磁场的x分量为：dBx=dBcosθ，其中

代入得

同理得y分量为

图1 无限长矩形截面导体周围磁场分析

由此可得整个载流导体的磁场分量可表示为

(1)

(2)

积分运算得到无限长的矩形截面载流导体在(x,y)处的磁场分量的表达式：

(3)

(4)

根据磁感线的定义，磁感线上每一点的切线就是该点磁感应强度的方向，故在磁感线上取一段线元dl，它应与B平行，故：dl×B=0.

由上式可得xy平面内磁场线微分方程：

(5)

将式(3)、(4)代入上式，积分便可求得磁场线方程.在这里利用Matlab求得近似的数值解并绘制磁感应线.图2(a)、(b)、(c)是假设b=1 cm，a分别取0.25 cm、0.5 cm、1 cm的磁感线分布.

根据图像分析可得，矩形截面导体长和宽的差异越小，导体形成的磁场线越接近于圆[图2(c)]；长和宽的差异越大，磁场线越来越扁[图2(a)]，类似于椭圆；若某一边的长度为无穷大，即导体变成有一定厚度的面积无限大的平面导体，其磁场线为平行于导体面的多条直线，这和电磁学的一般规律相符合.

图2 无限长矩形截面导体周围磁感线分布

1.2 无限长的圆形截面载流导体周围磁场

根据以上所述磁场的特点，由安培环路定理∮B·dl=μ0∑I[6]易知磁场表达式为

(6)

2 矩形截面与圆形截面载流双导体间的作用力及分析

2.1 矩形截面无限长载流双导体间的作用力

为研究方便，在图1磁场中置入电流为I′的无限长同规格电流同方向的矩形直导体如图3所示.考虑导体长度为l的一段所受的磁场的作用力，设原点处的导体产生的磁场作用在l上的安培力为Fr.设|OQ|=L,将导体段分为无穷多平行的无限长直导线元，其电流可表示为dI′=j′dxdy.再对导线元应用安培力公式：

dF=Idl×B

(7)

图3 矩形截面载流双导体间的作用力

根据几何关系将力分解为dFy=j′lBxdxdy和dFx=-j′lBydxdy，由对称性分析可知

(8)

因此长为l的一段所受的安培力沿x轴负方向，大小为

Fr=|Fx|=∬j′lBydxdy

将式(4)代入上式，并积分得

(9)

为了更直观地了解当矩形导体边长之比不同时，两导体间安培力随距离L的变化情况，设I=I′=1A、l=1 cm，导体截面积为1 cm2，分别取a=0.5 cm、0.8 cm、1 cm、1.2 cm、1.5 cm，计算相应的b，作Fr-L图线如图4所示.

图4 矩形截面载流双导体间作用力Fr随距离L的变化

由图4可以看出，在电流密度和尺寸一定的条件下：横截面的边长比a/b一定时，安培力随着距离L的增大而减小；距离L一定时，a/b的值越大，安培力越小，所以配电箱内两矩形截面母线放置时应使较长的边相对，这样安培力小于同距离短边相对时的安培力.

2.2 圆形截面无限长载流双导体间的作用力

两无限长同规格圆柱载流导体的位置，如图5所示，设轴线间垂直距离为L，电流密度分别为j和j′.考虑长度为l的一段所受的作用力，设该段载流导体所受的安培力为Fc，建立柱坐标系.

图5 两圆形截面载流导体间的作用力

把载流导体看做许多无限长的平行直线导线元组成，P(r,θ)处的导线元所受的安培力大小为dF=j′lBrdrdθ.由圆截面导体对称性可知两导体间总的安培力在垂直于极轴方向的合力F⊥=0，总的安培力方向平行于极轴，即

代入并积分可得

(10)

2.3 矩形与圆形截面双导体间安培力的比较

令两安培力表达式(9)、(10)中的j、j′、l分别对应相等，作比值Fr/Fc

(11)

假设矩形与圆形导线横截面积ab=πR2=1 cm2，作出Fr/Fc-L如下图7所示.

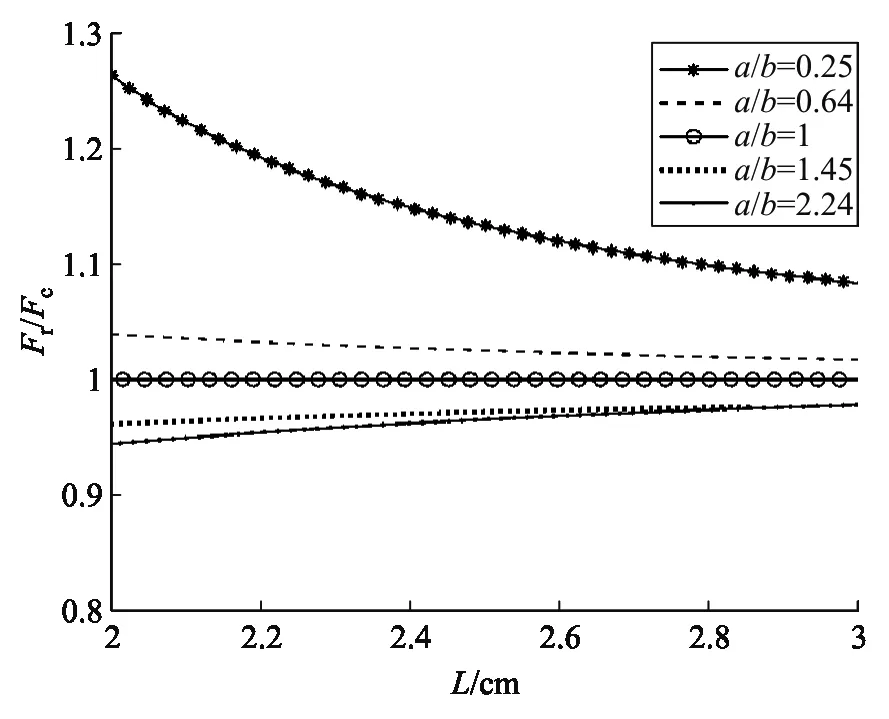
图7 Fr/Fc-L图

该图像表明两种导线电流密度和尺寸对应相同时，当距离L越来越大，Fr/Fc趋近于1；若L一定，Fr/Fc随着a/b的值变化：a/b<1时，Fr/Fc>1，此时矩形截面导体间作用力大于圆形截面间作用力；a/b=1时，Fr/Fc≈1，此时矩形截面导体间作用力近似等于圆形截面间作用力；a/b>1时，Fr/Fc<1，此时矩形截面导体间作用力小于圆形截面间作用力.总体来看，a/b越大，Fr/Fc比值越小.这就是为什么配电箱选用矩形截面导线进行电流配送，而且放置时应保证相对的边长度大于另一边长度.

3 结论

通过以上的理论计算得到了无限长矩形、圆形截面通电导体周围的磁场分布和平行双导体间作用力的表达式，并在Matlab的辅助下进行了模拟分析.得到如下重要结论：1) 矩形截面载流导体磁感线近似椭圆状，在边长相等时近似为圆形；2) 电流密度和尺寸一定时，两个矩形截面平行载流导体间的安培力与距离、边长比相关，边长比a/b越大，作用力越小；3) 在电流密度和尺寸相同时，与两个圆截面间的作用力比较：当a/b>1时，矩形截面间的作用力较圆形的小；a/b<1时，矩形截面间的作用力较圆形的大.根据这个规律，狭小的配电箱应选用矩形截面导线，且放置时应保证相对的边长较另一边大,才能保证安全.