用变分优化正交的连带Laguerre基函数计算无支撑单层MoS2中激子的能量和波函数

吴曙东, 王 强, 程立文

(扬州大学 物理科学与技术学院, 江苏 扬州 225002)

近年来，具有二维层状晶体结构特征的过渡金属硫族化合物(化学式为MX2，其中M=Mo、W 等; X = S、Se或Te)因其独特的电学和光学性质而激起了人们的极大研究兴趣，在光电领域中具有广阔的应用前景[1-7]. 以单层MoS2为代表的过渡金属硫族化合物是一种新型的类石墨烯二维层状材料，在位于布里渊区K和K′点的导带和价带之间有1.9 eV的直接带隙，这对光电应用至关重要[7]. 此外，单层MoS2的谷圆偏振光独特的选择吸收允许有效地控制其自旋和谷自由度[8]. 激子是电子和空穴在静电库仑力作用下相互吸引的束缚态. 以前的理论和实验结果表明，激子效应在决定单层MoS2的光学性质方面起着重要作用. 在室温下可以观测到不同于块体材料高达几百毫电子伏的激子束缚能，并且可以观测到更高阶的激子态。除了极大的激子束缚能之外，还有强激子吸收. 例如，在单层MoS2中观察到非常强的直接跃迁光致发光. 与块体材料相比，其发光量子效率显著提高了104倍以上[7]. 研究结果还表明，在单层二维材料中，激子的静态介电函数不再是定值，而是随着主量子数的变化而变化，其来源于介质的介电屏蔽效应[3,9,10]，因此其能量本征值问题没有解析解.在准确对角化方法中，选择合适的基函数是很重要的.连带Laguerre基矢是高度局域化和灵活的基函数，并且已经被证明是高精度计算的一个很好的选择，因为它们是正交的，并且比类氢轨道和高斯型轨道收敛更快[11]. 在变分优化下，连带Laguerre基矢仅几个简单的轨道就可以收敛，具有丰富的物理意义，然而其它的基矢是基于大量的基函数，使描述复杂化. 本文将以无支撑单层MoS2为例，采用了一种基于变分优化的正交归一化的连带Laguerre基矢的准确对角化方法计算了单层MoS2中A型激子的能量和波函数，其中哈密顿量的矩阵元中不涉及显式积分. 通过对收敛性的检验和文献数据的比较来评估该方法的收敛效率和有效性.

1 理论模型与计算方法

激子是一个因库仑吸引力束缚在一起的电子-空穴对.在有效质量近似下，在单层MoS2中激子的哈密顿量可写为

(1)

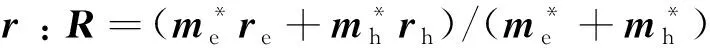
(2)

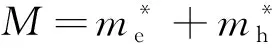
(3)

除非特别说明，本文中使用Rydberg(里德堡)原子单位(e2=2，ħ=1，μ=1/2)。在单层MoS2材料中，激子是在一个二维平面内运动.在极坐标(r,φ)中，电子-空穴对相对运动的薛定谔方程为

(4)

其中E和ψ(r)分别为激子的本征能量和对应的本征函数.在二维激子系统中，使用由Rytova-Keldysh导出的屏蔽库仑势[12]：

(5)

其中H0和Y0分别为零阶Struve函数和第二类Bessel函数，r0为单层MoS2的激子介电屏蔽长度.

对于屏蔽库仑势，其本征值问题没有解析解. 因此，采用变分优化的准确对角化方法求解方程(4)，将激子波函数展开为一组二维正交归一化的连带Laguerre基函数[11]

(6)

其中

(7a)

和

(7b)

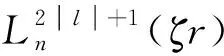
将式(6)代入式(4)，得到关于Cnl的本征值方程

(8)

其激子哈密顿量矩阵元有如下的形式

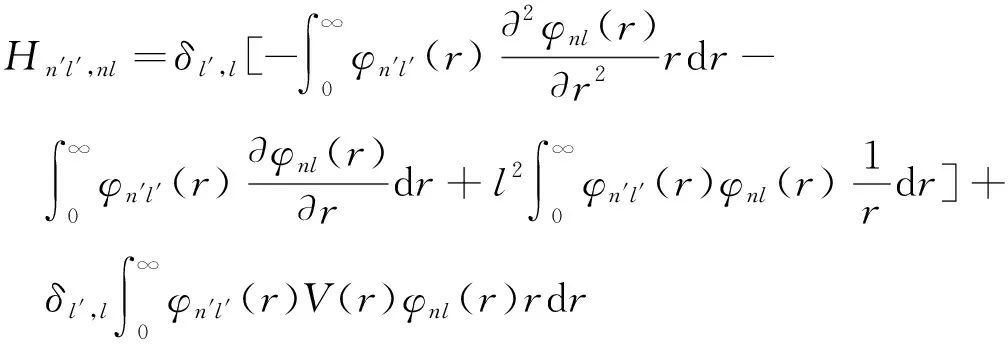
(9)

其中δn′,n和δl′,l是Kronecker delta函数. 从式(9)可以看出n不再是好量子数, 但l仍然是好量子数，因此激子本征态可根据l来分类.

为了使Hn′l′,nl中不涉及显式积分，我们推导了激子哈密顿量矩阵元的解析形式. 连带Laguerre多项式由以下公式显式给出[11]

(10)

(11)

在式(9)中基于连带Laguerre基函数积分是可积的. 对于l′=0和l=0的情况,Hn′l′,nl可写为

(12)

对于l′≠0 或l≠0的情况,Hn′l′,nl可写为

(13)

激子哈密顿量矩阵元的解析表达式大大简化了计算，因为大部分计算时间都花费在激子哈密顿量矩阵对角化上，而不是矩阵元素的计算上.激子哈密顿量矩阵是实的，对称的，稀疏的.在计算了激子哈密顿量矩阵后，采用变分优化的对角化方法得到激子本征能量和其对应的本征函数.在选定基函数大小的情况下， 用里兹变分原理通过改变ζ的值使能量最小化.因此，其步骤如下:

1) 初始化各能级Enl的变分参数ζ的值；

2) 将本征值方程(8)对角化得到能级Enl和波函数ψnl(r,φ)；

3) 调整参数ζ的值并跳到步骤(2)，直到找到了能量最小值Enl, 此时即为基态和激发态的能级Enl和波函数ψnl(r,φ).

2 计算结果与讨论

(14)

图1所示为变分参数ζ和相对误差ε(N)随基矢大小N的变化情况.如图1(a)所示，当N从3连续变化到20,ζ值显示出随着N增加而显著增加的阶梯状行为. 这是因为随着N值的增大, 展开的基函数的数量增加. 随着ζ值的增大, 基函数被径向压缩. 通过变分压缩径向波函数而移动节点位置以获得所需要的波函数. 如图1(b)所示, 相对误差ε随N增大呈指数递减的阶梯状行为, 这意味着相对于N的收敛速度非常快，表明了该方法的可靠性. 激子本征能量即使在少数基函数下也表现出非常好的收敛性. 例如，一个基矢大小为N=5的所有能量的相对误差均低于10-5, 这是因为连带Laguerre基函数在空间中非常集中，导致了相当快的收敛速度. 此外，还可以通过选择一个最合适的ζ值对收敛性进行变分优化. 综上所述可得出如下的结论：在基矢的大小足够大的情况下，可获得极好的结果. 因此，我们提出的变分优化二维正交归一化的连带Laguerre基矢是一个很好的选择.

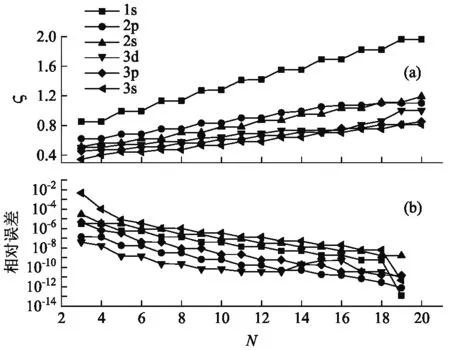
图1 (a)变分参数ζ和(b)激子本征能量的相对误差ε(N)随基矢大小N变化关系

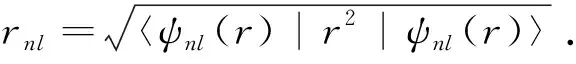
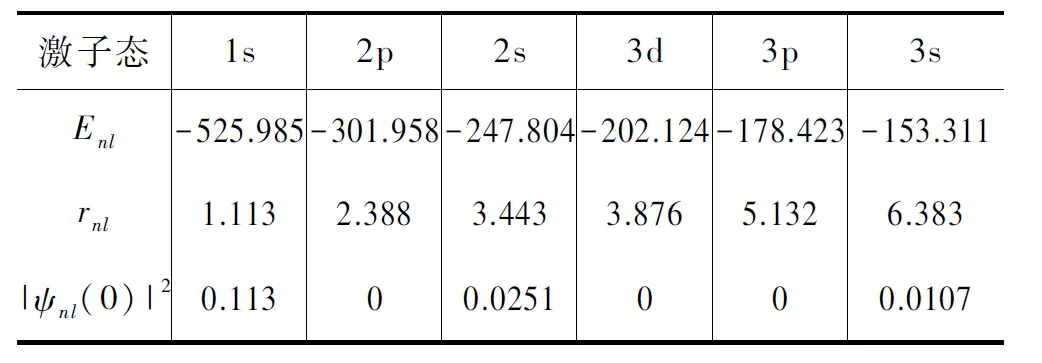
表1 在单层MoS2中，激子的6个低本征能量Enl (meV)、半径rnl (nm)和模的平方|ψnl(0)|2

图2 在单层MoS2中激子归一化的径向波函数ψnl(r)

图2描绘了A型激子的6个低本征能量的归一化径向波函数. 由于V(r)圆对称性, 我们可以把激子波函数分解成径向波函数和角度波函数. 径向波函数依赖于n和l. 在开区间的(0,∞)的节点数为n-|l|-1. 每次随着量子数n增加, 一个额外的节点产生. 每次随着量子数|l|增加, 一个额外的节点又一次消失，被通过原点的节点所代替. 1s轨道在原点有一个凸起，而它在较大距离处呈指数衰减. 它的最大值在r=0, 即为发现电子和空穴在同一空间位置的概率密度最高的点. 由于离心力项的作用，2p或3d轨道被推离原点更远, 即ħ2l2/2μr2是一种排斥力。2s或3p轨道包含一个正振幅和一个负振幅. 3s轨道在3个凸凹下变得更加分散. 这是因为随着n的增加，波函数从原点延伸得更远，包含更多的节点.

3 结论

本文基于变分优化的二维正交归一化的连带Laguerre基矢，用准确对角化方法计算了无支撑单层MoS2中A型激子的本征能量和本征函数. 介电屏蔽效应破坏了SO(3)对称性，导致了激子本征能量以反常轨道角动量的顺序出现. 在变分参数优化下，分析了当基函数的大小从3连续增加到20时，激子本征能量的收敛性. 收敛速度不仅与基函数的数量有关，而且与变分参数有关. 在变分优化的情况下，收敛速度非常快，证明了该方法的可靠性. 该方法用连带Laguerre多项式自动构造了既满足束缚态又满足连续态的正交基函数集，且哈密顿量的矩阵元不涉及显式积分. 利用正交归一化的连带Laguerre函数作为基函数，可以显著减小基矢的大小. 激子本征能量即使在少量基函数情况下也与以前的计算结果非常吻合. 因此，我们提出的变分优化的二维正交化归一化的连带Laguerre基函数是描述二维材料中激子和原子物理的一个很好选择.