“数”“形”结合在高中数学几何解题中的应用策略

（山东省泰安一中新校 山东泰安 271000）

高中数学是一门非常重要的学科，对帮助我们形成数学思维，提升数学创新意识具有非常重要的意义，作为学生我们必须加强对个人知识信息的储备，以便形成具有较高价值的新设想和新发现。几何题是数学课程中非常重要的知识点，对我们今后的数学学习有着非常大的影响，尤其是在知识结构体系构建中发挥着承上启下的关键作用，因此，掌握几何解题技巧是学习的关键[1]。由于几何题本身较为抽象，一直以来都是我们学习的难点，但将抽象的几何问题转化为相应的几何图形求解就会使得复杂问题简单化，抽象问题具体化，把抽象的数学语言和直观的图形结合起来，就是“数”“形”结合法。“数”、“形”结合解题法是几何解题的一种重要方法，其能够以较为简单、直观的方式实现对几何题的转换，更好的帮助我们掌握几何知识点，把握解题要点。

一、解题思路

在数学几何题解析过程中，关键是要明确问题与条件之间的位置、数量关系，将“数”与“形”相互对应起来，即可迅速把握解题的关键点。在熟练掌握数形结合解题方法之后，就能够更好的实现举一反三，从而更好的应对几何题。而在对“数”、“形”结合解题法运用时，应当把握其具体的解题思路，分别为：（1）三角函数、复数等均基于几何元素和条件的基础上来进行背景的构建；（2）题目所给出的代数方程式或者等式的结构中具有所包含的较为明确的几何意义；（3）图象与函数所对应的关系；（4）曲线与方程之间对应的关系；（5）数轴上的点与实数之间所对应的关系[2]。

二、几何题型解题中“数”“形”结合的应用策略

1.“数”“形”结合在几何不等式问题解题中的应用

例题1：解不等式：√（16-x2）+√（8x-x2）>4。

解析：通过将上述不等式进行变形处理，即可获得√（16-x2）>4-√（8x-x2）这样一个公式，而该公式与上述不等式是等价的。

另设：y1=√（16-x2），设y2=4-√（8x-x2），对上述等式进行变形，即可获得如下曲线方程：x2+y12=16（4≧y1≧0）以及（x-4）2-（y2-4）2=16（y2≦4）；

通过对上述两个曲线方程进行绘图观察，其均属于半圆，通过直角坐标即可表示出来：

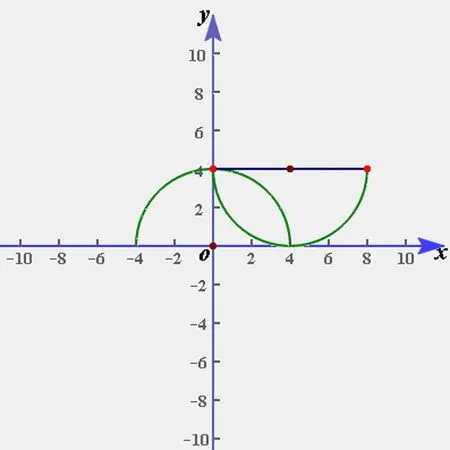
图1

例题1

根据图1来看，两个半圆之间相互交集的部位，就是本题的不等式解集，即可获得结果，{x｜0＜x＜4}。

几何不等式是较常见的几何题型，也是高考中的常考题型。对于几何不等式，在解题过程中，首先是将其化解为某个曲线方程，再根据该曲线方程来进行图形绘制，将其在数轴上表示出来，需要引起注意的是，在进行计算过程中，必须明确定义域和值域，再通过几个图像的交集情况即可获得不等式的解集。

2.“数”“形”结合在几何圆类问题中的应用

例题2：已知直线kx-y-2=0与曲线 √〔1-（y-1）2〕=x-1有两个不同的交点，求实数k的取值范围。

解析：根据直线kx-y-2=0可化成y=kx-2，可知它是经过点（0，-2），斜率变化的直线。

通过对曲线√〔1-（y-1）2〕=x-1进行变形处理，可得（x-1）2+（y-1）2=1（x≥1）（0≤y≤2），此时可知该曲线是以（1，1）作为圆心，以1作为半径的位于直线x=1右侧部分的半圆。

设直线绕过点（0，-2），并通过顺时针旋转至与圆下方相切时的斜率为k1；直线过点（0，-2）和（1，0）与圆有两个交点时的斜率为k2。可得当直线kx-y-2=0与曲线有两个不同的交点时，斜率k满足k1＜k≤k2。

由圆心（1，1）到直线kx-y-2=0的距离d=|k-1-2|/√（1+k2）=1，解得k1=4/3，

通过点斜式方法可解得k2=（-2-0）/（0-1）=2，由此可得4/3＜k≤2。

图2

例题2

通过上述例题来看，在对几何圆类问题解题过程中，通过“数”、“形”结合解题法的合理运用，能够促使解题思路更加明确，题型得以简化。对圆类问题的解答，其解题的关键是密切围绕圆与直线的位置关系、圆与圆之间的位置关系、圆的标准方程等各项问题来实现。例如：在对直线和圆的位置关系进行判断的过程中，对直角坐标系进行建立，便能够更为直观的了解到在圆外直线的表现，通过对圆心到直线的距离进行计算，若距离大于圆的半径，即表示直线处于圆外，这种方法是“数”、“形”结合解题法解答圆类问题最基本的、最常用的方法。

结语

总而言之，几何题型是高考必考内容，并且在所有题型中占据了较高的比例，尽管几何题型的难度相较于函数题型比例较低，但仍然是高中数学解题的难题，这主要是由于其本身较为抽象所导致的，但把握一定的技巧，即可快速熟练的实现几何题型的解答。“数”、“形”结合解题法的运用，能够促使题目给定的条件得以呈现和对应，使得解题时间得以缩短，且不容易出现漏题的情况，可更好的实现对答题效率和答题准确率的提升。