基于连接点的机载双天线InSAR系统相位偏置估计算法

李银伟，夏慧婷，卢护林，王海涛

(上海无线电设备研究所，上海 201109)

0 引言

InSAR是一种重要的遥感技术，能获取高分辨率的二维图像及高精度的地面高程信息。InSAR可将绝对相位信息转换为高度数据[1-4]，目前已成功应用于全球数字高程模型(DEM)的反演。在InSAR信号处理过程中，首先对配准后的两幅单视复图像进行共轭相乘得到缠绕相位，然后利用相位解缠算法[5-6]消除2π整数倍的相位模糊来获取解缠后的相位，解缠后的相位仍不是绝对相位，不能直接用于反演DEM。因此，在相位解缠后，需要估计解缠后相位和绝对相位间的差异，即相位偏置。在忽略系统误差的情况下，相位偏置是一个恒定值[7]。

传统的相位偏置估计方法通常利用场景中的自然或人造地面控制点(GCP)来估计相位偏置。利用GCP的三维坐标，可获得精确的相位偏置估计值，这使重建高精度DEM成为可能。然而，在茂密森林或沙漠的一些地区，不易获得合适的天然GCP，且难以布置人造GCP。基于频谱分集[8]和最大似然估计[9]可用于没有GCP场景下的相位偏置估计，但精度不高且耗时较多。

本文研究分析了基于连接点的相位偏置估计方法。连接点是指相邻SAR影像中具有同一地理位置特征的点，也可称为同名点。在两次干涉测高过程中，连接点的高程值可认为不变。首先，基于连接点高度不变的特征建立双天线InSAR两次采集数据中相位偏置间的线性关系；然后相位偏置的估计问题可转化为求解由众多连接点建立的超定线性方程组问题；最后通过处理X波段机载双天线InSAR实际数据可知，与传统的基于GCP的相位偏置估计算法相比，新提出的基于连接点的相位偏置估计方法具有相似的性能。

1 InSAR高程反演

机载双天线InSAR系统的几何模型如图1所示。图中：H为主天线A1相位中心的高度；h为点目标P的高度；r0为主天线A1和点P间的斜距；B和α分别为基线长度和基线倾角；θ为下视角。

图1 InSAR系统几何模型Fig.1 Geometric model of InSAR system

以天线A1为参考，得到以下表达式：

φabs=φunw+φoff

(1)

(2)

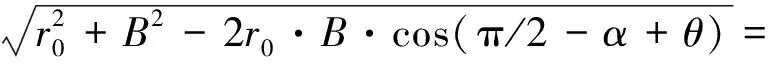
(3)

h=H-r0cosθ

(4)

式中：φunw为解缠后相位；φoff为相位偏置；φabs为绝对相位；m为与系统运行模式相关的常数变量，如果是标准模式，则m=0.5，如果是乒乓模式，则m=1.0。

根据式(1)～(3)，式(4)可表达为

(5)

2 算法

算法的数据采集模型如图2所示。对感兴趣的公共区域，可用InSAR在飞行方向的同向、反向甚至跨越飞行方向上分别获取InSAR回波数据。基于式(5)，针对2次数据采集进行成像和干涉处理获得未缠绕干涉相位后，图2中重叠区域中的点P高度可分别表示为

图2 算法的数据采集模型Fig.2 Data acquisition mode of proposed method

(6)

假设

(7)

将式(6)重写成

(8)

(9)

若点P(x,y,z)的真实高度已知，则相位偏置φoff1和φoff2可通过式(5)计算。但点P的真实高度未知，需要通过上述线性函数来估计2次采集的相位偏置φoff1和φoff2。

考虑重叠区域中如点P一样的N个连接点，可利用2个相位偏置间的关系获得N个如式(9)的线性方程组。那么，估计相位偏置的问题便转化为求解N个如式(9)的方程组解的问题。使用矢量符号重写式(9)，有

LΦ=B

(10)

(11)

(12)

(13)

在大多数情况下，该方程组是超定的，因为重叠区域中很可能存在2个以上的连接点。在方程组超定的情况下，可以获得最小二乘解，有

Φ=(LTL)-1LTB

(14)

式(14)不能区分高相干连接点和低相干连接点间的差异。为实现此目的，引入加权最小二乘解，有

Φ=(LTWL)-1LTWB

(15)

式中：W为N×N权重矩阵，在噪声不相关的情况下，其形式[10]为

(16)

式中：σN为在连接点N处干涉相位误差的标准差。可从干涉相干性中得到合理的σN值[11]，有

(17)

|γ|=|γ1|·|γ2|

(18)

3 试验结果

为了验证算法的有效性，对X波段机载双天线InSAR系统获取的实际回波数据进行处理。该系统由中国科学院电子学研究所所研发，工作在乒乓模式下。在回波数据聚焦成像中，采用具有自动配准功能的扩展波数域成像算法进行处理[12]，载机平台的运动误差采用基于IMU/DGPS测量数据的运动补偿方法进行补偿。

试验区位于四川省绵阳市郊区，地形为起伏的山地。在具有重叠区域的2个测试区域内分别布置了8个和6个GCP。通过传统的基于GCP的相位偏置估计算法可得到2次干涉测高的精确相位偏置估计值，进而获得绝对相位及测试区域的DEM，并将DEM当做测试区域的真实高程。为了评估所提算法的性能，考虑0.8的相干阈值，在重叠区域中随机分布的135个点满足阈值，用于建立线性方程组，并用所提算法估计相位偏置值。2个测试区域的SAR图像及估计的相位偏置值反演的DEM如图3所示。

图3 X波段数据处理结果Fig.3 Processing results of X-band data

为定量评估DEM反演的精度，借用均方误差(eAME)和均方根误差(eRMSE)的定义式

eAME=

(19)

eRMSE=

(20)

2块测试区域的统计结果见表1。可知， 2块测试区域的DEM误差都非常小。结果表明：本文所提算法与传统的基于GCP的相位偏置估计算法具有相似的性能，都能准确估计相位偏置。

表1 两种相位偏置估计算法的DEM误差Tab.1 DEM difference between two phase offset estimation methods

4 结束语

本文提出了一种基于连接点的相位偏置估计新算法。由于连接点高度唯一，因此相位偏置的估计问题可转化为利用重叠区域中的连接点来求解线性方程组的问题。对实际机载双天线InSAR数据处理的结果表明：使用本文所提算法估计相位偏置生成的DEM与通过传统的基于GCP的相位偏置估计算法生成的DEM具有非常相似的精度。由于不需要GCP，本文所提算法具有更低的成本和更高的效率，且能自动估计相位偏置。