一种适合于斜视TOPS SAR的改进PFA成像方法

吴玉峰，张红波，叶少华

(中国航空工业集团公司雷华电子技术研究所，江苏 无锡 214063)

0 引言

作为扫描式合成孔径雷达(ScanSAR)的改进工作模式，循序扫描地形观测(TOPS)模式通过天线波束沿方位向的主动扫描有效克服了ScanSAR模式下成像结果的扇贝效应，解决了方位模糊比和输出信噪比不一致的问题，同时保持了ScanSAR的宽测绘带能力[1]。2007年，德国TerraSAR-X卫星首次进行了星载TOPS SAR模式实验，并成功获得了聚焦良好的成像结果[2]。欧洲新一代SAR卫星Sentinel-1也利用TOPS SAR模式来代替传统的ScanSAR模式，用于宽测绘带及超宽测绘带成像[3-4]。

由于天线波束存在沿方位向的转动，TOPS SAR回波信号的方位多普勒频谱通常会超过系统的脉冲重复频率(PRF)，即回波信号在方位频域是模糊的。根据对模糊频谱处理的不同方式，TOPS SAR的成像方法可分为子孔径成像算法[5-6]、全孔径成像算法[7-8]两类。其中：子孔径成像算法中的方位信号被分为多个子孔径，保证每个子孔径信号的带宽都小于系统的脉冲重复频率(PRF)，并进行距离徙动校正(RCMC)和距离压缩，然而子孔径算法不可避免会存在孔径划分、拼接、重叠部分的选择等问题，增加了信号处理的复杂性。全孔径成像算法采用two-step方法[9]，先进行方位向预处理获得无模糊的信号频谱，再采用传统SAR成像方法进行RCMC和距离压缩。与子孔径成像算法相比，该算法无需进行孔径划分、拼接等操作，成像效率较高，已成为行业研究热点。

极坐标格式算法(PFA)[10-11]是一种典型的全孔径成像算法。该算法处理过程简单，二维插值可采用Chirp-Z变换实现[11]，运算效率高，被广泛应用于聚束SAR的数据处理中。文献[12]对传统PFA算法进行改进，提出了一种广义PFA算法，其兼具了传统PFA算法的高效性和two-step方法对避免方位模糊的有效性，仅需要PRF略大于方位瞬时带宽，以及少量的补零操作，就能实现对滑动聚束SAR和TOPS SAR数据的聚焦。然而，该算法针对的是正侧视模式，当TOPS SAR工作于斜视时，回波信号距离向与方位向的耦合将变得异常严重，且方位扫描会带来多普勒调频斜率的方位空变问题，导致文献[12]中的算法无法使用。对于斜视聚束下的PFA算法，一般采用坐标旋转，这会导致方位采样的非均匀性[10]，使方位插值变复杂。

针对上述问题，本文对广义PFA算法进行了改进，提出了一种适用于斜视TOPS SAR数据处理的PFA成像方法。该方法采用先线性走动校正，后PFA插值的步骤。线性走动校正可以大幅降低距离向与方位向的耦合性，简化RCMC，并且走动校正后，方位向采样依然均匀，因此方位向插值可采用Chirp-Z变换快速实现。针对波束扫描、走动校正引起的多普勒调频斜率的方位空变问题，利用TOPS SAR方位聚焦时的变标过程，采用方位非线性变标(ANCS)方法[13]进行统一校正，极大提高了方位向的聚焦深度，使其适用于大场景成像。

1 信号模型

二维平面内斜视TOPS SAR工作几何示意如图1所示。图中，雷达平台以速度v沿X轴匀速直线飞行，天线相位中心到场景中心的距离为Rs。数据录取过程中，雷达平台从点M运动到点N，天线波束近似绕旋转中心Orot以角速度ω匀速转动，旋转半径长度为Rrot。波束指向从θs变化到θe，中心斜视角为θ0。

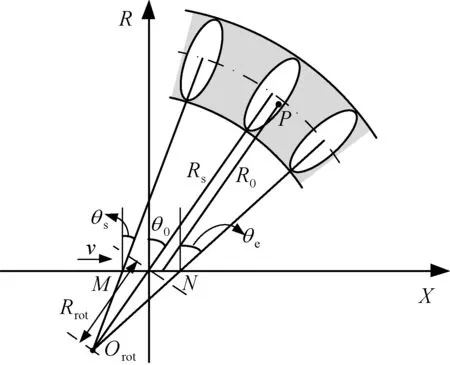
图1 斜视TOPS SAR工作几何示意Fig.1 Geometry of squinted TOPS SAR

假设雷达发射信号为线性调频(LFM)信号，则对于场景中某一点目标P(Xn,RB)，其距离脉压后的回波信号在距离波数域可表示为

exp(-jKrR(ta))

(1)

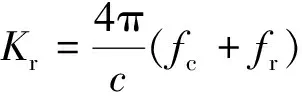
R0-sinθ0(vta-Xn)+

(2)

式中：R0=RB/cosθ0,RB为点目标P到雷达航线的最近距离。由式(2)可知，距离单元徙动包括线性走动项(ta的一次项)、距离弯曲项(ta的二次项)、高次项。由于存在线性走动项，距离向与方位向的耦合变得非常明显，这无疑增加了距离单元徙动校正的难度。此外，由式(2)可知，方位多普勒调频率为

(3)

在TOPS SAR数据采集过程中，由于天线波束转动，不同方位点具有不同的中心斜视角，因此多普勒调频率沿方位向是变化的。对于正侧视模式，cos2θ0变化较小，ka的空变性可忽略；对于斜视模式，cos2θ0变化较大，ka的空变性无法忽略，否则将导致场景边沿点严重散焦。

针对上述难题，根据TOPS SAR的成像特点，对广义PFA算法进行改进，使其适用于斜视TOPS SAR的数据处理。

2 信号处理与成像方法

2.1 走动校正与PFA插值

斜视SAR存在线性走动，导致距离向与方位向之间具有较强的耦合，线性走动校正可以降低这种耦合性。因此，首先进行走动校正。由式(2)可得，线性走动校正函数为

HLRWC(Kr,ta)=exp(-jKrvsinθ0ta)

(4)

将式(4)与式(1)相乘，可得

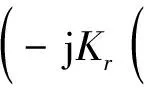
(5)

式(5)中忽略了对成像算法设计没有影响的信号幅度。走动校正后，点目标的距离向聚焦位置将发生偏移，即

Rn=R0+Xnsinθ0

(6)

将式(6)代入式(5)可得

S2(Kr,ta)=

(7)

式(7)中第3个指数项体现了线性距离走动校正引起的方位调频率的空变性，其校正方法将在下一节讨论。完成上述距离走动校正之后，就可进行方位Deramp和二维PFA插值操作，其具体过程参考文献[13]，这里不再赘述。值得注意的是，斜视TOPS SAR模式的有效速度应为vcosθ0，而不是v。

将传统斜视聚束SAR中采用的基于坐标旋转思想的PFA插值和本文线性走动校正后PFA插值进行对比。方位采样示意如图2所示。传统PFA方位向插值采用坐标旋转，即将坐标轴绕合成孔径中心点旋转中心斜视角θ0，如图2(a)所示。原本均匀的采样点A，B，C，D，E变成了非均匀的采样点A′，B′，C，D′，E′，导致方位插值无法采用Chirp-Z变换快速完成。先进行线性走动校正，相当于对回波数据沿距离向进行了人为延迟，将方位向的采样点变为A″、B″、C、D″、E″，如图2(b)所示。由图可见，方位采样点依然均匀，这大大简化了方位向的处理过程。对于线性走动校正引入的方位调频率空变性，可与斜视扫描产生的调频率空变一起校正，不会增加运算量。

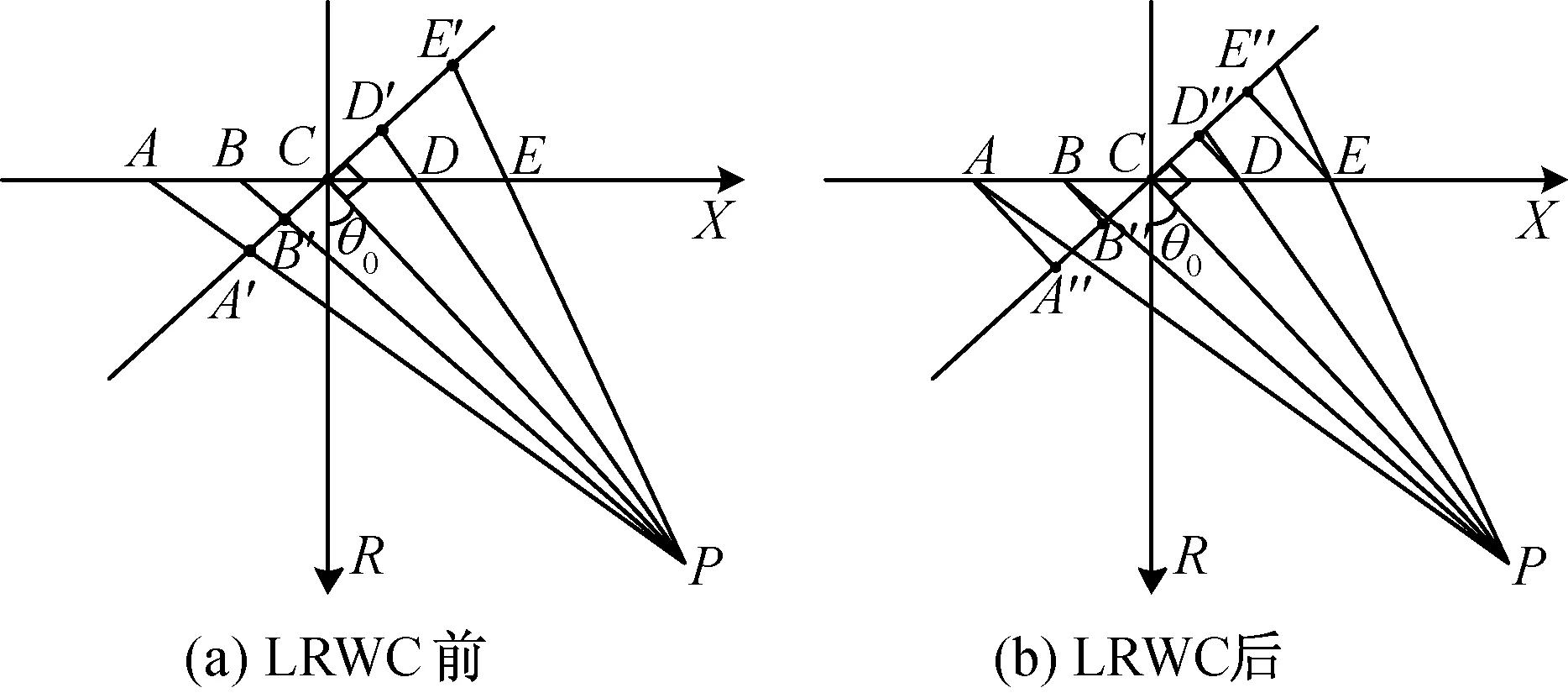
图2 LRWC前后方位向采样间隔Fig.2 Azimuth sampling interval before and after LRWC

2.2 ANCS与方位聚焦

参照文献[12]的方法，在二维插值和函数HQPT补偿后，进行距离向逆傅里叶变换完成距离向的处理，此时信号可表示为

S3(Y,Kx)=sinc(Y-Ynsinθ0)exp(-jKxXncosθ0)·

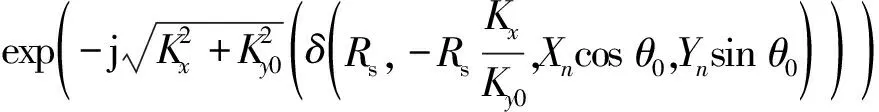
(8)

式中：Kx为方位波数；Ky0为插值后距离波数Ky的中间值；Xn，Yn为成像场景点的坐标；δ为展开量和真实斜距间的误差。式(8)最后的相位项是由LRWC处理导致的剩余多普勒调频率，与目标的方位位置有关。对于TOPS SAR，若直接对插值后的数据进行方位傅里叶变换成像，则所得图像将发生方位混叠[6,13]。为了避开方位混叠，方位变标函数被引入到方位聚焦中，其表达式为

(9)

式(9)为方位波数Kx的二次项，即变标过程中在方位向引入了1个新的调频率，这为ANCS的实现提供了必要的前提。

走动校正后，处于同一距离单元内点目标的方位多普勒调频率为

(10)

式中：θ为TOPS SAR天线波束方位向扫描引起的多普勒调频率变化值，θ=θs+ωta；Xn为线性走动校正引入的方位调频率空变，其表达式为

(11)

因此，点目标P与场景中心点处的调频率差为

Δka(θ,Xn,RB)=

ka(θ,Xn,RB)-ka(θ0,0,RB)

(12)

通过多项式拟合，Δka表示为

(13)

式中：N为采用多次项拟合的次数；An为拟合得到的第n次项的系数。根据式(13)，并借鉴文献[13]的方法，通过二次积分就可得到ANCS扰动函数的相位，即

(14)

因此，扰动函数

HANCS=exp(-jφ)

(15)

将式(15)、式(9)乘到式(8)中，此时，信号的多普勒调频率已不再随目标的方位位置变化，即空变性得以消除。将所得信号转换到方位空域，即

S4(Y,X)=sinc(Y-Ynsinθ0)·

(16)

在方位空域构造相位补偿函数对式(16)进行聚焦，相位补偿函数为

(17)

式(17)补偿后，对所得结果进行方位向傅里叶变换，实现目标聚焦。需要注意的是，本文方法采用了LRWC和PFA算法，忽略了波前弯曲，所得成像结果存在几何形变，最后还需进行形变校正处理。算法流程如图3所示。图中函数Hde，HQPT，Hp的形式为[12]

jKr(Rs-Rrot))

(18)

(19)

(20)

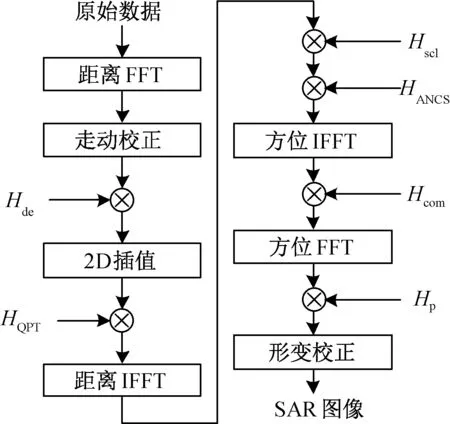
图3 所提算法流程Fig.3 Flowchart of proposed algorithm

3 仿真和实测数据处理

3.1 仿真数据处理

仿真实验中，系统工作在斜视TOPS SAR模式，仿真参数见表1，仿真场景为5×5的矩形点阵，均匀分布在6 km×6.8 km(距离向×方位向)的范围内，如图4所示。

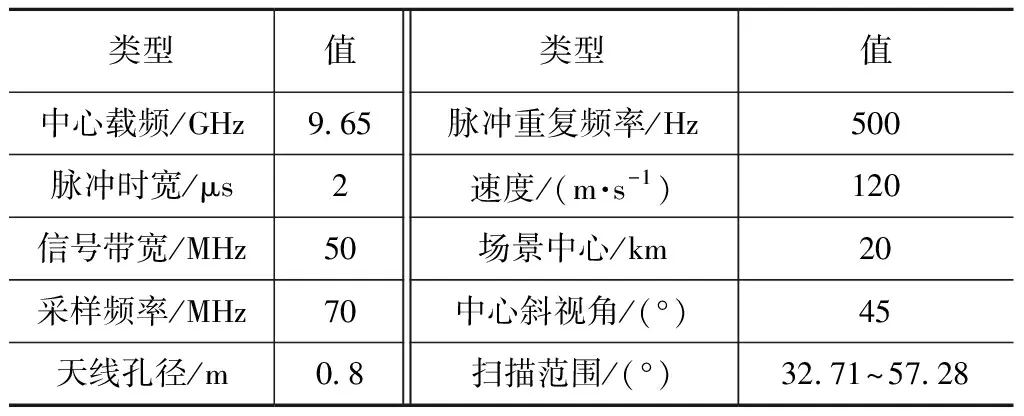
表1 仿真参数Tab.1 Simulation parameters

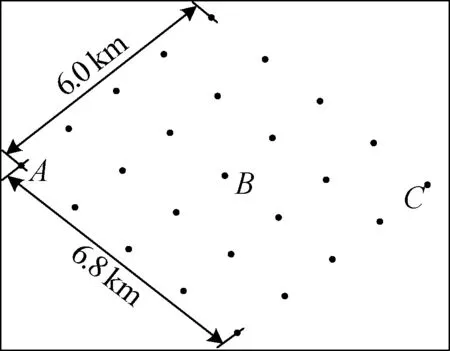
图4 仿真点目标几何示意图Fig.4 Geometry of simulated point targets

采用本文方法所得的成像结果如图5所示。图中：水平方向为方位向，垂直方向为距离向，上端表示场景近端。图5(a)为几何形变校正前的成像结果，图5(b)为几何形变校正结果。由图可见，成像结果未模糊，场景中所有点目标均聚焦良好。

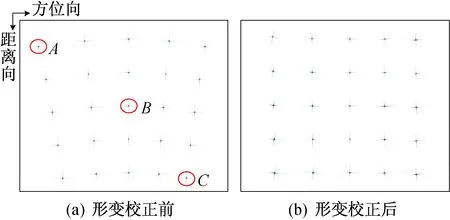
图5 仿真结果Fig.5 Simulation results

为了进一步验证成像性能，图6给出了图5(a)中A，B，C三点的等高线图。表2对该三点的成像性能参数进行了统计，其中：PSLR为峰值旁瓣比，ISLR为积分旁瓣比。由此可见，无论是场景中心点还是边沿点，成像性能均与理论值接近，这进一步表明成像效果良好。

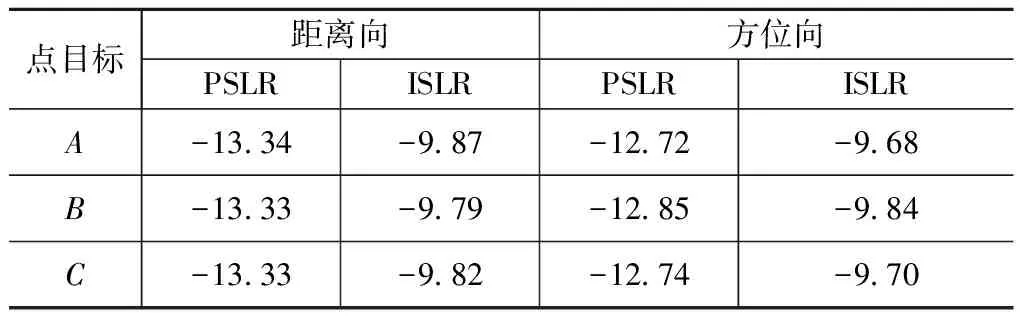
表2 点目标成像性能参数Tab.2 Imaging parameters of focused targets dB

为说明ANCS操作的必要性，图7给出了未进行ANCS处理的斜视TOPS SAR成像结果。对比图6可以看出，虽然场景中心点聚焦较好，但由于方位调频率的空变问题未解决，场景边沿点目标出现了严重散焦。结果表明：ANCS处理可有效消除调频率的方位空变性，提高方位向的聚焦深度，扩大可良好聚焦的场景范围。

图6 点目标A-C等高线图Fig.6 Contour plots of targets A-C

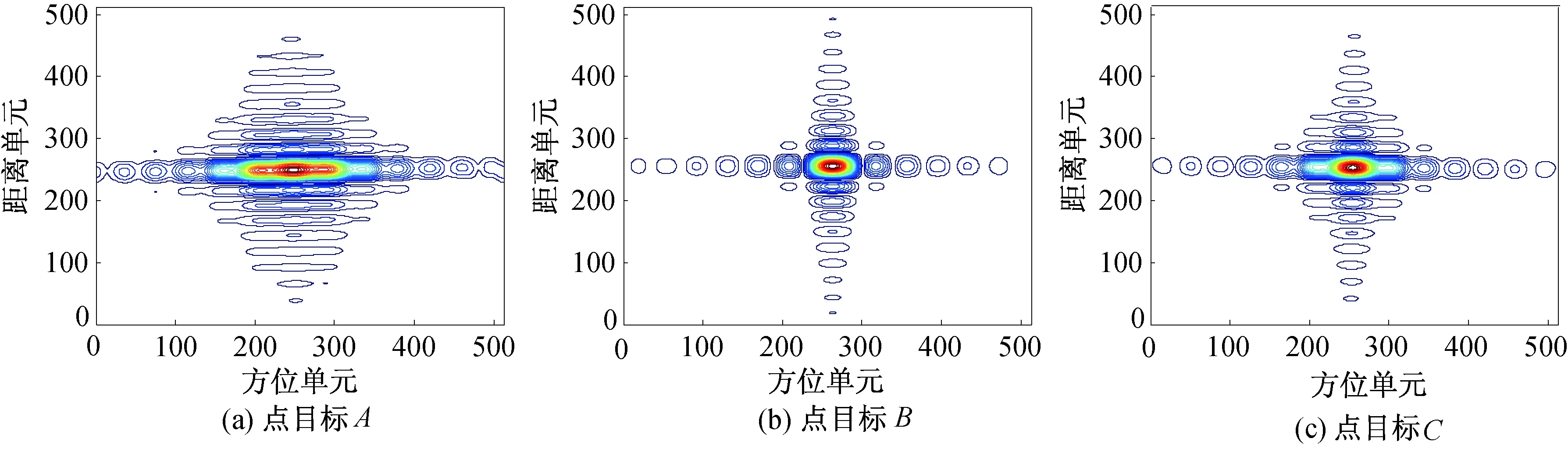
图7 未进行ANCS处理的成像结果Fig.7 Imaging results without ANCS

3.2 实测数据处理

斜视TOPS SAR原始数据为某研究所2010年采集的数据，其主要参数如下：雷达工作在Ku波段，载机速度为70 m/s，发射信号带宽为100 MHz，场景中心距离为8 km，旋转中心距离为-306 m，PRF为1 kHz，中心斜视角为46.15°，扫描范围为34.45°～57.64°。图8为采用本文改进PFA算法成像并形变校正后的结果，图像分辨率约为7.2 m×8.3 m(距离向×方位向)。图中未出现模糊现象，主要目标显示清晰，聚焦效果良好。

图8 机载斜视TOPS SAR实测数据成像结果Fig.8 Imaging result from airborne squinted TOPS SAR real data

4 结论

斜视TOPS SAR由于回波信号的距离向与方位向具有较强的耦合，波束方位扫描导致多普勒调频率空变，成像过程复杂。为此，对广义PFA算法进行了改进，利用TOPS SAR数据方位聚焦的特点，提出先线性走动校正、后PFA插值的步骤。区别于传统聚束SAR采取坐标旋转思想进行的插值，斜视TOPS SAR回波信号经过线性走动校正后，方位采样依然均匀，因此，方位向插值过程可采用Chirp-Z变换快速实现。对于波束扫描及走动校正引起的方位调频率空变问题，结合TOPS SAR聚焦流程，采用ANCS方法进行统一校正，大幅提高了方位向聚焦深度，扩大了可良好聚焦的场景范围。仿真和实测数据验证了本文方法的可行性。与常规PFA算法类似，本文方法也忽略了波前弯曲，因此今后将对波前弯曲有效补偿的方法进行重点研究。