一种可用于预白化类空时自适应处理中的阵元误差校正算法
方 明,李 礼,蔡天祥,赵婵娟,于守江
(上海航天电子技术研究所,上海 201109)
0 引言
与地基雷达相比,机载雷达在下视工作时,由于平台位置的升高增加了雷达的可视距离,尤其是对于低空和超低空突防目标,其可视距离更是大大增加。但随着雷达架设到移动平台,其杂波具有空时二维的耦合特性,此时单从时域或空域很难将杂波滤除干净。在这种背景下,BRENNAN等[1]于1973年提出了空时自适应处理(STAP)技术,通过阵元和脉冲2域的联合处理,极大改善了雷达对慢动目标的检测能力。传统的STAP技术需通过一定数量的独立同分布(IID)训练样本来估计检测单元的杂噪协方差矩阵(CCM)。一般称输出信干比相对于最优滤波器的损耗小于3 dB所需的训练样本数为CCM估计的收敛速度。根据文献[2]可知,传统STAP的收敛速度为2倍空时滤波器维数。但在实际中,由于杂波分布的非均匀性(如地形、地貌的空间变化,人造建筑等强散射点,海陆交界等),2倍空时滤波器维数的IID训练样本往往难以保证,从而导致STAP性能急剧下降[3-8]。
近年来,国内外学者发现,若能充分发掘探测环境的先验知识并加以利用,则能有效克服杂波的非均匀性,从而改善STAP算法的杂波抑制性能[9-12]。因此,这种知识辅助空时自适应处理(KA-STAP)技术逐渐成为研究热点。文献[9-10]分别利用数字地形高程数据、地面覆盖/地面使用数据等先验知识选取与环境相匹配的自适应滤波器和均匀的训练样本,属于间接法。文献[11-12]利用先前的观测数据或其他方式获取当前检测单元的先验协方差矩阵,并将其与观测数据进行融合,以捕捉检测单元的瞬时特征,属于直接法。直接法的基本思想是根据WARD的杂波模型[13],构造先验协方差矩阵对回波数据进行预白化,降低杂波的秩,从而提高系统的收敛速度,故此类算法被统称为预白化类STAP,且在先验协方差矩阵准确时,具有极高的收敛速度。但在相控阵雷达系统中,由于加工装配精度的限制、器件特性的差异,以及阵元间的相互影响,各个阵元间的误差总是难以避免,这直接影响了先验协方差矩阵的估计精度,进而导致预白化类STAP算法性能严重下降。
本文分析了阵元误差对预白化类STAP的影响,提出了一种基于杂波回波数据的阵元误差校正算法。该算法首先将阵元误差建模为方位依赖的幅相误差;然后将空间中各个方位的主瓣杂波作为校正源,利用其阵列输出协方差矩阵的Toeplitz结构会在阵元误差影响下发生改变的特性,估计相应方位的幅相误差;最后利用估计的幅相误差校正先验协方差矩阵和假定目标的导向矢量。试验结果验证了本文算法的有效性。
1 信号模型和阵元误差对预白化类STAP的影响
1.1 信号模型
图1为雷达的观测几何示意图。
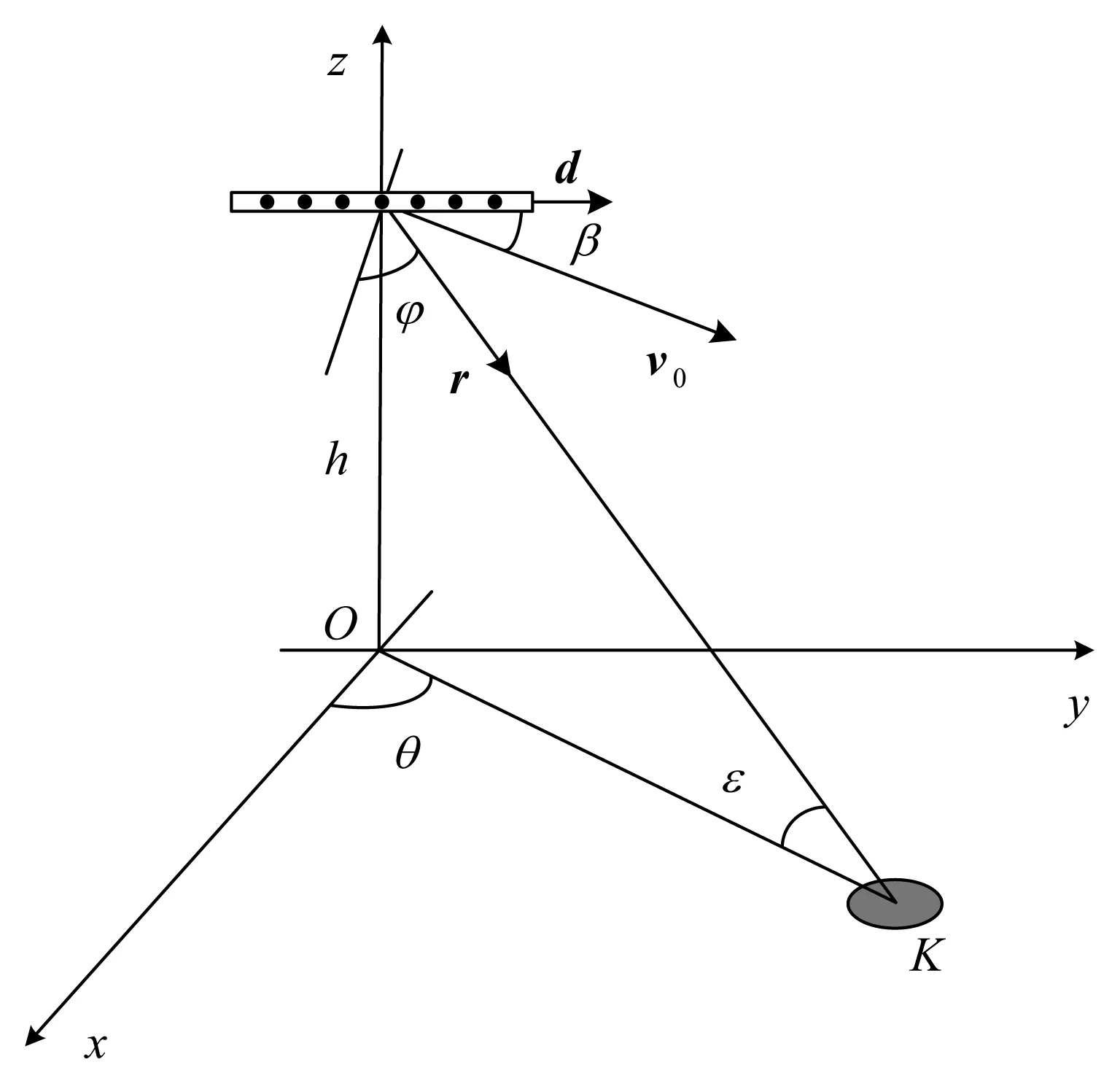
图1 雷达的观测几何示意图Fig.1 Geometric diagram of radar observations
图中:v0为载机速度;β为天线轴与载机速度的夹角;φ为天线轴法线与杂波块K的夹角;ε为杂波块相对于天线的掠射角;θ为方位角;h为载机高度。令r为雷达指向杂波块K的单位向量,rn为第n个阵元的位置,可分别表示为
r=cosεcosθex+cosεsinθey-sinεez
(1)
rn=nd,n=0,1,…,N-1
(2)
式中:ex,ey和ez分别为对应于x,y和z轴的单位向量;d=d·ey,其中,d=λ/2为阵元间距,此处,λ为雷达的工作波长。若设雷达一个相干处理间隔(CPI)内的脉冲数为M,脉冲重复间隔为Tr,则当波束指向ψω时,杂波的回波信号可表示为
⊗a(φi)
(3)
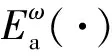
b(φi)=[1,ej2πνi,…,ej2πνi(M-1)]T
(4)
a(φi)=[1,ej2πui,…,ej2πui(N-1)]T
(5)
式中:νi和ui分别为归一化多普勒频率和空间频率,具体形式分别为
νi=2v0·r/λ·Tr=
2v0/λ·sin(θi+β)cosεi·Tr
(6)
ui=d·r/λ=
d/λ·sinφi=d/λ·sinθicosεi
(7)
式(3)是理想情况下的杂波模型,但在实际阵列接收系统中,各个阵元间的误差总是难以避免,因此必须对式(3)进行修正。本文考虑阵元互耦效应、阵元幅相误差和阵元位置误差同时存在时的情况。
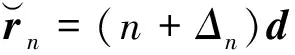
(8)
式中:
ej2π/λ·(N-1+ΔN-1)dsin φi]T
(9)
式(8)可进一步表示为
(10)
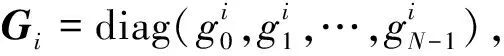
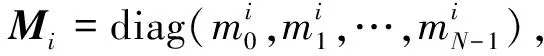
(11)
最后,当波束指向ψω时,实际杂波信号可表示为
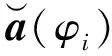
(12)
1.2 阵元误差对预白化类STAP算法的影响
与传统的基于统计信号处理的STAP算法相比,预白化类STAP算法将原有的单线性约束最小化功率输出问题转化为多约束最优化问题。该类算法的本质是先在干扰的位置上通过静态方向图加权对其预置零后,再进行常规自适应处理[14]。色加载(CL)[15]是典型的预白化类STAP算法,该算法在先验协方差矩阵与真实协方差矩阵相同时,具有极高的收敛速度。因此,本文将以CL为例分析阵元误差对预白化类STAP算法的影响。
预白化类STAP算法中的先验协方差矩阵可按式(13)构造,即
(13)
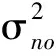
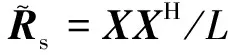
(14)
式中:κ为CL因子,其值取决于先验协方差矩阵R0的估计精度。
最终,空时二维滤波器的权系数可表示为
(15)
式中:s=bt⊗at为假定目标的空时导向矢量。其中:bt=[1 ej2πνt… ej2πνt(M-1)]T为目标的时间导向矢量,此处,νt=(2vt/λ)·Tr为目标的归一化多普勒频率,vt为目标相对雷达的径向速度;at=[1 ej2πut… ej2πut(N-1)]T为目标的空间导向矢量,此处,ut=(d/λ)·sinφt,φt为目标与天线法线的夹角。
为研究阵元误差对CL算法的影响,将式(14)重写为
(16)
式中:预白化后的样本协方差矩阵
(17)
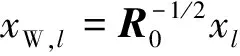
在理想情况下,利用式(14)估计的杂波子空间可很好地逼近实际接收数据的杂波子空间,故预白化后的杂波子空间较小,算法很快收敛。但是,在实际接收阵列中,由于阵元误差的存在,杂波子空间的估计精度降低,这导致预白化后的杂波子空间较大,最终使CL算法的收敛速度变慢。此外,构造空时滤波器时,阵元误差会使假定的目标导向矢量与实际的目标导向矢量失配,造成目标信号部分相消,进一步降低CL算法的收敛速度。
因此,对于预白化类STAP算法,为保持较高的收敛速度,必须校正阵元误差。
2 阵元误差校正
当前的误差校正算法主要分为有源校正和自校正2类。有源校正是指在空间设置辅助源对阵列误差参数进行离线估计。因自校正不需要辅助源,可实时在线完成误差校正,应用方便,故较适合机载平台。由1.1节可知,当阵元同时存在幅相误差、位置误差和互耦效应时,可将其视为方位依赖的幅相误差,即阵列在不同入射角下具有不同的幅相误差。因此,为得到较为精确的杂波子空间估计,必须估计各个入射方向的阵元幅相误差。因机载雷达各个方位都存在地杂波,故考虑将地杂波作为校正源。
假设空间中存在一个入射角为ψω的校正源,对于N元的均匀线阵,在无误差条件下,阵列的输出协方差矩阵可表示为
P=(pkl)=ej2π(k-l)d/λsin φω
(18)
式中:pkl表示矩阵P第k行第l列的元素;P具有Toeplitz结构。
当存在方位依赖的幅相误差时,协方差矩阵可表示为
(19)
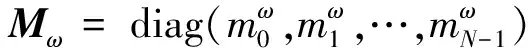
(20)
(21)
由式(18)~(21)可知,如果阵列各个入射方向都存在校正源,且可得到其阵列输出协方差矩阵,则可通过式(20),(21)得到各个入射方向的幅相误差估计。基于这样的思考,本文将雷达天线指向空间各个方位时的主瓣杂波作为校正源,利用主瓣杂波的输出协方差矩阵的Toeplitz结构会在阵元误差的影响下发生改变这一特性来估计各个入射方向的阵元幅相误差。
然而,天线某一指向的回波数据不仅包含该方向的主瓣杂波,其他方向的杂波也会从天线的旁瓣进入,进而影响相应入射方向的幅相误差估计。为减轻旁瓣杂波对幅相误差估计的影响,本文先对每个方位的回波数据进行多普勒滤波,旨在进一步压低旁瓣杂波的功率水平。
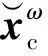
(22)
式中:Tω=Fω⊗IN。
相应的输出协方差矩阵的估计为
(23)
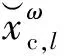
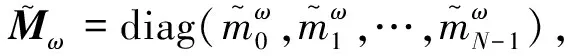
最后利用各个入射方向的幅相误差估计修正先验协方差矩阵和目标的空时导向矢量,即
(24)
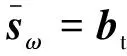
(25)
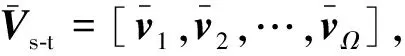
3 仿真试验与结果分析
本节利用仿真数据来验证本文算法的有效性。
将阵元的幅度误差、相位误差和位置误差定位分别定义为
An=1+δaξn
(26)
φn=1+δpζn
(27)
Δn=1+δlχn
(28)
式中:ξn,ζn和χn为服从标准正态分布的随机变量;δa=0.2,δp=12°和δl=0.05λ分别为幅度误差、相位误差和位置误差的标准差。
仅考虑最近邻3个阵元之间的互耦效应,可将互耦矩阵设为
C= Toeplitz[1,0.15+0.13j,-0.03-0.04j,
0,…,0]
(29)
为定量衡量阵元误差校正算法的性能,将入射角为ψω时的幅度误差估计均方误差和相位误差估计均方误差分别定义为
(30)
(31)
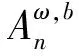
本文采用信干比损耗来衡量STAP算法的杂波抑制性能,其定义为输出信干比和相同自由度下白噪声中匹配滤波器的输出信噪比的比值,即
(32)
雷达的发射信号为线性调频信号,其系统参数见表1,平台参数见表2。
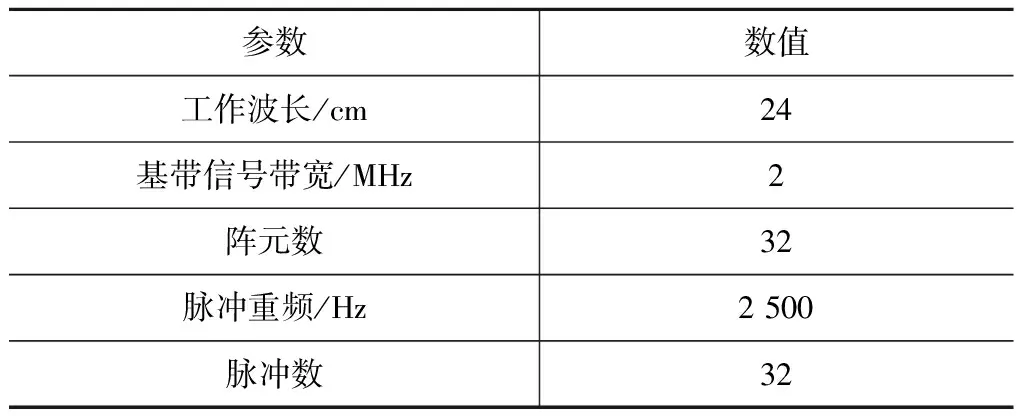
表1 雷达的系统参数Tab.1 System parameters of radar
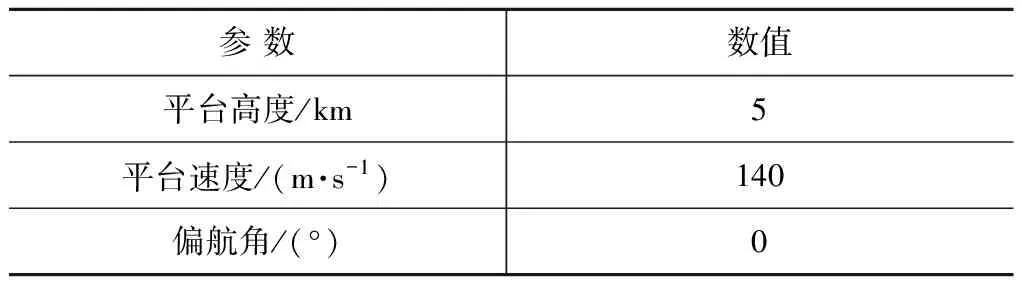
表2 平台参数Tab.2 Platform parameters
3.1 阵元误差对CL收敛速度的影响
CL技术在先验协方差矩阵准确时具有极高的收敛速度,但当存在阵列误差时,若不进行相应处理,则其收敛速度会大大降低。本文通过仿真试验考察阵元误差对CL收敛速度的影响。试验时,CL算法的先验协方差矩阵可按式(13)构造,假设杂波块的多普勒频率、空间频率和强度都精确可知,且加载因子为最小均方误差意义下的最优加载因子[19]。运动目标的到达角为0°,径向速度为-15 m/s。
理想情况下预白化前和预白化后回波信号的杂波功率谱(单位为dB)如图2所示。从图中可以看出,当先验协方差矩阵精确可知时,预白化后回波中的杂波被抑制到噪声水平。但是,当阵列存在误差时,预白化后杂波的功率谱(单位为dB)依旧较高,如图3所示。
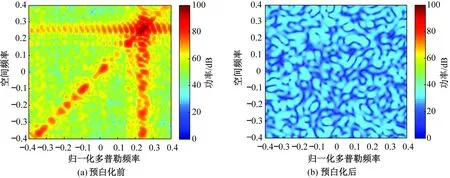
图2 理想情况下预白化前后回波信号的杂波功率谱Fig.2 Clutter power spectrum of echo signals before and after pre-whitening in ideal pre-whitening condition
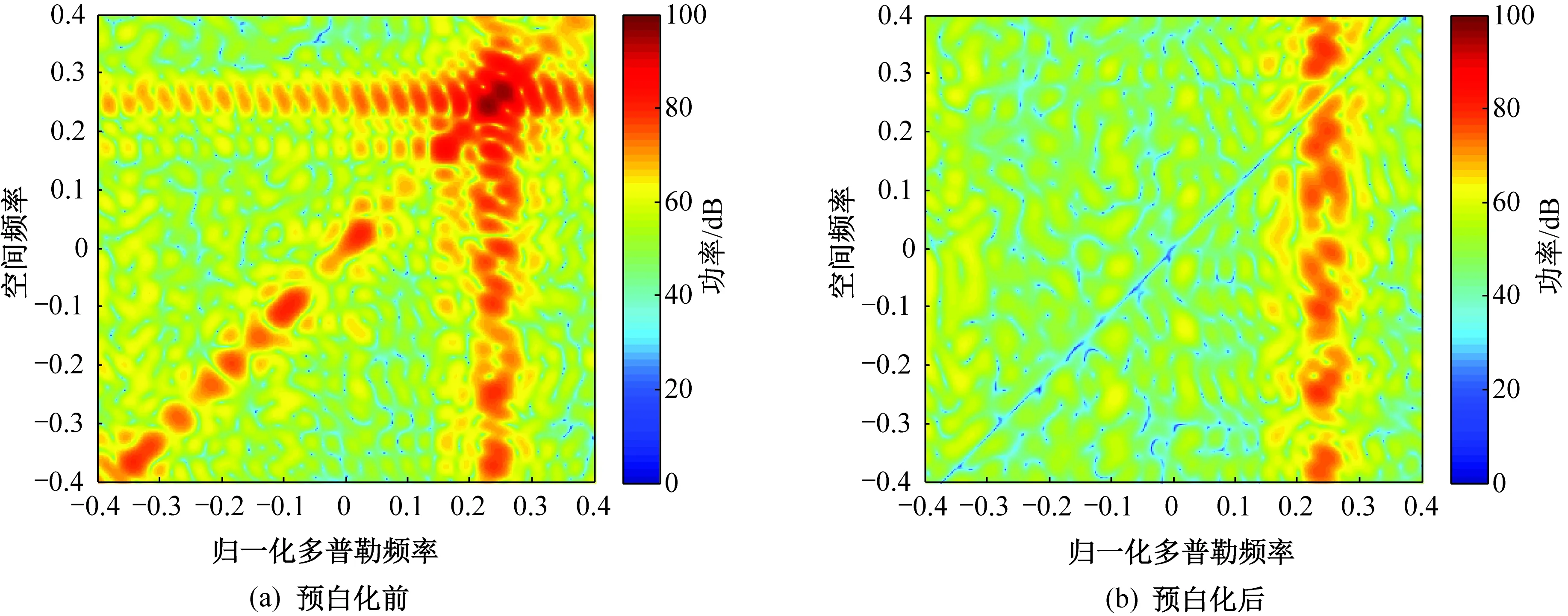
图3 存在误差时预白化前后回波信号的杂波功率谱Fig.3 Clutter power spectrum of echo signals before and after pre-whitening in presence of errors
CL算法在无误差和有误差时的收敛曲线如图4所示。由图可知:当无误差时,CL算法的收敛速度很快,仅需很少的训练样本即可完成杂噪协方差矩阵的估计;当阵列接收系统有误差时,CL算法需在样本数L≥192的条件下才可获得近似最优的信干比损耗。造成CL算法性能下降的主要原因是阵元误差会使先验协方差矩阵偏离真实的协方差矩阵,导致预白化后的杂波子空间依然较大,进而使准确估计杂噪特性所需的样本数增大。此外,阵元误差会使假定的目标导向矢量与实际的目标导向矢量失配,造成目标能量的部分相消,进一步增大信干比损耗。
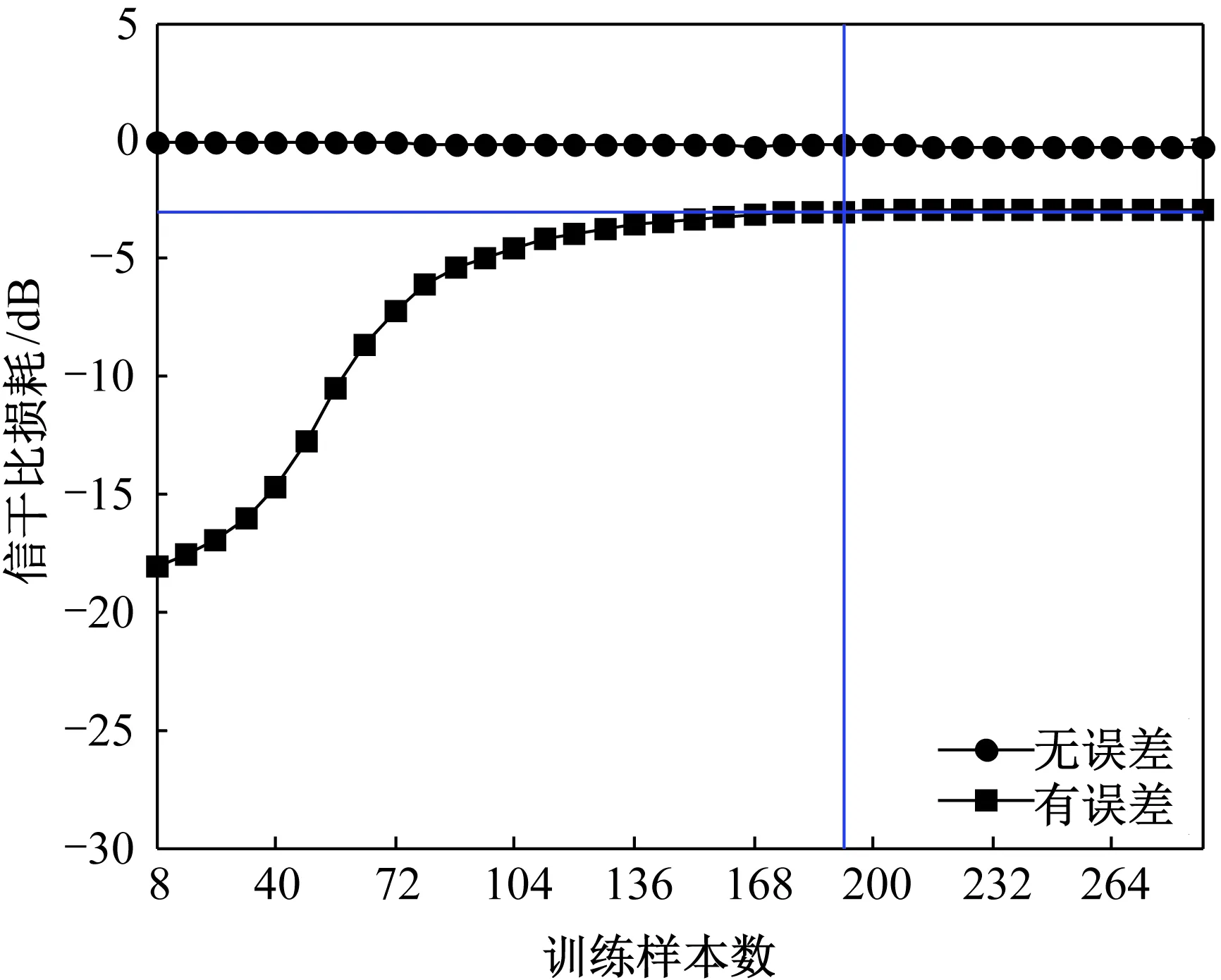
图4 CL算法在无误差和有误差时的收敛曲线Fig.4 Convergence curve of CL algorithm without and with errors
3.2 训练样本数对本文算法的影响
试验设置同3.1节,通过Monte Carlo仿真试验,对阵列在不同入射方向下的幅度误差和相位误差的估计均方误差进行仿真,考察训练样本数对本文算法的影响,得到的试验结果如图5所示。从图中可以看出,本文的校正算法确实能校正阵列各个波达方向的幅相误差,且当训练样本数大于64时,所有方向的相位误差估计精度均能控制在1.2°以内,而幅度误差估计精度在7%以内。
3.3 本文算法在CL算法中的应用
为进一步验证本文算法的有效性,将阵列误差校正算法应用到CL算法中。试验时,假设杂噪比为40 dB,训练样本数为64,得到的试验结果如图6所示。由图可知:存在阵元误差时,若不对其进行处理,则CL算法在旁瓣杂波区的信干比损耗超过-8 dB;采用本文算法校正阵元误差后,CL算法在旁瓣杂波区的信干比损耗被控制在-2 dB以内。这进一步验证了本文算法的有效性。
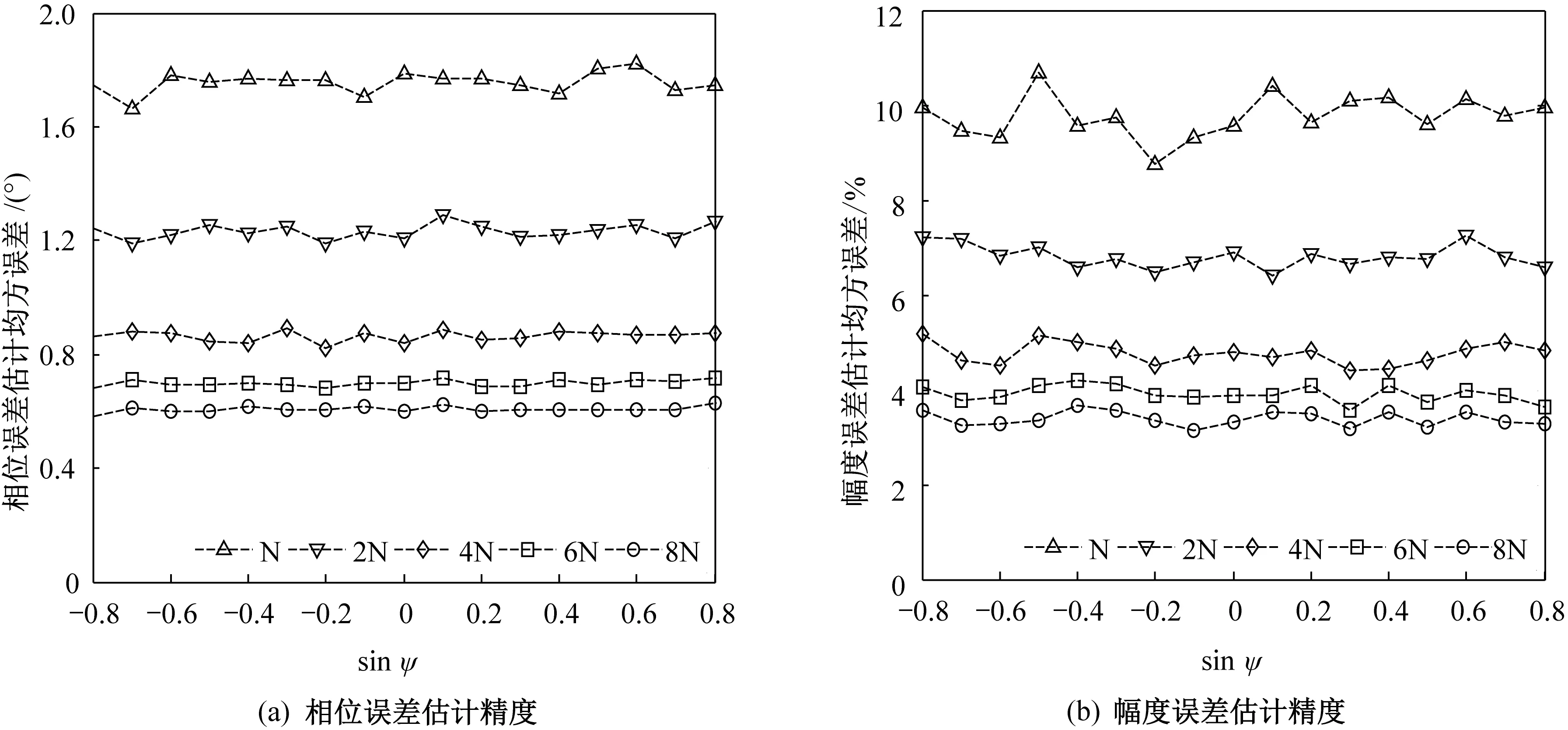
图5 本文算法在不同样本数下的性能曲线Fig.5 Performance curves of proposed algorithm under different sample sizes
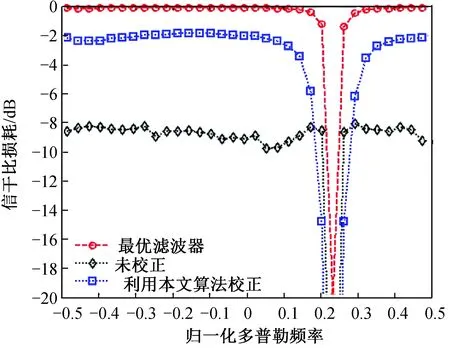
图6 CL算法在阵元误差校正前后的信干比损耗Fig.6 Signal to interference ratio loss of CL algorithm before and after array error correction
4 结束语
本文分析了阵元误差对预白化类STAP的影响,提出了一种基于杂波回波数据的阵元误差校正算法。具体而言,首先将阵元误差表示为方位依赖的幅相误差;然后,将空间中各个方位的主瓣杂波作为校正源,利用其阵列输出协方差矩阵的Toeplitz结构会在阵元误差影响下发生改变的特性估计相应方位的幅相误差;最后,利用估计的幅相误差校正先验协方差矩阵和假定目标的导向矢量。仿真结果表明:存在阵元误差时,本文所提的阵元误差校正算法可明显改善预白化类STAP算法的杂波抑制性能。
该误差校正算法主要针对均匀线阵,然而随着雷达技术的不断发展,未来机载雷达一个重要的趋势是采用共形阵,因此如何对共形阵进行误差校正有待后续研究。

