投资组合中协方差阵的估计和预测

刘丽萍

（贵州财经大学数学与统计学院，贵阳 550025）

引言

协方差阵在实际生活中有着广泛的应用，尤其是在资产组合及风险管理中，其扮演着不可替代的角色。协方差阵的估计方法大都是基于低频数据的。近年来，高频数据越来越容易获得，较低频数据而言，其包含了更加丰富的信息。高频数据的信息量更高，但抽样频率提高的同时会带来微观噪声影响越来越大的问题。由于短期内的价格波动等因素，资产收益率可能出现幅度较大的变化，数据呈现跳跃状态，该跳跃对高频数据协方差阵估计带来更多难题。信息技术的发展促使更多高频交易场景以及更高频率的交易场景的出现。人们对高频协方差阵的研究也随之深入，对微观噪声和跳跃对其估计的影响也进行了探索。研究指出，微观噪声以及跳跃存在时，积分协方差阵的一致估计量不是已实现协方差阵，并提出降低微观噪声以及跳跃影响的估计量（比如Zhang（2011）[1]、Griffin和Oomen（2011）[2]、Barndorff-Nielsen和Hansen等（2011）[3]、以及Nole和Voev（2008，2012）[4～5]）。但之前的研究往往分别研究噪声或者跳跃的影响，刘丽萍（2013）[6]提出了修正的门限预平均已实现协方差阵（MTPCOV），MTPCOV估计量同时考虑了噪声和跳跃的影响，以期弥补之前研究的不足。

频率高、维度大是当今金融机构所研究的数据的显著特征。这种情况下，维数诅咒导致一些协方差阵的估计和预测模型的适用性较差。为了克服这些问题，本文将MTPCOV和VAR-LASSO结合起来，来解决噪声、跳跃和维数诅咒对协方差阵估计的影响。本文后续内容如下：第一部分详细介绍了MTPCOV估计量；第二部分将MTPCOV和VAR-LASSO模型相结合来估计和预测高维高频的金融协方差阵；第三部分是实证分析；最后一部分是本文的结论。

一、MTPCOV估计量

修正的门限预平均已实现协方差阵（MTPCOV）是由刘丽萍（2013）[6]提出的，其构造形式如下：

在上式（1）中，由马丹和尹优平（2012）[7]的研究可知，MTPCOV的主对角线元素MTPRV的形式为：

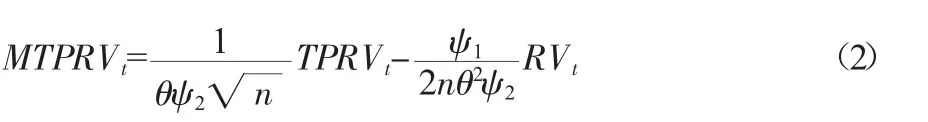
由刘丽萍（2013）[6]的研究可知，MTPCOV的副对角线元素MTPCV的形式为：

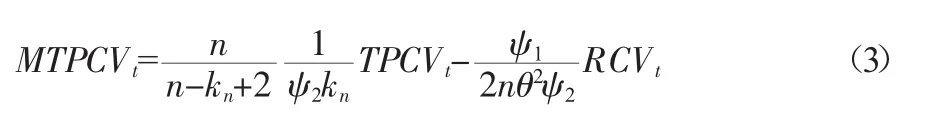
刘丽萍（2013）[6]的研究指出，协方差阵MTPCOV解决了维数诅咒和噪声的影响，是积分协方差阵的一致估计量。但是，当资产的维度较高时，该估计量将面临着严重的维数诅咒问题，估计效果很差。为此，本文考虑将MTPCOV估计量和VAR-LASSO模型相结合，来解决维数诅咒问题。

二、考虑噪声和跳跃影响的高维高频协方差阵的估计和预测

前文提到的MTPCOV估计量同时考虑了噪声和跳跃的影响，但是当资产的维度较高时，该估计量将面临着严重的维数诅咒问题。为此，我们考虑将MTPCOV估计量和VAR-LASSO模型相结合，首先采用MTPCOV估计量估计出高频数据的协方差阵，将其记为∑。VAR-LASSO模型是由Callot和Kock等（2017）[8]针对高维高频数据而提出的模型，该模型认为，前p期的协方差阵的值会影响到当期的值。也就是说，第t期的协方差阵∑t依赖于∑t-1，…，∑t-p。假定资产的维度为n，则协方差阵∑t为n×n，共有不同元素n（n+1）/2个。对采用MTPCOV估计量估计的t时期的协方差阵∑t的上三角元素进行拉直操作，符号vech（）表示拉直操作，得到向量yt=vech（∑t）。假定yt服从VAR（p）模型，即：

式（4）中，Φi（i=1，…，p）是k×k的系数矩阵（k=n（n+1）/2）；yt-i=vech（∑t-i）。式（4）可以简化为如下形式：

式（4）中，yi=（yT，i，…，y1，i）′是观测值i（i=1，…，k）的向量；єi=（єT，i，…，є1，i）′是由对应的残差构成的向量；X=（ZT，…，Z1）′，是kp维的系数向量。根据式（5）可知，我们所建立的每一个方程，都需要估计个个参数，并且待估参数的个数会随着资产产维度的增加而急剧地增加，资产维度的增高会加剧式（5）的估计困难。所以，Callot和Kock等又进一步在VAR（p）模型中引入LASSO方法，将不显著变量的回归系数压缩至0。其思想可以由式（6）表示，通过最小化式（6）来估计最优的回归系数。

估计出VAR-LASSO模型的回归系数后，便可以根据其进一步做预测，假定我们做的是滚动的一步向前预测。则：

三、实证研究

在该部分的实证研究中，我们选择的是2011年1月4日至2014年9月30日的上证180指数成份股的高频数据，剔除交易缺失的数据，共有交易的天数为906天。将906天划分为估计和预测两个部分，估计区间的长度为806天，预测区间的长度为100天。采用滚动预测法来预测后100天的协方差阵。首先采用MTPCOV和Andersen（2003）[9]提出的RCOV估计量来估计前806天的协方差阵，接着采用VAR-LASSO模型和刘丽萍等（2015）[10]提出的CF-ARMA模型来预测第807天的协方差阵；然后采用相同的协方差阵估计量来估计2—807天的协方差阵，从而预测出第808天的协方差阵；依此类推，直到选用101—905天的数据来估计协方差阵，最后预测出第906天的协方差阵。我们将预测出的100天的协方差阵应用在投资组合中，来验证它的应用效果。这里，我们采用的投资组合是等比例风险投资组合。下表给出了我们采用不同的模型预测得到的资产组合的收益、波动和夏普比例值。

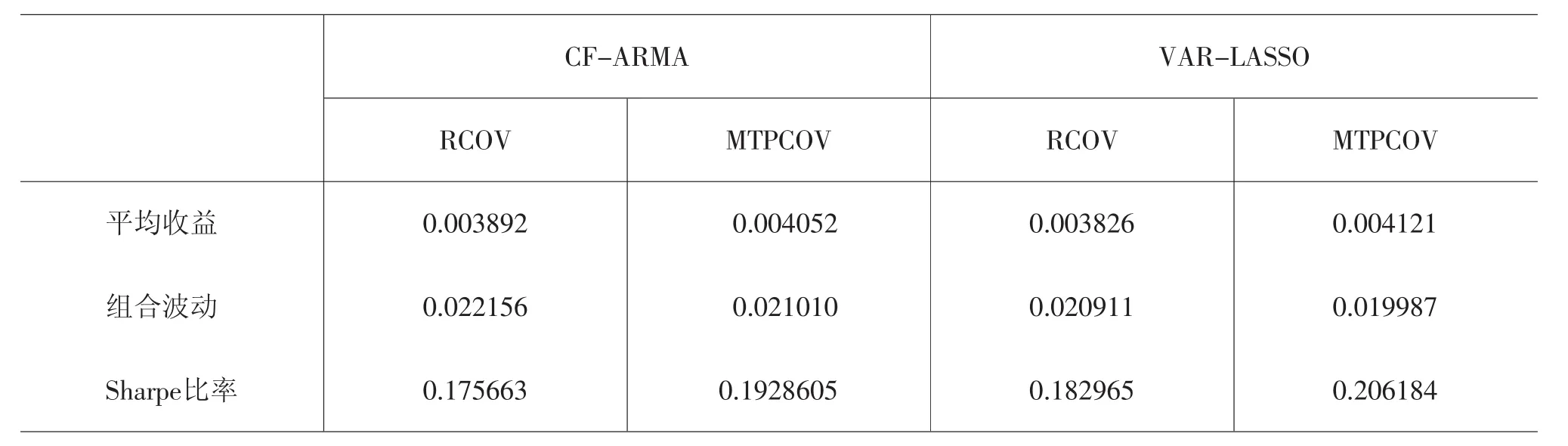
组合收益、波动及Sharpe比率值

从上表可以得到三条结论：首先，无论采用的预测模型是CF-ARMA模型还是VAR-LASSO模型，由MTPCOV估计量构造的投资组合的收益明显高于RCOV，并且MTPCOV的组合波动更小，Sharpe比率值更高，这是因为MTPCOV估计量克服了噪声和跳跃的影响。其次，预测模型VAR-LASSO明显要优于CF-ARMA。最后，由VAR-LASSO模型预测的MTPCOV估计量构造的投资组合最优，其对应的Sharpe比率值最高，因为VAR-LASSO模型和MTOCOV相结合来估计和预测金融数据的协方差阵时，不仅解决了噪声和跳跃的问题，还解决了维数灾难问题。

下页图是VAR-LASSO和CF-ARMA模型预测的资产组合的边界图，下页图的结果基本与上表相符，进一步说明考虑了噪声和跳跃的MTPCOV估计量明显优于RCOV估计量，采用VAR-LASSO模型预测的MTPCOV估计量应用在投资组合中有较好的表现。

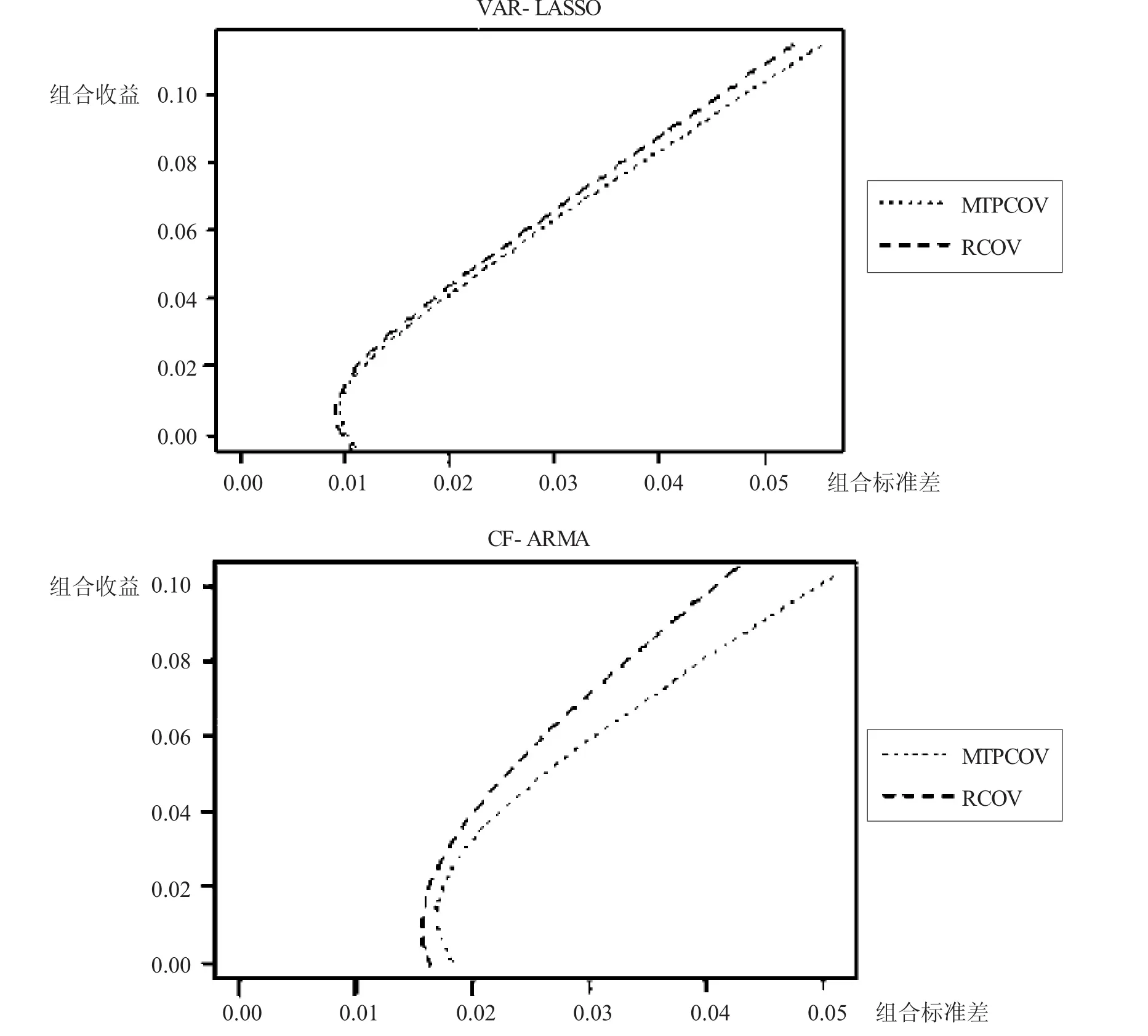
组合的有效边界图

结语

高维高频协方差阵的估计和预测是统计领域研究的热点问题。噪声、跳跃以及维数诅咒问题为协方差阵的估计带来了众多的挑战。本文将MTPCOV和VAR-LASSO模型相结合来来估计和预测高维高频协方差阵，在考虑了噪声和跳跃对协方差阵估计影响的同时，也解决了维数诅咒问题。将VAR-LASSO模型预测的MTPCOV估计量应用在投资组合中，发现与其他估计量相比，由其构造的投资组合有更好的表现，收益更高，风险更小，其对应的Sharpe比率值更高。