InSAR图像配准雷达几何法处理性能分析

路瑞峰，赵 迪,2，侯雨生，陈重华，魏 春，陈筠力

(1.上海卫星工程研究所，上海 201109； 2.中科卫星应用德清研究院浙江省微波目标特性测量与遥感重点实验室，浙江 湖州 313200)

0 引言

干涉合成孔径雷达(InSAR)是获取高精度地面高程模型(DEM)的重要遥感手段[1-3]。它利用沿垂直航向分布的2部SAR天线，以不同视角观测同一地区，并对获取的2幅复SAR图像进行干涉处理，求取主副雷达天线相位中心与目标之间的斜距差，进而获取观测区域的DEM。图像配准是InSAR处理的关键步骤，其精度不仅会影响主辅SAR图像的相干性，在斜视雷达几何下，还会在干涉条纹图中引入相位偏差[4]。提高图像配准精度对提高DEM精度具有重要意义。

目前，国内外对InSAR图像配准进行了深入研究，并提出了多种有效的处理算法，主要包括最大相关系数法、最大频谱法、点目标配准法和雷达几何法[2-7]。前3种方法均基于数据，其配准性能与数据质量密切相关，而基于雷达几何的图像配准方法是一种独立于SAR图像复数据的方法。雷达几何法因其在复杂地形下稳健的配准性能而受到广泛关注[5-7]，但其配准精度与图像几何参数和外部辅助DEM精度密切相关。文献[7]研究了DEM误差对雷达几何法图像配准性能的影响，但没有对图像几何参数精度对算法性能的影响进行分析。

本文从SAR图像雷达几何出发，利用偏微分方程系统研究了SAR几何参数误差、粗DEM精度等非理想因素对雷达几何InSAR图像配准算法性能的影响。本文内容安排如下：第1节介绍了利用雷达几何进行InSAR图像配准的基本原理和处理流程，第2节分析了各非理想因素对SAR图像反定位精度的影响，第3节分析了雷达几何图像配准法对重复航过和单航过InSAR系统的配准性能，最后在第4节对全文进行了总结。

1 基于雷达几何的InSAR图像配准方法

InSAR图像配准雷达几何法主要依据主辅SAR图像的雷达成像距离多普勒几何[6]，即

(1)

|ptarget-pt,i(ta,i)|+|ptarget-pr,i(ta,i)|=cτi

(2)

式中：ptarget为地面目标位置矢量；pt,i(t)和vt,i(t)分别为第i幅SAR图像发射天线相位中心在方位时刻t的位置和速度；pr,i和vr,i分别为第i幅SAR图像接收天线相位中心位置和速度；λ为雷达波长；fdfc,i为第i幅SAR图像成像多普勒中心频率；ta,i和τi分别为该目标对应的方位时间和信号传播时延。在式(1)中，令pt,i(t)=pr,i(t)，vt,i(t)=vr,i(t)，即可得到单基SAR系统的距离多普勒方程。

本文采用地球固定坐标系。当天线相位中心状态矢量和雷达成像参数已知时，可结合地球模型解算目标空间位置，实现SAR图像目标几何定位[8]。常用的地球椭球模型为

(3)

式中：ptarget=[pxpypz]T；Re为地球赤道半径；f为地球扁率因子；h为目标高程。当观测场景内的目标点三维坐标已知时，通过求解式(1)，(2)也可解算出该目标在SAR成像几何下的方位时间和脉冲延迟，此时目标在第i幅SAR图像中的方位和距离坐标(na,i,nr,i)可由式(4)，(5)求得，即

na,i=(ta,i-tas,i)·fp,i

(4)

nr,i=(τi-τs,i)·fs,i

(5)

式中：tas,i和τs,i分别为第i幅SAR图像方位起始时间和距离起始时间；fp,i和fs,i分别为第i幅SAR图像的脉冲重复频率和距离向采样频率。该过程被称为SAR图像反定位。

利用粗DEM求取图像配准偏移量，其基本流程如图1所示，主要包括：

1) 从SAR主图像中，按128格×128格网间距选择图像配准控制点[9]，并提取其雷达成像参数(包括雷达斜距、成像多普勒中心、雷达波长)，以及天线相位中心状态(包括位置、速度)测量信息。

2) 利用RD法根据辅助粗DEM对控制点进行目标定位。

3) 利用辅SAR图像数据录取参数(包括方位和距离起始时间、脉冲重复频率、距离向信号采样频率)，求取目标点在辅SAR图像上的方位和距离向坐标，并据此确定主辅SAR图像方位和距离向配准偏移量。

4) 重复步骤1～3，直至求取出所设全部控制点的配准偏移量。

5) 内插出SAR图像各像素的配准偏移量，并对SAR辅图像进行重采样。

图1 粗DEM辅助InSAR图像配准偏移量求取流程Fig.1 InSAR image coregistration offset extraction process with coarse DEM

2 雷达几何法SAR图像配准误差源及其影响分析

在实际InSAR系统中，利用雷达几何进行图像配准，其主要影响因素有主辅SAR图像天线相位中心状态测量误差、成像处理误差、GPS时间记录误差、电子延迟误差和大气延迟误差引起的斜距误差等SAR图像几何参数误差，以及粗精度DEM高程误差[8]。利用表1中的德国TerraSAR-X系统参数[10]对SAR图像目标反定位精度进行分析。

由式(1)～(5)可知，影响雷达几何法SAR图像配准精度的主要因素包括天线相位中心速度误差、天线相位中心位置误差、控制点位置误差、方位定时误差、斜距误差等，具体分析如下。记

表1 TerraSAR-X卫星典型系统参数Tab.1 Typical system parameters of TerraSAR-X

注：如无特殊说明，仿真中取下视角为28.5°。

Fi(vt,i(ta,i),ptarget,pt,i(ta,i),vr,i(ta,i),pr,i(ta,i),fdfc,i,ta,i,τi)

(6)

Gi(vt,i(ta,i),ptarget,pt,i(ta,i),vr,i(ta,i),pr,i(ta,i),fdfc,i,ta,i,τi)

≜|ptarget-pt,i(ta,i)|+|ptarget-pr,i(ta,i)|-cτi

(7)

由隐函数存在定理可知，Jacobian矩阵为

(8)

式中：

(9)

(10)

(11)

(12)

2.1 天线相位中心速度误差

假定发射和接收天线3轴速度误差分别为Δvt,i和Δvr,i，则该误差引起的目标在第i幅SAR图像中反定位误差为

(13)

式中：

(14)

(15)

(16)

(17)

卫星速度误差对SAR图像反定位精度影响的仿真试验和理论分析结果如图2所示。图中，va和vr分别表示沿航向和沿雷达视线速度，vb=vavr。由图可知，沿视线方向的速度误差影响较大，其他速度分量的影响可忽略不计，而速度误差对距离向反定位精度的影响基本可忽略不计。

图2 速度误差对SAR图像反定位精度影响分析曲线Fig.2 Influence of velocity error on SAR image reverse positioning accuracy

2.2 天线相位中心位置误差

假定发射和接收天线3轴位置误差分别为Δpt,i和Δpr,i，则其引起的目标在第i幅SAR图像中反定位误差为

(18)

式中：

[ptarget-pt,i(ta,i)]

(19)

(20)

[ptarget-pr,i(ta,i)]

这座宫殿其实是一座城堡，墙体很厚，有的地方甚至厚达3米。如果仔细观察，你会发现宫殿正面，位于两侧的圆塔是不一样的——左侧的圆塔较为粗糙，历史印记更明显，这是当年建造的；右侧的圆塔则是后来建造的，为的是追求左右对称的建筑结构，其塔身的颜色明显不同于左侧的圆塔。

(21)

(22)

卫星定位误差对SAR图像反定位精度的影响的仿真试验和理论分析结果如图3所示。由图可知，仿真试验结果和理论分析结果保持一致。SAR图像方位向反定位精度主要受沿航向位置误差影响，其他位置误差分量的影响可忽略不计；而其距离向反定位精度主要受沿视线方向位置误差影响，其他分量的影响可忽略不计。

图3 位置误差对SAR图像反定位精度影响分析曲线Fig.3 Influence of position error on SAR image reverse positioning accuracy

2.3 控制点位置误差

假定主图像中控制点的位置误差为Δptarget，则该控制点在第i幅SAR图像中反定位误差为

(23)

式中：

[ptarget-pt,i(ta,i)]+

[ptarget-pr,i(ta,i)]

(24)

(25)

目前，利用雷达几何法进行SAR图像配准时，常使用数据精度满足DTED-2标准的SRTM DEM，其格网间距为90 m，地面绝对高程精度为15 m。该DEM在大地坐标系下，使用时需转化至地球固定坐标下。大地坐标系到地球固定坐标系的转换公式为

(26)

式中：(L,B,h)为目标大地坐标系坐标，L，B和h分别为其经度、纬度和高程；N为地球纬度圈半径；e2=1-(1-f)2，为地球第二曲率的平方；Req为地球赤道半径。由式可知，目标位置误差与高程误差的关系为

(27)

由式(1)，(2)可知，目标位置误差可等效为卫星位置误差，其影响不再赘述。由式(27)可知，在雷达几何法图像配准中，目标位置误差由目标高程误差引起，且与目标空间位置有关。在一个轨道周期内，TerraSAR-X卫星15 m高程误差引起的SAR图像反定位误差仿真试验结果如图4所示。由图可知，高程误差主要引起距离向反定位误差。

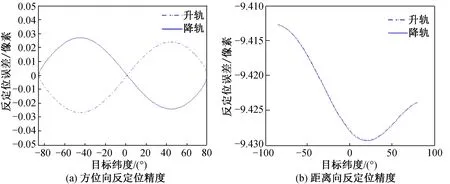
图4 高程误差对SAR图像反定位精度影响分析曲线Fig.4 Influence of DEM error on SAR image reverse positioning accuracy

2.4 方位定时误差

方位定时误差(ΔtGPS,i)来自GPS时间同步误差和卫星频率源误差，直接影响SAR图像中点目标的方位位置，方位定时误差对目标位置的影响可表示为

(28)

2.5 斜距误差

雷达斜距误差主要来自电子电路延迟和大气延迟。斜距误差对目标位置的影响可表示为

(29)

式中：Δτe,i为电子电路延迟；Δτatm,i为大气延迟。

综上所述，目标点在第i幅SAR图像中的位置误差可表示为

(30)

3 基于雷达几何的InSAR图像配准性能分析

对基于雷达几何的图像配准算法性能，可采用以下流程进行分析：首先，分析主图像目标定位误差Δptarget，然后将其作为分析辅图像反定位误差的输入，利用式(30)求出SAR辅图像反定位精度，即可求得该算法的配准精度。为降低分析复杂度，本文采用误差已知的地面控制点(如粗DEM)分析其在主辅SAR图像中的反定位精度，并据此分析该算法精度。从统计意义上讲，上述2种方法是等价的。本文根据第i,j幅SAR图像求取配准偏移量误差的表达式为

(31)

式中：Δna_regis为方位向配准偏移量误差；Δnr_regis为距离向配准偏移量误差。为便于下面分析，这里将天线相位中心位置误差、天线相位中心速度误差、GPS时间误差和雷达斜距误差归结为图像辅助数据误差，将其引起的SAR图像方位和距离向反定位误差定义为Δnai_image和Δnri_image。目前，星载InSAR系统主要包括单星重复航过InSAR和双星编队单航过InSAR，下面将针对这2种体制进行性能分析。

3.1 单星重复航过InSAR

单星重复航过InSAR系统中，主辅SAR图像辅助数据误差相对独立，而由目标位置误差引起的主辅SAR图像反定位误差可在一定程度上对消。因此，雷达几何图像配准法在单星重复航过InSAR数据处理中的方位和距离向配准误差可表示为

(32)

式中:Δna_target为目标位置误差在方位向分量;Δnr_regis为目标位置误差在距离向分量。

TerraSAR-X L1b图像产品辅助参数精度见表2。需要说明的是，TerraSAR-X系统斜距测量误差与观测场景的高程变化有关，难以定量描述，这里只能分析SAR图像辅助参数误差引起的方位向反定位误差。仿真结果表明：辅助参数引起的方位偏移量方差约为0.45 m(对应的σΔna1_image约为0.22像素)，这与TerraSAR-X系统几何校正试验结果(0.483 m)相吻合[10]。

由前可知，高程误差引起的距离向反定位误差主要随雷达平地入射角变化，而主辅SAR之间的垂直有效基线决定了主辅雷达平地入射角差异。因此，高程误差引起的主辅SAR图像配准偏移量误差可表示为

表2 TerraSAR-X L1b图像产品几何精度Tab.2 L1b image product geometric accuracy of TerraSAR-X

(33)

式中：θi,1和θi,2分别为主辅SAR平地入射角；B⊥为垂直有效基线；R为雷达斜距；Rsample为距离向采样间隔。

高程误差分别为15 m(SRTM DEM精度)和160 m(GTOPO30 DEM精度)时，雷达几何配准法图像配准偏移量随雷达下视角和垂直有效基线长度变化曲线如图5所示。由图可知，当垂直有效基线长度为1 000 m时，15 m高程误差引起的配准偏移量误差仅为0.01像素。由前可知，该误差远小于SAR图像几何参数引起的配准偏移量误差，而160 m高程误差引起的配准偏移量将达到0.1像素，量级与图像几何参数误差影响相当。

图5 雷达几何图像配准法配准偏移量误差Fig.5 Offset error of radar geometric image coregistration method

综上可知，重复航过InSAR雷达几何图像配准法精度主要受主辅SAR图像辅助参数精度影响，SRTM粗DEM高程误差引起的图像配准偏移量估计误差基本可忽略不计。对于实际的InSAR处理器，可采用SRTM DEM作为辅助高程信息，进行雷达几何法图像配准，之后采用基于数据的图像配准方法，降低SAR图像几何参数误差带来的影响，进一步提高图像配准精度。

3.2 单航过InSAR

目前，以德国TanDEM-X为代表的分布式卫星单航过InSAR系统得到了广泛关注[11]。相比于重复航过InSAR系统，分布式卫星InSAR系统由主星发射雷达信号，主辅雷达同时接收地面回波，此时主辅雷达面临的大气延迟基本相同。此外，由于基线测量精度较高，使得轨道测量误差对SAR图像配准误差的影响可忽略不计。

分布式卫星InSAR系统在获取干涉数据时通常工作于双基模式，此时主辅雷达面临时间同步和相位同步问题。时间同步直接影响辅图像距离向时间精度，而相位同步误差将导致SAR图像方位偏移等问题，影响辅图像的雷达几何精度。TanDEM-X系统在轨运行调试阶段的时间同步误差约为0.13 ns，其引起的距离向配准偏移量误差仅为0.01像素，而TanDEM-X的相位同步精度可达1°，其引起的方位偏移量将小于0.005像素。高程误差引起的主辅SAR图像配准偏移量误差可表示为

(34)

其大小约为重复航过InSAR的一半，这是因为单次航过垂直有效基线可等效为重复航过InSAR的二分之一。

综上分析可知，分布式卫星InSAR系统在利用雷达几何法进行图像配准时，主要受到相位同步误差、时间同步误差和粗DEM高程误差的影响。对于单航过InSAR系统，其图像配准处理流程应根据系统相位同步和时间同步精度决定。

4 结束语

本文对利用主辅SAR图像雷达几何进行InSAR图像配准的方法进行了研究。通过分析SAR图像反定位精度，研究了雷达几何误差和外部粗DEM误差对雷达几何法图像配准性能的影响。理论分析和仿真试验结果表明：

1) 粗DEM高程精度对配准精度的影响与垂直有效基线长度和雷达下视角有关。当垂直有效基线长度为1 000 m时，SRTM高程误差(15 m)引起的重复航过InSAR配准精度仅为0.01像素量级，单航过InSAR系统图像配准误差相应减半。

本文对星载InSAR处理器工程化设计和卫星系统指标设计具有重要的理论指导意义，可有效支撑我国未来星载InSAR技术的发展。