平面外夹角对X形圆钢管节点平面外抗弯承载力的影响

,,,,

(浙江工业大学 建筑工程学院,浙江 杭州 310023)

钢管截面构件对比开口截面构件具有优异的双向抗弯和抗扭性能优势,广泛地应用于土木工程和海洋工程结构[1-3]。其中相贯连接节点作为钢管结构中最常见的一种连接节点形式,支管直接焊接在主管表面而无加劲肋的构造特点,导致钢管相贯节点在很多情况下的承载效率低于1.0,即节点承载力低于构件(支管)的承载力。除了焊接球与螺栓球节点,钢管相贯连接节点也是单层网壳结构中常用的节点形式,其中X形圆钢管相贯节点因为几何形式简单而得到广泛应用[4-5],在竖向荷载、地震和风荷载等作用下,平面外弯矩成为单层网壳结构中的X形圆钢管相贯节点的主要内力。然而,目前国内外的相关规范[6-10]关于X形圆钢管相贯节点的平面外抗弯承载力计算公式是基于平面X形节点在支管轴力作用下的环模型理论[11],并结合试验研究结果发展而来,没有考虑支管与主管平面外夹角φ的影响,而空间结构中的支、主管在很多实际情况下往往存在一定的平面外夹角。

采用有限元法研究支主管平面外夹角φ对X形圆钢管相贯节点平面外抗弯承载力Mou的影响。通过有限元(经已有试验结果校验)分析计算获得关于Mou的大量数据,在对比有限元所得Mou和相应的HSE[9]规范计算值的基础上,提出在已有规范计算公式上乘以一个关于φ的系数(函数),用来考虑支主管平面外夹角对节点平面外抗弯承载力的影响,并通过参数分析和回归拟合最终获得函数的具体表达式。

1 节点有限元模型及其校验

1.1 X形圆钢管相贯节点的相关几何参数

单层网壳等空间结构中X形圆钢管相贯节点的主管两侧的两根支管往往尺寸相同,其几何构造及相关几何参数见图1,图中的θ,φ分别为支主管的平面内、外夹角,节点其他无量纲几何参数有支主管直径比β=d/D，主管径厚比γ=D/(2T)，支主管壁厚比τ=t/T。空间单层网壳结构中的X形圆钢管相贯节点,其两侧支管端部往往同时承受大小相同的向下(正向)挠曲的平面外弯矩Mo+,在地震或强风荷载作用下还可能产生向上(反向)的弯矩Mo-,如图1所示。

图1 X型圆钢管相贯节点的构造及加载简图Fig.1 Structure diagram and loading conditions of CHS X-joint

1.2 节点有限元模型及其校验

有限元法已经广泛应用于钢管节点的承载力、应力场分析等[12],其具有良好的精度,是一种实用的方法[13]。通常采用实体或壳单元模拟钢管节点性能,壳单元忽略了一些应力与应变分量,故在分析节点的局部应力及应变方面不如实体单元精准,但相对实体单元，壳单元具有计算耗时少等优点。Vander[14]验证壳单元可有效地模拟管节点,故采用ABAQUS中的壳单元S8R,节点中间核心区(中间3D的主管和根部d的支管)为近似正方形(边长为主管壁厚T)的单元,非核心区部分单元长、短边尺寸分别为3T,T。有限元模型中主、支管长度LD,ld分别取10D,4d,主管材料采用双线型强化模型,弹性模量E=206 GPa,屈服强度fy取某个钢材试验值283 MPa,强化阶段切线模量Et=E/100,采用Coupling(耦合约束)将支管端部截面的运动和其形心点(控制点)的运动约束在一起,再在控制点上施加转角(模拟集中弯矩作用),支管(视为杆件)假定为弹性(弹性模量同主管)。祝磊[15]的研究表明:对于支管荷载能自平衡的X形节点,主管两端边界条件影响小,笔者也尝试过分别采用固定支座和铰支座,所得的弯矩—转角曲线几乎重合,最终确定主管两端采用固定支座约束。

对承载力等节点性能的分析,往往跟节点的广义荷载—广义局部变形全程曲线有关,通过有限元计算获得节点的平面外弯矩Mo—转角ψ曲线,在此基础上通过采用类似变形准则[16]的方法来确定节点的平面外抗弯承载力Mou。其中,节点平面外弯矩Mo可通过读取控制点的反力获得,节点转角ψ的定义和获取方法可分直接法和间接法[17]两大类,这里采用直接法获得ψ,其表达式为

(1)

式中:δ1,δ2分别为壳单元S8R节点有限元模型中主管管壁的受拉、受压侧鞍点a1,a2(图1)沿着支管轴线方向的局部凸、凹变形量;d,t分别为支管截面直径、壁厚。

为了确保节点有限元模型能可靠地用于后续的参数化分析研究,通过已有节点试验结果b1-1和b3-1[18](具有支主管平面外夹角的两个试件)对有限元模型进行校验,节点b1-1,b3-1的几何参数对应为D=273,351 mm,β=0.9,0.7,γ=8.53,10.97,θ=89°,86°,φ=6.5°,12°,τ=0.75,0.75。需要说明的是,有限元中的单元类型与网格划分方式均同前文,为了完全模拟试验条件,主管边界条件改为同试验的铰接,支主管材料的弹性模量E与屈服强度fy则取材性试验结果;此外,节点的平面外弯矩Mo的定义从原文的Fld改为更合理的Fldn,其中F为支管加载端集中力、ldn为支管净长度(图1)。试验和有限元对比结果见图2,图2中test为试验结果,试验为受正向弯矩作用(工程中最常见的荷载工况),图2中的FEA+,FEA-分别为正、反向弯矩作用下的有限元结果。由图2可知:FEA+所得的弯矩—转角(Mo—ψ)曲线比FEA-所得曲线要高,即相同节点转角对应Mo+的值大于Mo-,且节点几何参数β越大则两条曲线的差异越大。可用如图3所示的模型进行定性解释,空间X形圆钢管相贯节点在平面外弯矩作用下的力学模型可简化为截面高度和宽度分别为T和Be(Be=ηD,η为一常数)、长轴和短轴分别为(D-T)/sinθ和(D-T)的二维椭圆环模型,椭圆环模型在Mo+作用时较长弧段A1B1受拉、较短弧段A2B2受压,Mo-作用时则相反,从结构稳定的角度看,较长弧段受压比受拉更不利,故节点在Mo+作用下所得的Mo—ψ曲线往往比Mo-作用下所得的曲线更高,支主管直径比β较大时弧段A1B1与A2B2之间的差异更大,正、反弯矩作用下所得Mo—ψ曲线的差异亦更大。由图2亦可知:FEA+总体上与试验结果吻合较好,故节点有限元模型中单元类型、网格划分方式完全可用于后续的有限元参数化分析。

图2 节点有限元所得弯矩—转角曲线与已有试验[18]的对比Fig.2 The comparison of load-displacement curves between FEA result and experimental results [18]

图3 正、负平面外弯矩作用下的节点受力分析模型Fig.3 Comparison between mechanical models under positive and negative out-of-plane bending moment

2 节点平面外抗弯承载力的判断准则

研究有限元分析支主管平面外夹角φ对节点平面外抗弯承载力Mou的影响时,首先要确定节点承载力的判定标准,变形准则[16]为钢管相贯节点承载力的常用判定标准,但变形准则主要用于节点的轴向承载力判断——即将节点局部变形达到0.03D时的荷载作为节点的轴向承载力。由图2可知:当节点转角约为0.07时,试验b1-1和b3-1达到承载力极值,依次约为246,166 kN·m,拟采用转角0.07 rad对应的弯矩值作为X形圆钢管相贯节点的平面外抗弯承载力Mou,b1-1和b3-1相应的值分别为242,164 kN·m,与试验所得承载力极限值很接近。此外,有限元分析亦表明,当节点转角达到0.07 rad时,节点的管壁局部凹(或凸)变形接近0.03D。

《钢管结构技术规程》[6]对各国的平面X形圆钢管相贯节点(φ=0°)的平面外抗弯承载力规范公式(钢材强度设计值f置换为钢材屈服值fy)与用来拟合公式的相关试验数据进行统计分析。分析结果表明:规范HSE公式[9]与试验结果最接近且离散度较小,规范ISO公式[10]偏小、但离散度更小,HSE和ISO的公式分别为

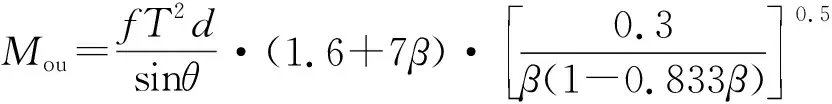
(2)

(3)

式中:f为主管钢材强度设计值,其余参数意义见图1。按HSE和ISO公式计算b1-1所得节点承载力(f置换为屈服强度fy)分别为195.5,163.5 kN·m,其与试验承载力的比值依次为0.81,0.67,式(2,3)计算b3-1所得承载力分别为138.4,120.8 kN·m,其与试验承载力的比值依次为0.84,0.74。可见,HSE公式与试验结果相对更接近,我国《钢管结构技术规程》[6]亦采用HSE的公式,在此基础上偏安全地乘以折减系数,并且乘以考虑主管轴力影响的参数Qf。

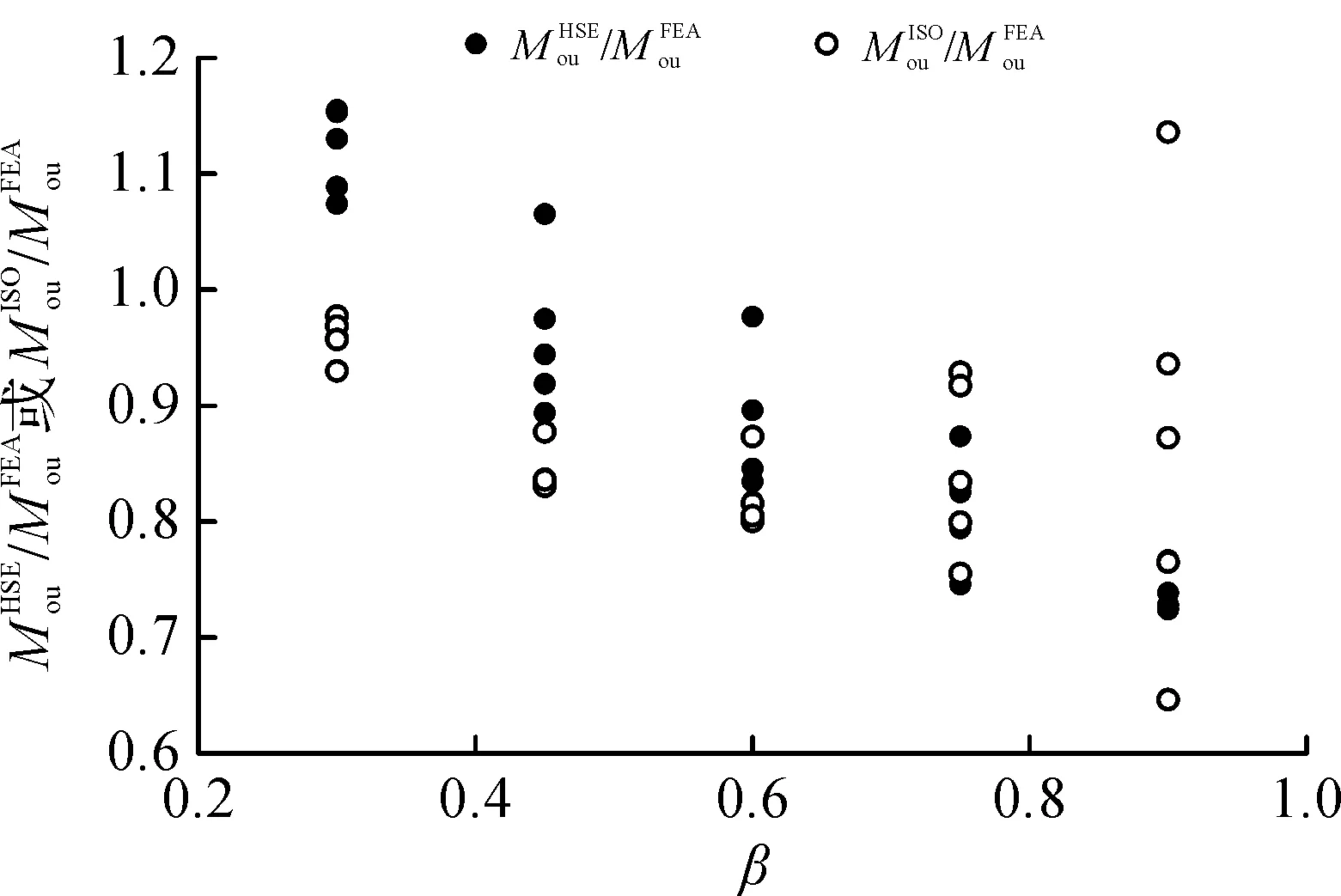
图4 有限元所得节点承载力与规范HSE和ISO的比较Fig.4 Comparison out-of-plane flexural capacity of the X-joints between FEA results and formulae of HSE and ISO code

3 面外角对节点承载力的影响

在前面平面外夹角φ为0°的25个节点有限元模型的基础上,保持其他节点参数不变,而增加φ=10°,20°,30°,45°的节点有限元模型(φ≠0°的每个节点均有正、反向弯矩作用)并计算得到节点抗弯承载力Mou,将φ≠0°的节点抗弯承载力与相应的φ=0°的值进行对比,用来分析支主管平面外夹角(面外角)φ对X形圆钢管相贯节点平面外抗弯承载力的影响,列于图5。图5中横、纵坐标分别为γ,Moun/Mou0，而Moun,Mou0分别为φ≠0°和φ=0°时的节点抗弯承载力,其中Moun又可进一步分为正、反向弯矩作用下的节点抗弯承载力Moun+,Moun-;图5中的“正”“负”分别表示Moun+,Moun-,如“β=0.3正”“β=0.3负”分别表示β=0.3的Moun+/Mou0,Moun-/Mou0。另外需要说明的是,搭接节点的受力性能与间隙节点差异较大,而为了避免φ和β同时较大而导致在支管根部出现搭接,故φ分别为20°，30°,45°时，β最大值依次为0.9,0.75,0.6。

由图5可知:几乎所有的Moun+/Mou0都大于1.0，而Moun-/Mou0几乎都小于1.0,且β越大则Moun+/Mou0及Moun-/Mou0与1.0的差异越大,说明β越大则φ对节点平面外抗弯承载力的影响越大,尤其是β和φ同时较大时,如β=0.9且φ=20°,第1节的环模型(图3)亦定性解释了这个特点。但仅γ变化时,Moun+/Mou0及Moun-/Mou0变化较小,说明γ对Moun+/Mou0及Moun-/Mou0的影响较小,可以忽略。

由图5亦可知:当β≤0.6时,φ对的节点承载力的影响较小;当β≥0.75时,φ对的节点承载力有一定程度的影响,可在已有规范公式基础上乘以一个关于β和φ的函数f(β,φ),用来反映φ对节点抗弯承载力的影响,且应满足φ=0°时f(β,φ)=1.0,即可退化为已有的规范计算公式。对β分别为0.75和0.9的50个比值数据(Moun+/Mou0,Moun-/Mou0各25个)进行分析和拟合尝试,结果表明:函数f(β,φ)分别取(1+aβbsinφ)和(1-aβbsinφ)时,能较好地反映比值Moun+/Mou0和Moun-/Mou0随着β与sinφ的变化规律,且函数形式较简单。通过回归拟合得到f(β,φ)的具体表达式为

图5 支主管平面外夹角对节点平面外抗弯承载力的影响Fig.5 Effect of out-of-plane angle (between chord and brace) on the out-of-plane flexural capacity of CHS X-joints

(4)

同时,给出β≥0.75时X形节点有限元所得比值Moun+/Mou0及Moun-/Mou0与式(4)计算值的相对误差,见图6。由图6可知:绝大部分误差上小于10%,最大误差约13%,说明式(4)较好地反映支主管平面外夹角φ对X形圆钢管相贯节点平面外抗弯承载力的影响。

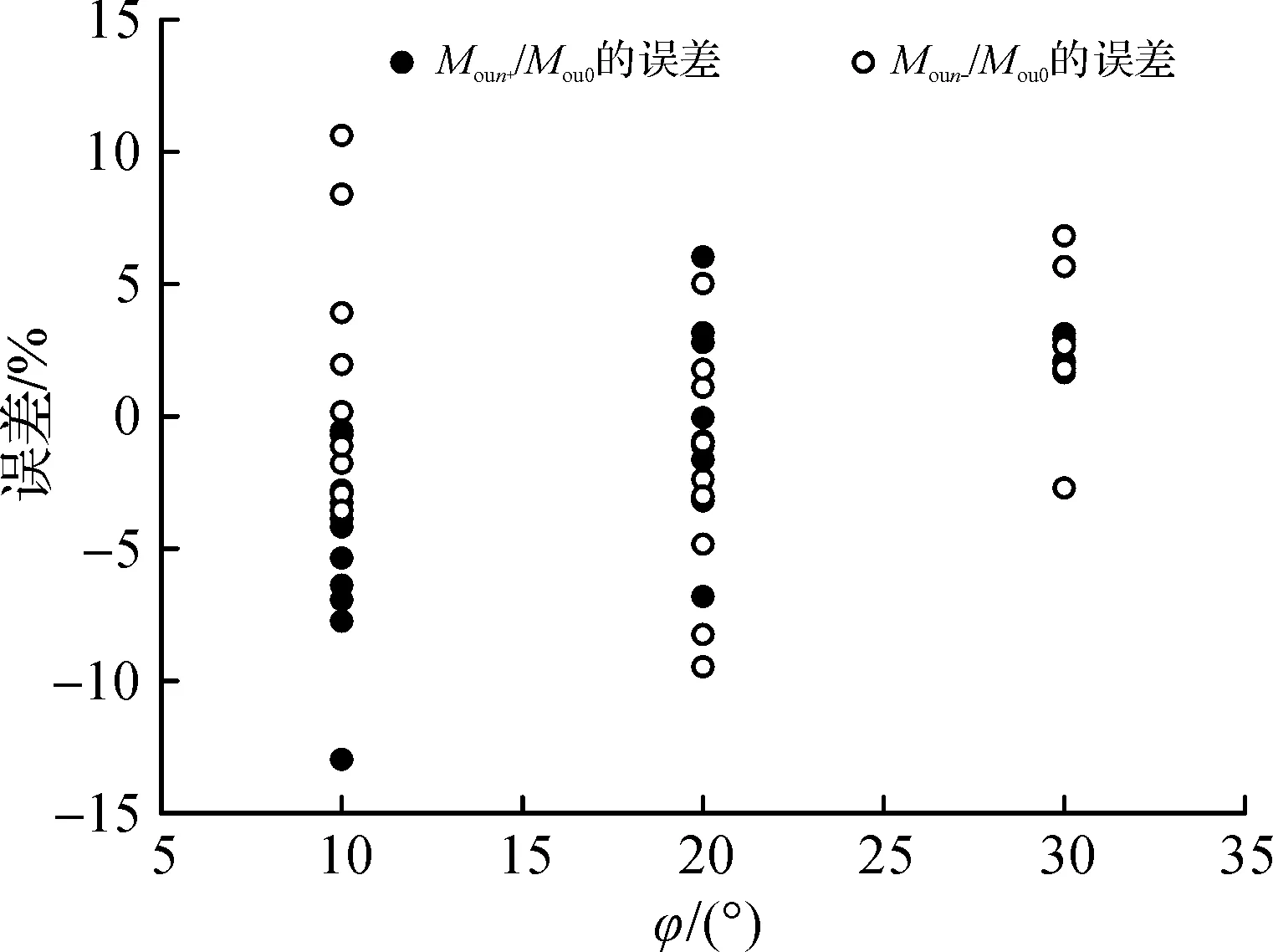
图6 式(4)与有限元所得值之间的相对误差Fig.6 Relative errors between FE results and Eq.(4)

根据上述分析结果,关于φ≠0°的空间X形圆钢管相贯节点的平面外抗弯承载力计算,可在已有规范[9-10]的基础上乘以一个关于β与φ的无量纲函数,具体应用如下:

1) 当β≥0.75时,无量纲函数即为式(4)。

2) 当β≤0.6时,当节点处于正向平面外弯矩作用(工程中最常见的荷载工况)时,忽略φ对节点抗弯承载力的有利作用,无量纲函数取1.0;当节点处于反向平面外弯矩作用时,无量纲函数取0.9,用来反映φ对负向平面外弯矩作用下节点承载力的不利影响。

3) 当0.6<β<0.75时,可在1),2)的基础上简单地取两者关于β的线性插值。

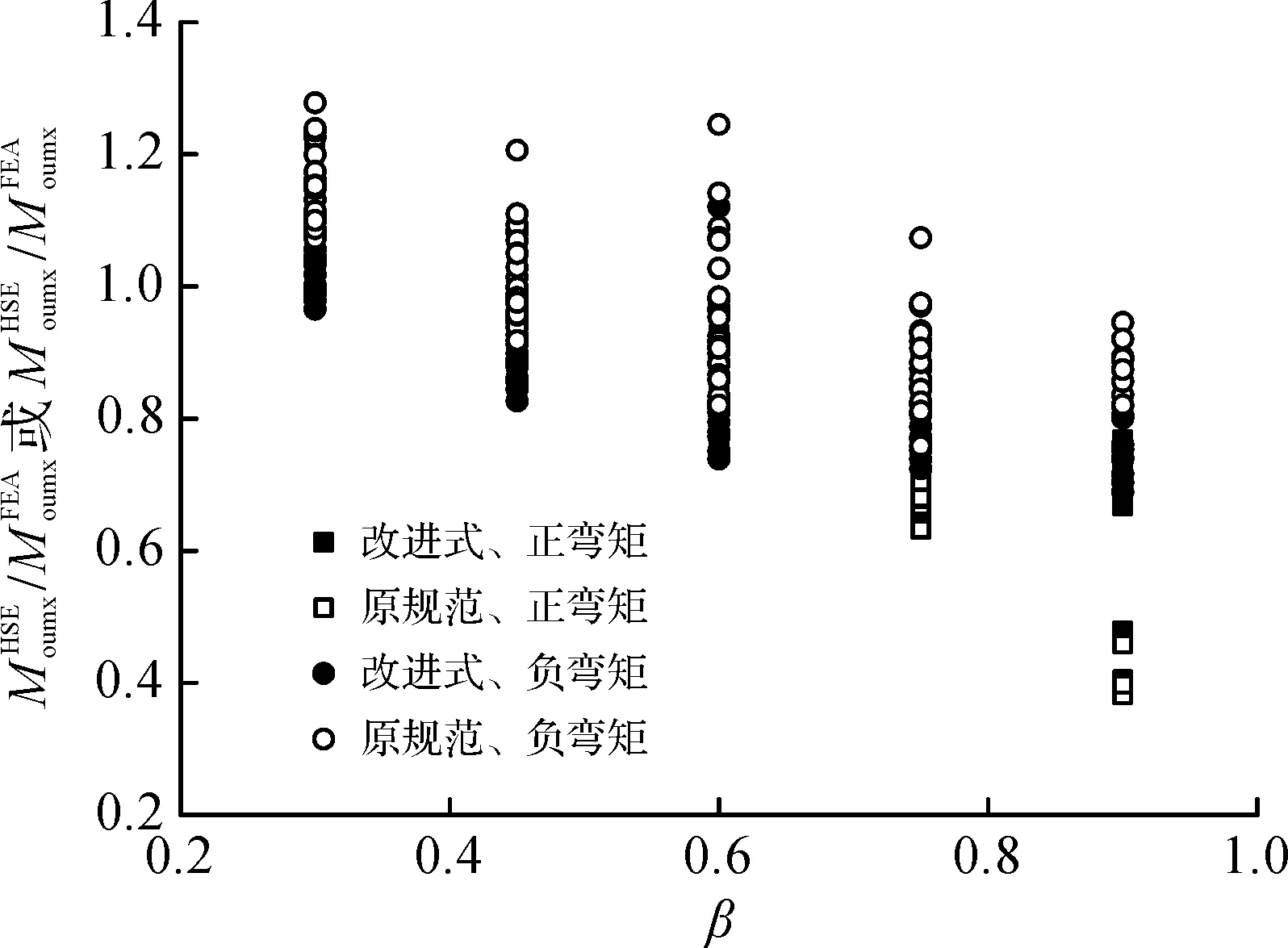
图7 改进计算式与HSE规范的比较(有限元结果为中介)Fig.7 Comparison between the results of the improved formula and HSE formula (results of FEA as intermediaries)

4 结 论

通过对比有限元计算结果和已有试验数据、规范计算公式,可将0.07节点转角作为X形圆钢管相贯节点平面外抗弯承载力的判断准则。面外角φ有利于空间X形圆钢管相贯节点的正向平面外抗弯,但不利于反向平面外抗弯。β≤0.6的节点的平面外抗弯承载力受φ的影响较小,此时可考虑忽略φ对节点正向抗弯承载力的增强作用,在已有规范公式基础上乘以折减系数0.9,用来考虑φ对节点反向抗弯承载力的不利影响;β≥0.75的节点抗弯承载力受面外角φ的影响较大,此时在已有规范公式基础上乘以一个无量纲函数f(β,φ),用来反映φ对节点抗弯承载力的影响。

本文得到浙江工业大学创新性实验项目(SYXM1719)的资助。