Narayana数相关恒等式的证明

修风光

(沈阳理工大学 理学院，沈阳 110159)

在xoy平面上沿整数格点按一定步伐行走的路径统称为格路。Dyck路是格路的一种，由于在有序分拆、无序分拆、恒等式的组合证明、RNA第二结构等研究中有广泛的应用，受到众多研究者的重视，对各种有限制条件的格路计数一直是组合数学中一个热门的研究课题。

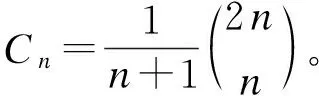
本文在对Dyck路的研究过程中得到了如下一个跟Narayana数有关的新的恒等式：

接下来给出此恒等式的证明及推广。

1 组合证明

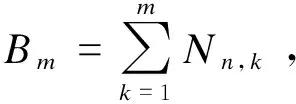
同时令D表示所有半长为n的Dyck路的集合，p(∂)表示一个半长为n的Dyck路∂中所含峰的个数。定义集合[1,n]和D的卷积[1,n]×D={(m,∂):m∈[1,n],∂∈D}。

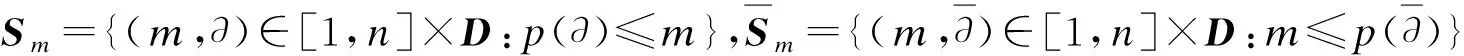
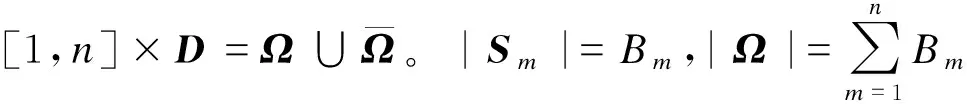
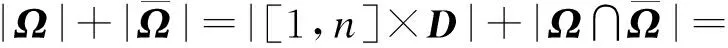
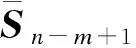
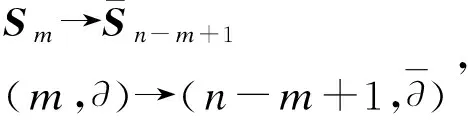
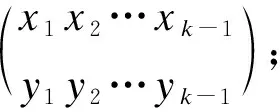
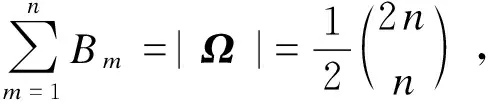
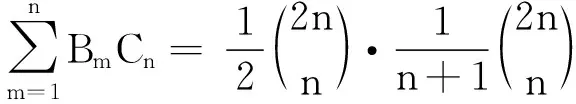
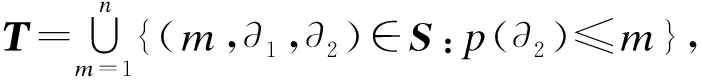
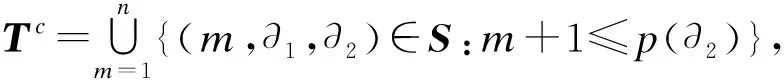
又因为|S|=|Τ|+|Τc|,

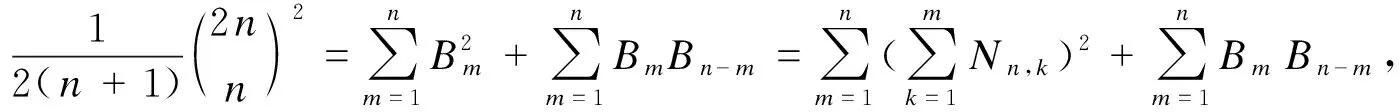
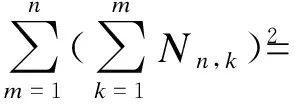
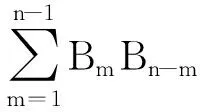
2 与Narayana数相关的发生函数

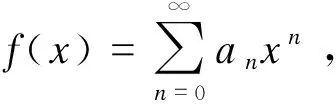
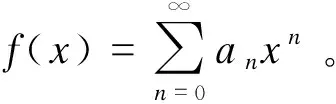
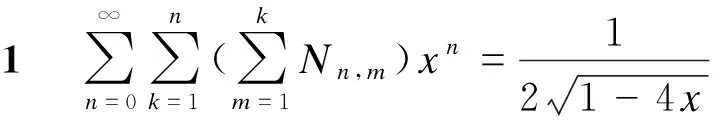
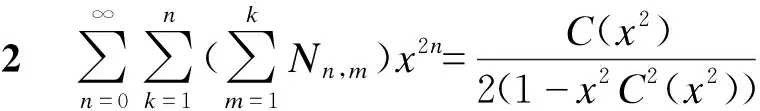
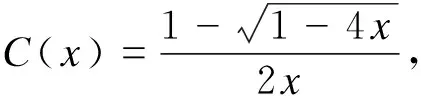
进而有

3 结束语

本文以Dyck路中特殊的点(如峰点或谷点)的坐标，运用数论知识，通过建立两个集合之间的双射，给出了与Narayana数有关的恒等式的组合证明及推广。同时还得到了一些与 Narayana数有关的发生函数。