小波各向异性模型肺部CT图像去噪

石振刚，李芹子

(1.沈阳理工大学 信息科学与工程学院,沈阳 110159；2.辽宁省人民医院 呼吸内科,沈阳 110016)

肺部CT图像是呼吸内科医生对呼吸系统疾病进行治疗的重要依据。但肺CT图像在获取、传输及存储的过程中不可避免地要受到各种噪声的干扰，从而会给病灶图像分割及医生判断病人病情带来不良的干扰，所以有关肺部CT图像的去噪问题显得尤为重要。

图像去噪是图像处理与识别过程中的第一个步骤，图像去噪的成败对后续处理与识别的效果起着至关重要的作用[1-3]。近年来，研究人员根据不同图像噪声的特征提出许多去噪算法[4-6]，但在去噪的同时较好地保持图像的边缘、纹理等细节信息这一问题并未得到很好地解决。基于小波分析的图像去噪方法由于能够同时进行时域及频域的局部信息分析，并且可以提取图像的局部奇异特征，因而可在去噪的同时保留图像中的高频信息，但其缺点是会出现伪吉布斯效应进而出现边缘信息模糊的现象[7-9]。基于各向异性模型的去噪方法主要是对整体图像进行去噪，去噪结果对去除噪声和保持边界有很好的兼顾，其缺点在于去噪过程中会平滑图像中的纹理信息[10-12]。所以，本文提出结合小波去噪和各向异性模型去噪优点的小波各向异性模型肺部CT图像去噪算法。

1 小波去噪

多尺度分析是小波变换的主要特点，可在频率域将图像分解为低频部分和高频部分。在低频部分，分解的小波系数数目较少但幅值较大，主要对应图像的有用信息。高频部分所对应的小波系数数目较多但幅值相对较小，主要对应于图像的噪声信息。图像小波去噪就是判断分解后小波系数幅值的大小，设定一个合理的阈值对小波系数进行判断从而达到去除图像噪声的目的。

图像小波去噪首先要根据去噪图像的特点选择合适的小波基函数。针对肺部CT图像的特点选择Daubechies小波(dbN)。dbN小波具有紧支集的标准正交基，其离散形式如下：

(1)

式中：m0表示小波函数；ω表示角向量；hk1是有限长度实数数列；k1=0,1,…,2N-1，为调整系数；N是小波阶数；e-iωk1是小波基。

(2)

式中：P表示小波的尺度函数；y表示小波的尺度基；k2=0,1,…,2N-1，为调整系数，是有限长度实数数列；C是多项式表达式。

设dbN的小波系数为u，去噪的阈值T采用式(3)获得。

(3)

式中：t′为crit(t)最小值时的解；c(k)是小波包系数；σ为噪声的标准差；n为系数的个数；α为调整参数。

阈值函数为式(4)。

(4)

式中，sign()表示符号函数；un为去噪后的小波系数。

如此可得到小波去噪后的小波系数，然后经小波反变换，即可得到空间域的去噪图像。

2 各向异性模型去噪

各向异性扩散模型是国外学者Perona和Malik根据热传导方程建立的[13]。其去噪的基本思想是在尺度区域内对图像进行去噪，而在边缘区域减少不必要的平滑。在用各向异性扩散模型进行图像去噪时通过采取梯度微分算子对图像的边缘进行检测，因而这种去噪算法很好地将图像去噪与图像边缘检测统一到各向异性模型中。通过数学分析，各向异性模型在本质上就是变化的热扩散偏微分方程：

(5)

在各向异性模型中，扩散系数的选择至关重要，若选择扩散系数为一个常数，那么各向异性模型就相当于一个线性低通滤波器。在图像去噪的各向异性模型扩散系数的选择上，sp(•)是梯度的函数，图像中的尺度区域梯度值较低，故在该区域的平滑效果应该较强。在图像中的边缘区域，梯度值较高，在该区域的平滑效果应该较弱。因而，图像去噪的各向异性模型扩散系数选择如下。

(6)

式中，lm(x,y,t)表示图像函数；k为阈值参数。

3 小波各向异性模型肺部CT图像去噪

小波去噪由于可在小波域对图像信号进行局部分析及奇异特征的提取，故可在去除噪声的同时保留图像中的高频信号，但存在边缘模糊及出现伪吉布斯效应。各向异性模型去噪的特点是在去除噪声的同时可以很好地保持图像的边缘信息，但存在图像中的纹理等高频信息也被平滑。因而将小波去噪与各向异性模型去噪融合，针对肺部CT图像，提出小波各向异性模型肺部CT图像去噪算法。算法首先对肺部CT含噪图像进行小波分解，然后在小波域进行小波阈值去噪，再进行各向异性模型去噪，最后得到去噪后的肺部CT图像。算法具体步骤如下。

步骤1 对原始含噪肺部CT图像进行小波变换，应用小波阈值方法进行去噪，判断去噪后峰值信噪比(PSNR)值，进行迭代处理，使PSNR值达到最大，得到相应的分解层数。根据得到的分解层数对原始图像进行小波分解及阈值去噪，然后进行小波反变换。

步骤2 针对步骤1处理后的图像进行各向异性模型去噪和迭代处理，使PSNR值达到最大，获得相应的阈值参数。根据得到的阈值参数进行各向异性模型去噪。

步骤3 输出去噪后的肺部CT图像。

4 实验结果及分析

本文对含噪肺部CT图像进行去噪实验，并与维纳滤波、中值滤波、小波阈值去噪算法及各向异性模型去噪算法进行比较，实验结果见图1。从去噪效果上可以看出：图1b中的维纳滤波(7×7)及图1c中的中值滤波(7×7)在去噪时造成了整体图像模糊，图1d中的小波阈值算法虽然可以很好地保护图像的纹理细节但边缘信息较模糊，图1e中的各向异性模型去噪算法虽然能够去除加噪图像的一部分噪声，但由于其去噪原理简单，对于有用信号和噪声信号的区分不细致，导致在去除部分噪声的同时也模糊了部分有用信号。图1f中的本文算法由于充分利用了小波阈值去噪算法和各向异性模型去噪算法的优点，使得去噪后的肺部CT图像细节、纹理等有用信号较清晰，在去噪的同时强化了图像的纹理和边缘信息。

图1 算法比较的含噪肺部CT图像去噪

本文还对四位病人的含噪肺部CT256×256图像(图2所示)进行了算法对比实验，测试PSNR值及结构相似性(structural similarity image measurement，SSIM)之间的对比，PSNR的定义如下。

(7)

式中：I(i,j)为(i,j)点的原始图像灰度值；Y(i,j)为(i,j)点的恢复图像灰度值；MN为图像的像素个数。

结构相似性SSIM是衡量两幅图像相似度的指标，其取值区间为[0,1]，该指标分别从亮度、对比度、结构三方面度量图像的相似性。SSIM定义如下：

(8)

式中：μX和μY分别表示图像X和Y的均值；σX和σY分别表示X和Y的方差；σXY表示X和Y的协方差；C1和C2为常数。

测试结果列于表1～表4。从表中可以明显看出，所提算法的PSNR值都高于维纳滤波去噪算法、中值滤波去噪算法、小波阈值去噪算法及各向异性模型去噪算法的PSNR值。

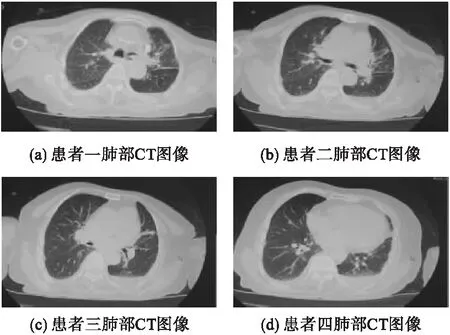
图2 四位患者的含噪肺部CT图像

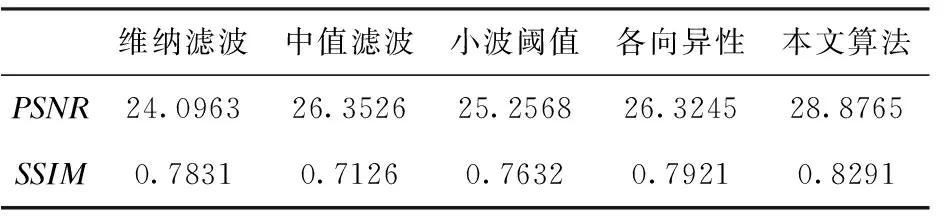
维纳滤波中值滤波小波阈值各向异性本文算法PSNR24.096326.352625.256826.324528.8765SSIM0.78310.71260.76320.79210.8291

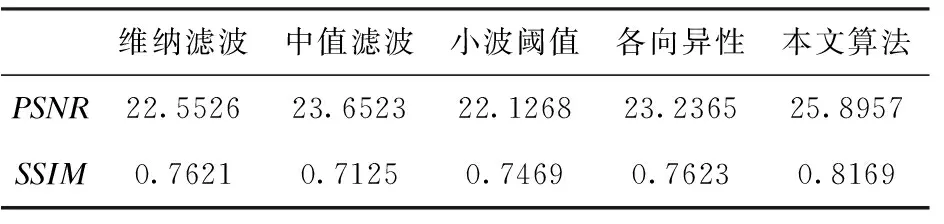
表2 不同去噪算法时的PSNR值和SSIM值(患者二)

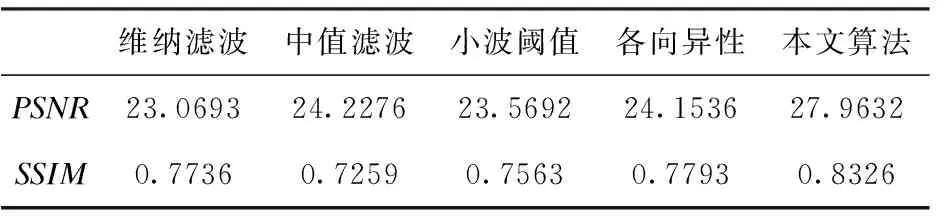
表3 不同去噪算法时的PSNR值和SSIM值(患者三)

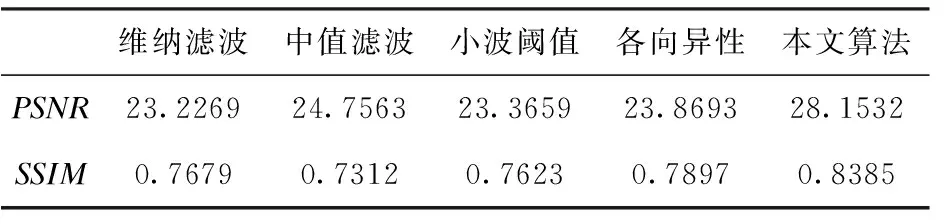
表4 不同去噪算法时的PSNR值和SSIM值(患者四)

5 结束语

为滤除肺部CT图像中的噪声并很好地保持图像中的边缘、纹理等细节信息，将小波去噪与各向异性模型去噪的优点融合，提出一种小波各向异性模型肺部CT图像去噪方法。实验结果表明所提方法具有较高PSNR值和SSIM值，并且能较好地保持肺部CT图像的边缘、纹理等细节信息。证实了本文算法针对肺部含噪CT图像去噪的有效性。