基于灰色理论的自动步枪故障预测

薛洪彬,张 健,杨 丽,2,郭 创

(1.沈阳理工大学 装备工程学院,沈阳 110159;2.重庆建设工业(集团)有限责任公司,重庆 401300)

就目前我国枪械的性能来说,其总体性能与国外同类产品相比确实具有一定差距。我国某型号步枪的综合性能相当于美国的M16A2、俄罗斯的AK74M。该步枪的机械系统复杂,各种原因引起的故障问题不可避免。由于步枪多为单人手提武器,伴随士兵行动,使用时多为贴身操作,一旦发生故障,即有危害人身安全的可能[1-3],因此步枪故障问题的研究具有十分重要的意义。

关于步枪典型故障分析的研究一直没有间断过。余家武应用故障分析中的FMECA和FTA两种方法对某自动步枪的主要故障进行了分析[4];宫鹏涵等通过ADAMS建模软件建立了某自动步枪射击时的动态特性[5];蔡伟等将故障树和模糊理论相结合对某自动步枪的卡弹故障进行了很好的分析[6];都业宏等将云模型理论和语言方式规则语言应用于预测兵器试验故障,对兵器试验的故障预测问题进行了相关的研究[7];Jia Z H等通过动力学仿真也对某步枪的相关问题件进行了研究[8]。

本文主要是应用灰色系统理论对某自动步枪的故障进行预测分析。灰色系统理论是由邓聚龙教授于1982创立的,在各个领域中已得到广泛的应用,并取得了的较好的成果。灰色系统理论是一种研究某些既含有已知信息又含有未知信息或者未确知信息的系统理论和方法。从杂乱无章的、有限的、离散的数据中找出数据规律,然后建立相应的灰色模型进行预测,灰色理论的实质是对原始随机数列采用生成信息的处理方法来弱化其随机性,使原始数据序列转化为易于建模的新序列[9-10]。自动步枪在使用过程中受多种因素的影响以及自身故障的累积效应,使步枪的使用与产生故障之间有了很重的灰色关系[11]。故障的形成和发展所包含的模糊性和随机性使得常规的分析方法在故障预测中无法得到准确的结果,因此采用适合处理模糊关系的灰色系统理论。

基于以上问题,本文提出了一种建立在GM(1,1)模型基础上的自动步枪故障的灰色预测方法。

1 GM(1,1)模型

某自动步枪故障的灰色预测的基本方法是对采集的数据信息的时间序列进行适当的处理,按照微分方程拟合的方法建立灰色动态模型。自动步枪发生故障和故障的发展具有不确定性,而把具有不确定性的系统称之为灰色系统,因此可以将自动步枪的故障问题视为灰色系统。将灰色理论应用于故障预测的基本原理是把被预测的系统看成一个灰色系统,由已知的信息去推测含有故障模式的未知信息的状态、特征以及发展趋势,同时预测未来故障的发展趋势并作出决策,即灰色系统的白化过程。灰色建模就是把无规律的原始数列经过处理使系统中各因素间的关系数量化、具体化,生成比较有规律的数列用以建立微分方程[12-13]。

以GM(1,1)预测模型为主的灰色系统预测方法因其所需建模数据少、计算简便和应用广泛而在预测领域中占有重要地位[14]。GM(1,1)预测模型的基本思路为:把一个随时间变化的数据序列通过累加,生成新的数据序列,根据灰微分方程的白化微分方程的解,还原后即得GM(1,1)预测模型[15]。

若采集的原始数据时间序列为:

X(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n))

式中,X(0)为非负序列；X(1)为X(0)的1-AGO序列。

X(1)=(x(1)(1),x(1)(2),x(1)(3),…,x(1)(n))

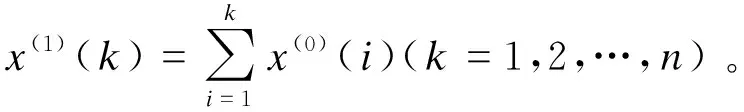
设Z(1)为X(1)的紧邻均值生成序列

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

式中

(1)

x(0)(k)+az(1)(k)=b

(2)

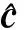
(3)

式中，

GM(1,1)模型的白化方程(也叫影子方程)为

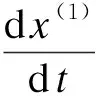
(4)

白化方程(4)的解也称时间响应函数，为

(5)

GM(1,1)模型的时间响应序列为

k=1,2,…,n

(6)

还原值为

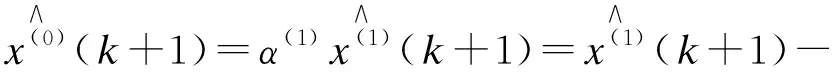
(7)

2 灰色预测实例

对某自动步枪15000发弹射击过程中出现的故障进行整理统计如表1所示。

表1 故障数据

将表1中的前五组数据作为原始数据建立预测模型,经计算得到参数a=-0.1985,b=7.4907

所以,可以得出其预测模型为

x(0)(k+1)=(1-e-0.1985)(x(0)(1)+37.7365)e0.1985k,k=1,2,…,n

经计算得到实际值、第一组预测值及误差分析结果，如表2所示。

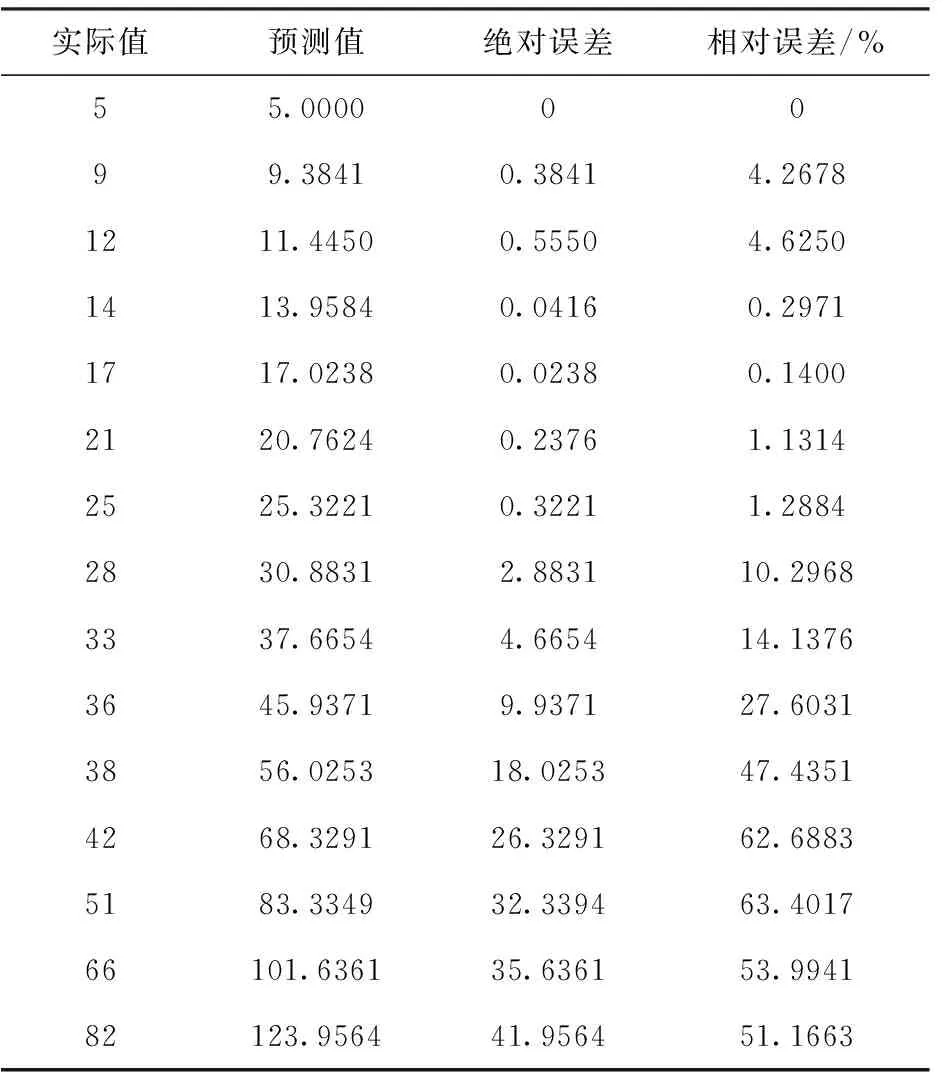
表2 实际值、第一组预测值及误差分析结果

实际值与灰色预测模型的第一组预测值的拟合曲线如图1所示。

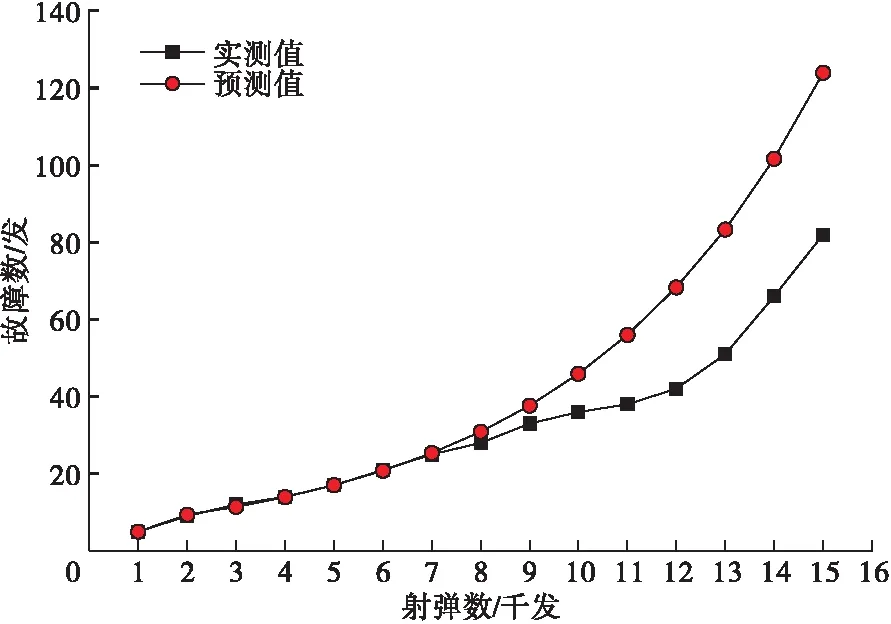
图1 实际值与第一组预测值拟合曲线

由表2及图1可知,前两组数据拟合程度较好,数据原点附近最小相对误差为1.1314%；后面几组拟合较差，其相对误差超过10%,而且距离原点数据越远误差越大,这也正符合灰色预测的特征,即:适用于短期预测,而长期预测误差较大。

将表1中的前十组数据作为原始数据建立预测模型,计算得到参数a=-0.1581,b=9.0963。经计算实际值、第二组预测值及误差分析结果，如表3所示。

实际值与灰色预测模型的预测值的拟合曲线如图2所示。

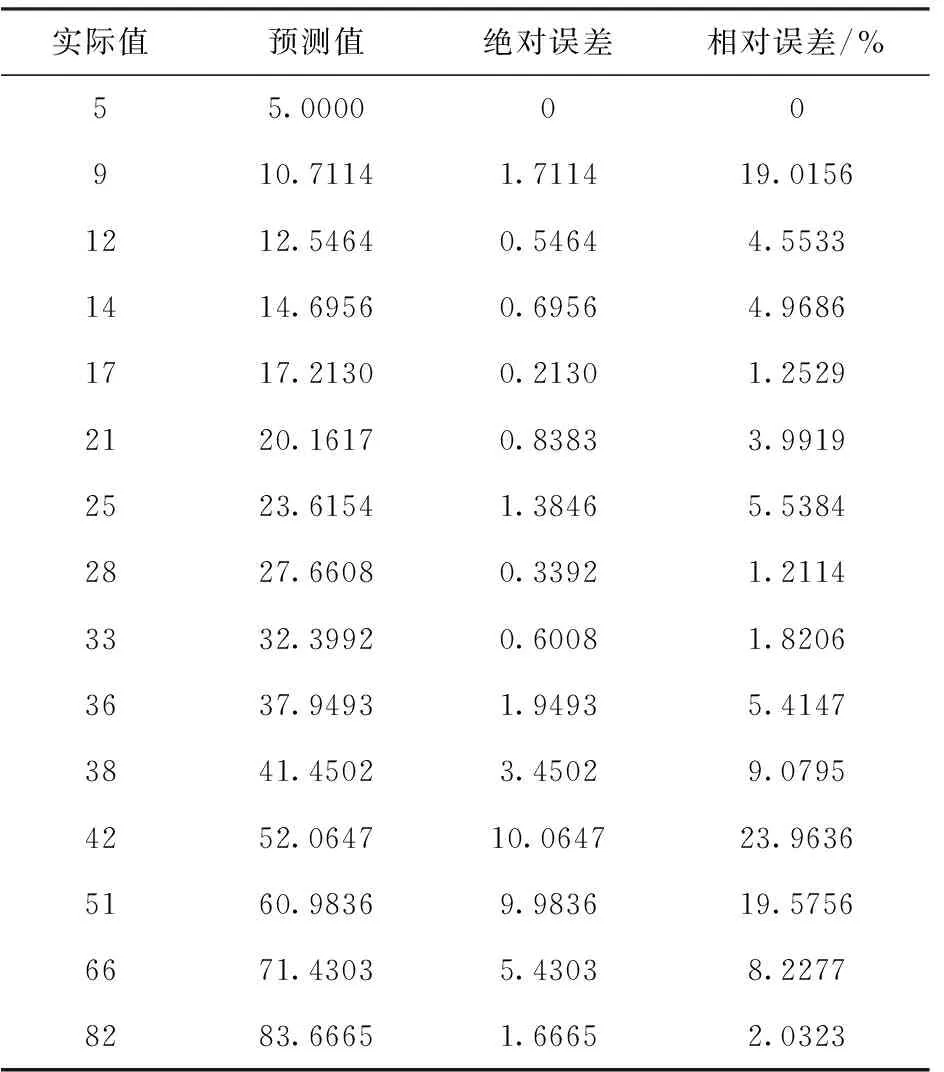
表3 实际值、第二组预测值及误差分析结果

由表3可知，在数据原点附近其最大相对误差为9.0795%，相对误差小于10%。

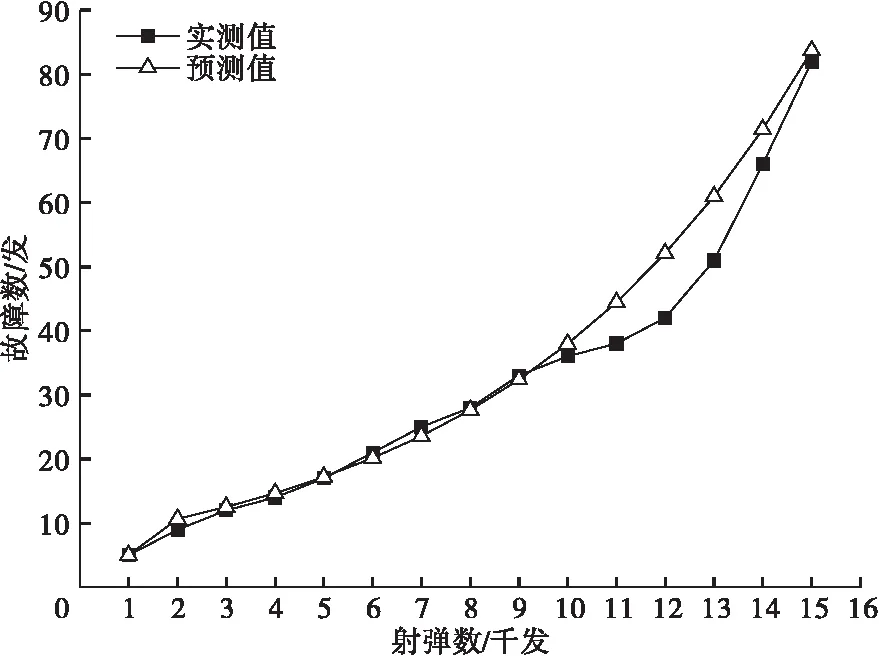
图2 实际值与第二组预测值拟合曲线

由图1和图2可以看出,随着新信息加入，模型的预测效果比旧信息的预测效果要好得多。这是因为随着枪械系统在使用过程中的发展,不断地有一些新的随机扰动因素进入到系统之中,使得系统的发展陆续的受到影响。同时旧的数据随着新信息的补充在系统中的影响也会逐渐减弱,尤其是随着系统变量的积累,整个系统也会发生变化,旧的信息并不能反映出此时系统的整体特征,因此在预测过程中需要不断的添加新的信息。事实上,由于诸多因素的影响,用GM(1,1)进行预测,精度较高的只是原点数据以后的1～2个数据。一般来说,越往未来发展,越是远离时间原点,该模型的预测意义就越弱。在实际应用中,必须不断地考虑进入系统的扰动因素,随时将新的数据加入其中,以建立新信息模型进行动态预测[6]。

3 结论

(1)利用GM(1,1)能够很好地预测某自动步枪的故障发展规律,灰色预测在步枪故障预测中的应用是可行的。

(2)通过实际算例计算得到在数据原点附近其最小相对误差为1.1314%,最大相对误差为9.0795%,相对误差均小于10%。

(3)通过两次预测结果对比发现，在原始数据中不断加入新的信息可以提高后续的预测精度。

(4)将灰色系统理论应用于步枪故障预测的方法,简单实用,预测能力及可靠性强,可以广泛地应用到工程领域中。