后抛式离心抛撒子弹弹道仿真与试验研究

王佳奇,焦志刚,黄维平，张筱媛

(1.沈阳理工大学 装备工程学院,沈阳 110159; 2.辽沈工业集团有限公司,沈阳 110045)

子母弹是以坦克、步兵战车、自行火炮等远距离集群为作战目标的新型常规武器装备,具有效费比高、火力覆盖面积大、通用性好等特点。关于子母弹的抛撒及子弹弹道,国内外进行了比较深入的研究。1997年Jubaraj Sahu对子母弹旋转分离方式进行了研究[1];1999年EDGE H L等对子弹不同攻角、处于母弹不同位置时的气动参数进行研究及流体力学仿真计算[2];陶如意等对子弹外弹道初始条件计算方法进行了探讨,建立了抛撒弹道模型[3];孙新利等研究了子母弹静态开舱试验,用高速摄像机等设备记录并观察轴心起爆条件下火药的爆燃状态[4];蔡兴会等对燃烧室内压强和推动子弹运动的压强之间进行了对比,提出了一种新的子弹的弹道计算方法[5];刘琨进行了子母弹子弹抛撒动力学分析,建立了某子母弹的干扰器子弹运动的外弹道模型[6]。子母弹子弹飞行特性、落点散布受多种因素影响,如抛撒时母弹的高度、弹道倾角、赋予子弹的初速、气动阻力、随机风等[7-8]。在确定了有规律的影响因素后,处理一些随机因素成为必要,起源于20世纪40年代中期的Monte Carlo方法[9-10]使处理这些随机因素成为可能。本文研究子弹弹道运动方程,并基于试验数据和蒙特卡洛法,应用Matlab对子弹的弹道及散布特性进行数据分析和仿真研究,根据仿真与试验结果着重分析抛撒高度对散布的影响。

1 子弹落点的影响因素分析及处理

子母弹采用后抛式开舱,当到达预定开舱高度时,时间引信作用引燃抛射药,推板在抛射压力作用下推动上子弹串、隔板、下子弹串运动,战斗部螺纹被剪切,完成开舱过程。抛撒方式为离心惯性抛撒。开舱后,在离心力作用下,支筒与最下层子弹抛出并分离,第二层子弹及第三层子弹陆续抛出,最后落地形成椭圆形散布。

子弹抛撒、飞行到落地的过程中受诸多因素的影响,进而影响子弹落点散布。所以在计算弹道时,加入干扰因素能使计算结果更符合实际,为此建立阻力系数和子弹落点随机模型。

(1)阻力系数模型:子弹的阻力系数取决于弹丸的速度、外形和姿态。各枚子弹的抛出速度差较小,对阻力系数影响不大;但抛出姿态不同,对阻力系数有一定影响。各子弹的阻力系数在一定范围内呈正态分布,该分布下的系数可表示为基本阻力系数与正态随机量之和,如式(1)所示。

(1)

式中:Cx、Cy、Cz是子弹各方向的阻力系数;Cx0、Cy0、Cz0是基于弹型、依据实际弹道数据和经验公式计算所得的子弹各方向的基本阻力系数;δx、δy、δz是呈正态分布的随机数;r1、r2为相互独立的均匀随机数(可利用斐波那契-同余法生成);θ是弹道倾角。

(2)子弹落点模型:时间引信控制子母弹开舱,其作用时间误差影响抛撒高度,试验数据显示母弹开舱高度在预期高度±5%范围内。子弹抛撒时处于下落段且高度较低,在此高度变化范围内,子弹姿态和速度变化较小,误差主要体现在抛撒高度上。将抛撒高度Y0在Y0±5%范围通过生成随机数的方法取10个随机高度,如式(2)所示。再通过仿真程序计算生成10组随机落点坐标后,对10组坐标取平均值得最终落点坐标,如式(3)、(4)所示。

yk=y0(1+rk)

(2)

(3)

(4)

式中:Yk是随机高度;X和Z分别是射程和方向散布;k是随机高度编号1～10;rk是-0.05至0.05之间符合均匀分布的10个随机数(由蒙特卡洛法生成)；n为随机数的个数。

2 抛撒过程数学模型

子弹外形为轴对称,且为近地抛撒,设弹轴速度与速度方向一致,由此可建立子弹三自由度质点弹道仿真模型,加入随机模型,对子弹从抛撒到着地的整个过程进行数值仿真。

2.1 坐标系建立和子弹初始位置分析

以开舱抛撒时第一层子弹排布中心在地面的投影为O点,母弹运行方向在地面投影为X轴正方向,O点指向抛撒位置为Y轴正方向,建立地面坐标系。则第一层子弹排布中心的坐标为(0,Y0,0),坐标系及子母弹装配方式如图1所示。

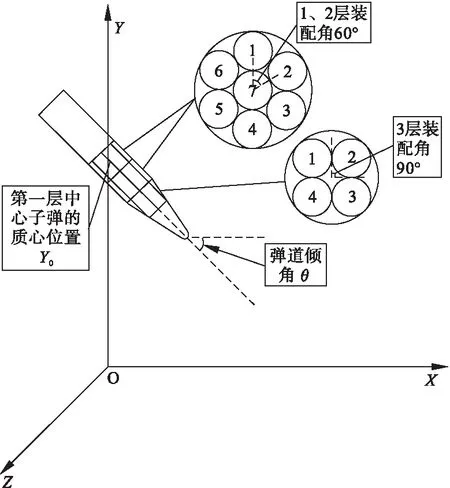
图1 子弹分布及位置图

根据子弹装配方式,各枚子弹在抛撒时的初始位置不同。抛撒高度为Y0时,各枚子弹初始位

置坐标如表1所示。

2.2 子弹速度的计算

母弹旋转产生的角速度,给予子弹切向分速度。在坐标系中,以第i层第j圈第k枚子弹为研究对象,该枚子弹的装配角为τ,其相对于母弹的切向速度的方向为τ+90°,弹道倾角为θ,则子弹各方向切向分速度的通用公式为式(5)。

(5)

式中:vτ是以子弹质心到弹轴的距离为半径、母弹转速为角速度,二者相乘得到的子弹切向速度;Δγ是由各层子弹抛撒时间偏差引起的邻层角度差。但第一层和第二层中心子弹各方向切向速度为0。

表1 子弹初始位置表

表中：d是子弹的直径；L是子弹的全长；γ是由于子弹抛撒顺序不同引起的邻层角度差；h是由于子弹抛撒顺序不同引起的邻层高度差。

将子弹切向速度分量与子弹轴向抛撒的速度分量进行合成,可得到抛出的三层18枚子弹在x、y、z轴上的速度分量的值。

(6)

式中,vm是抛撒时母弹的速度；vp是子弹反抛速度。

2.3 子弹质点弹道方程

子弹从舱内被抛出后,各层速度大小不同,各枚速度方向不同,从而形成一定的散布,根据子弹出舱后的受力情况,建立其质心运动模型。

(7)

式中:vx、vy、vz是子弹速度在地面坐标系上的分量;x、y、z是子弹质心坐标;ρ是空气密度;Sx、Sy、Sz是子弹在三个方向的迎风截面积;Cx、Cy、Cz是阻力系数;m是子弹质量;g是重力加速度;t是时间。

由式(5)、式(6)和表1中计算的子弹质点在坐标轴中的位置和子弹的分速度,带入弹道方程(7),解微分方程可得各枚子弹弹道。

3 子弹弹道仿真

根据子弹的弹道模型,利用Matlab软件编制子弹飞行弹道仿真程序,该程序在给出抛射点的母弹速度、抛射高度、抛撒时间、弹道倾角的条件下,应用四阶龙格库塔法可解得子弹弹道;进而通过画图程序生成落点分布、各枚子弹在三个坐标的变化以及分速度的变化坐标图。图2为计算子弹弹道仿真流程图。

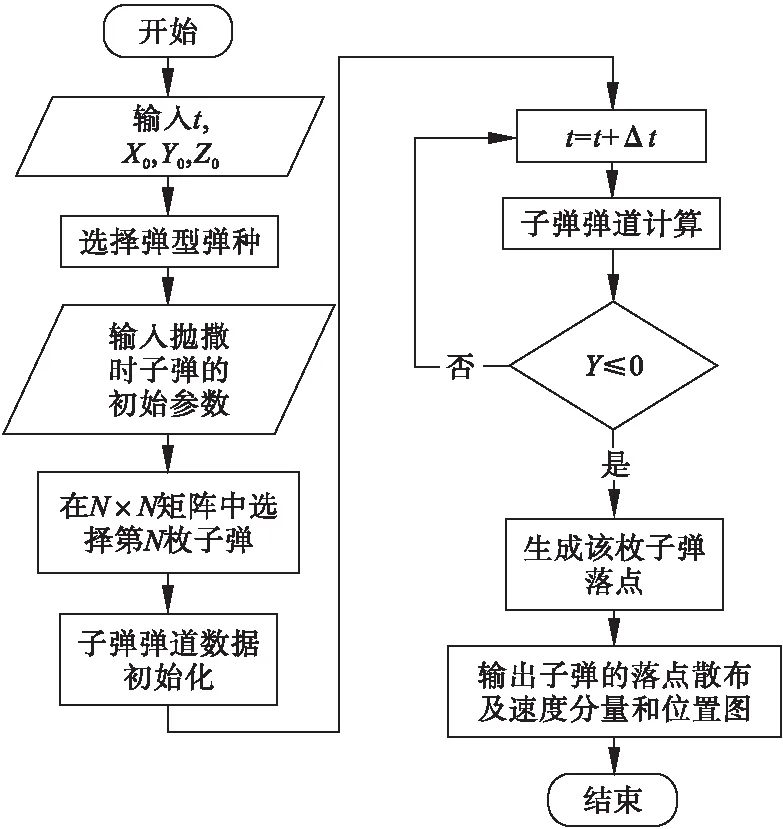
图2 程序流程图

4 子弹散布仿真与试验结果对比

根据子弹弹道仿真,将子弹落点数据写入Matlab画图程序,得子弹散布图;对不同抛射高度进行仿真,可得抛射高度对散布范围的影响;再将实测与试验数据对比,验证仿真正确性。

4.1 不同高度子弹散布规律

通过仿真程序,以开舱高度600m为起点,100m为间隔,计算到开舱高度为1500m时,子弹散布范围变化,见表2。

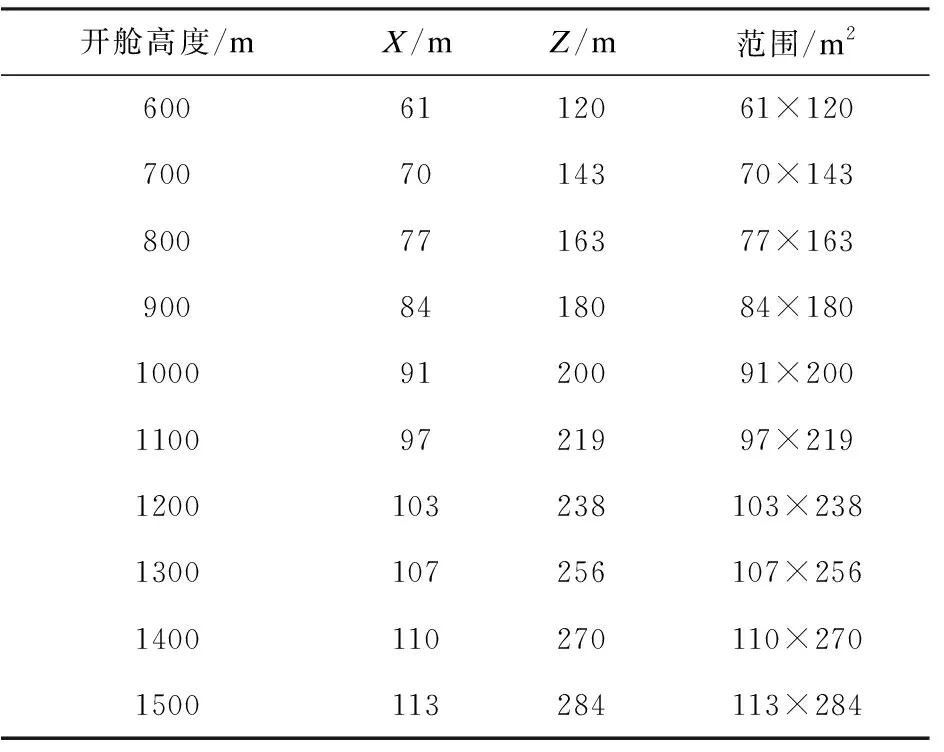
表2 不同开舱高度下子弹散布数据

从表2可以看出,随着开舱高度的增加,子弹散布范围增大,但范围增大量不断减小。实际上开舱高度增大到一定程度后,子弹散布范围不再增大;理论上存在一个最大开舱高度,子弹散布范围最大。

4.2 动态抛撒试验数据与计算结果对比分析

为验证仿真计算的正确性,从动态抛撒试验中,选取3发子母弹的数据进行对比分析,其实测抛撒高度分别为490m、630m、950m,做出其落点坐标图。将这三发弹的弹道数据带入程序进行计算,利用Matlab画图得到对应的仿真计算分布散点图,如图3～图5所示。

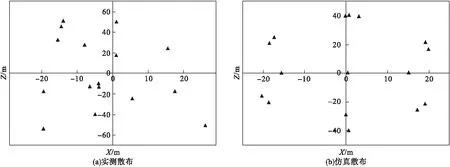
图3 490m抛撒高度下子弹实测与仿真散布对比

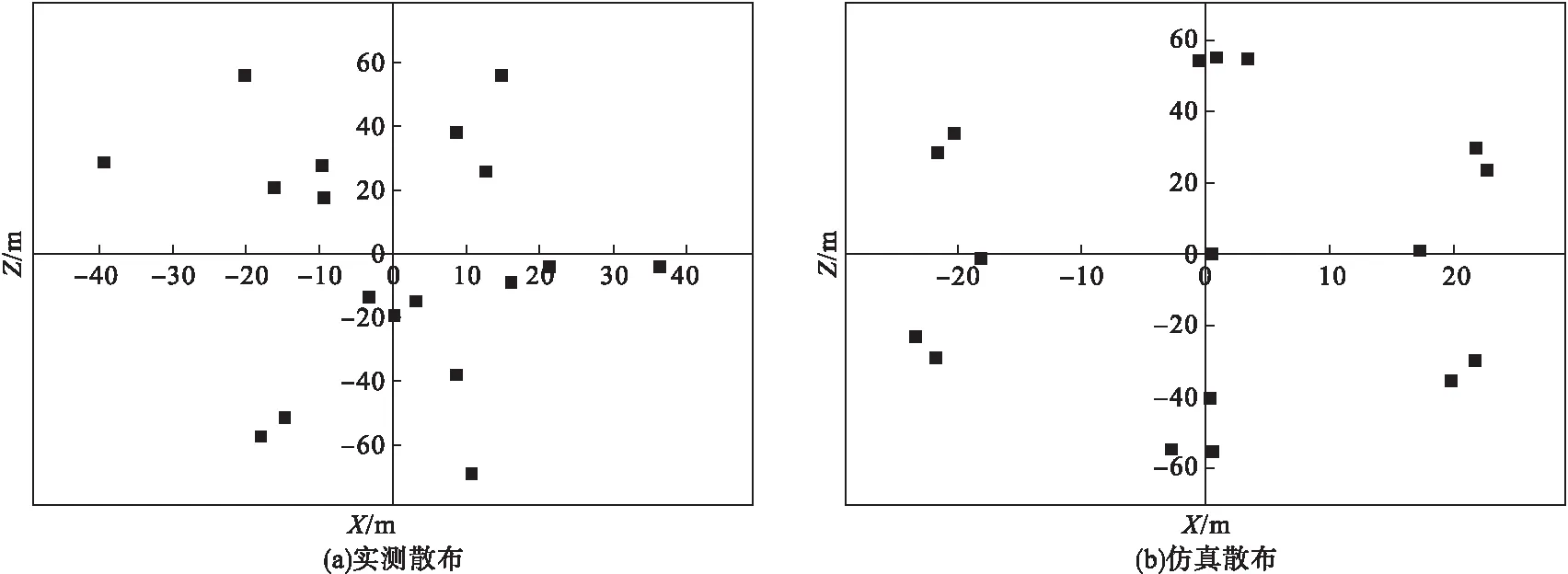
图4 630m抛撒高度下子弹实测与仿真散布对比

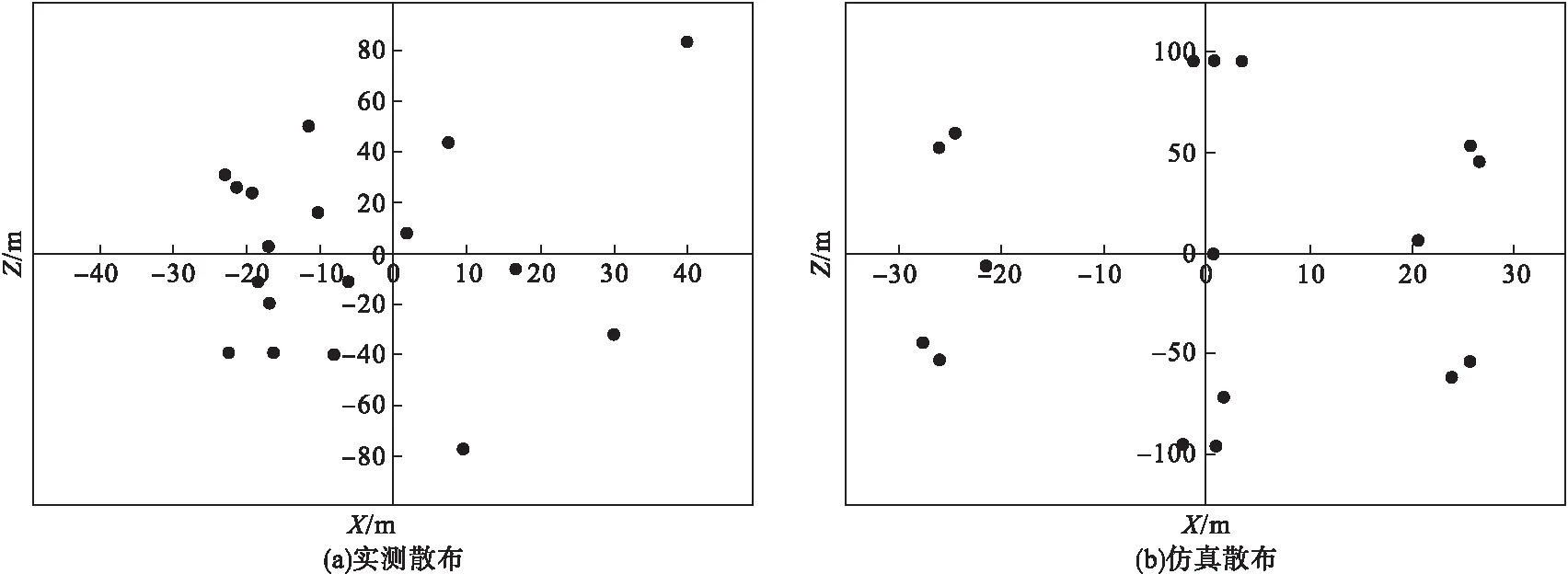
图5 950m抛撒高度下子弹实测与仿真散布对比

从试验结果可知,开舱高度为490m、630m、950m时,子弹散布范围分别为45m×102m、76m×127m、67m×157m,子弹散布范围随开舱高度的增加而增大。这是由于开舱高度增加后,子弹在空中运动时间增长,从而造成单枚子弹最远飞散距离加大,最终散布范围变大。再与仿真结果对比,仿真计算的范围分别为43m×80m,63m×115m,80m×155m,在范围的大小和随抛撒高度变化的趋势上,仿真与试验结果符合,证明仿真合理。散布范围加大后,虽然理论上可以在更远距离上打击目标,但子弹分布密度变小,无法保证可靠命中目标。因此,为保证一定范围内的子弹分布密度,提高命中概率,开舱高度需控制在合理范围内。

5 结论

本文将后抛式离心抛撒子弹弹道和落点散布分析结合在一起,研究某型号子母弹子弹抛撒过程的弹道理论和计算方法。

(1)计算出子弹在母弹中的位置及母弹旋转对各枚子弹的初始抛射速度,用蒙特卡洛方法处理阻力系数后建立子弹外弹道计算模型,经对490m、630m、950m抛射高度实测和仿真散布进行对比,说明该方法建立的模型合理;

(2)进行600m～1500m抛射高度的仿真,得到子弹散布变化规律,随着开舱高度的增加,子弹散布范围增大,但范围增大量不断减小。