基于投影轮廓的纸箱尺寸单目测量

刘 昶,王玉晗,张 鑫,刘丽萍

(沈阳理工大学 信息科学与工程学院,沈阳 110159)

长方体纸箱是一种主要的包装制品,对于邮政、海关、仓储、物流及某些加工企业,为进行货物的自动分拣和体积估算,需要对传送线上的长方体纸箱的三维尺寸进行自动化测量。一般的测量方法是采用三组光幕进行测量,当前光幕的分辨率可达1mm,每组光幕用于测量一维尺寸,这种方法结构比较简单,但在测长宽时要求箱体在传送带上的摆放不能歪斜;另一种是采用机器视觉的方法[1-3],具有非接触、速度快的特点。文献[4]采用单相机和两组线结构光构成视觉系统,利用三维重建的原理测量卷烟包装盒的三维尺寸,该系统测量精度较高,但使用的设备较多。文献[5]利用单相机与2组点结构光组成测量装置,具有灵活、便携的优点,但要求2组点结构光与相机的像平面垂直,且已知两条平行光束间的距离,对设备安装要求高。文献[6]证明,利用长方体本身具有的几何特性,使用一个已标定相机,只需知道在长方体某一个平面上的两个特征点间的实际距离,便可利用长方体顶点的图像坐标获得其三维尺寸。文献[7]实现了一个长方体表面的三维重建,但事先需要人为指定长方体一个顶点的深度值。文献[8]采用了双目视觉的方法,但需要人工选择特征点。

在应用机器视觉的方法中,首先需要从图像中提取出长方体可见的边线或顶点特征,再通过计算特征间距离实现测量。对于长方体边线的提取,典型方法是采用Hough变换从原始图像或原始图像的校正图像中获取直线方程[9],受相机透视投影的影响,长方体边线间的平行和垂直关系在原始图像的校正图像中都不成立,一般是利用消失点和消失线确定直线间的平行关系[1-3,10-11],因此直线间固有的约束不易被利用,容易导致特征提取出现偏差,影响测量精度。

本文提出一种基于投影轮廓的长方体纸箱测量方法,通过一台已标定的相机拍摄的一幅图像实现对目标的三维测量。采用虚拟像平面相机模型,利用相机标定结果生成纸箱在支撑平面上的投影图像,本文称其为虚拟图像,相比于目标在真实像平面的成像,在该虚拟图像上长方体的边线保持了其固有的垂直和平行特性;利用这些特性,通过提取目标的轮廓点构造边线点集,采用最小二乘方法得到虚拟图像上的六条边缘的直线方程;进而获得目标的三维尺寸。

1 长方体透视投影模型

1.1 传统相机模型

理想的相机模型是一个针孔模型,若以齐次坐标的形式表达,世界坐标系中的点(x,y,z,1)与图像中的无畸变对应点(u,v,1)间存在以下关系

(1)

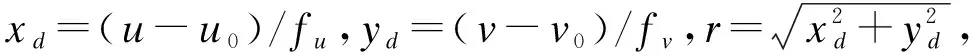
(2)

式中：k1、k2为镜头径向畸变参数；p1、p2为切向畸变参数。采用主流的相机标定方法[12],可获得相机的内外参数及镜头畸变参数。

1.2 长方体投影的基本性质

以相机光心为透视中心,以长方体的支撑面为投影平面,一个三视面的长方体的投影效果如图1所示。

图1中投影平面上的六边形A′B′C′DEF构成长方体的投影轮廓,其中点A′、B′、C′、G′分别是长方体顶点A、B、C、G的投影点,S为相机光心OC在该平面上的垂直投影点。

在投影平面上建立世界坐标系,长方体的投影轮廓线满足以下性质:

性质1.A′B′//DE//C′G′;

性质2.B′C′//EF//A′G′;

性质3.∠A′B′C′=∠DEF=90°;

性质4.A′C′//DF;

性质5.A′F、G′E、C′D相交于S;

性质6.记V为轮廓的内点集合,则

SE=min{SP|P∈V},SB′=max{SP|P∈V}。

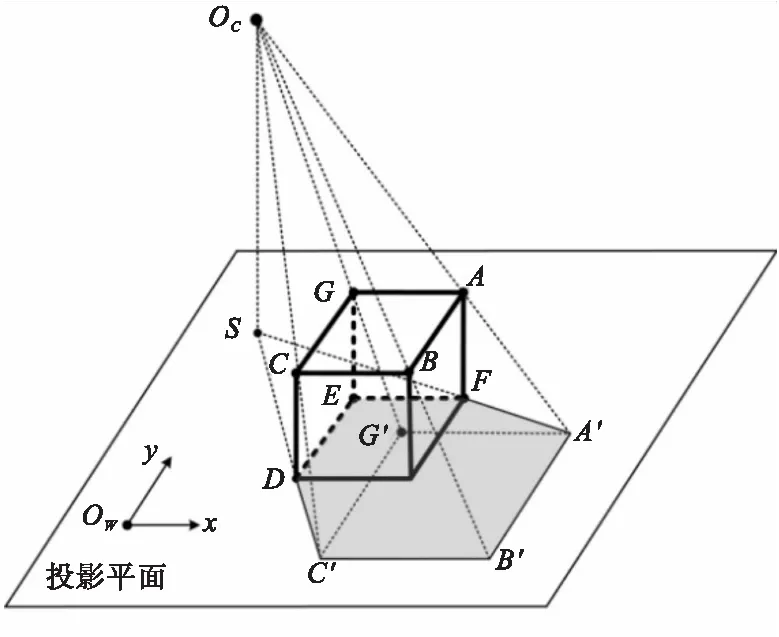
图1 三视面长方体的投影示意图

1.3 投影图像生成

本文利用长方体在支撑平面上的投影图像实现目标的三维尺寸测量,为生成目标在该投影平面的投影图像,首先标定出相机的内参数、相对于所定义的世界坐标系的外参数、镜头畸变参数;再根据视场区域,在投影平面上划分若干等间距网格,若能估计出每个网格点的像素值,则这些网格点构成一幅虚拟图像;由于每个网格点的世界坐标是已知的,可利用公式(1)计算其在真实像平面上的无畸变投影点,再利用公式(2)计算其有畸变图像点,再利用双线性插值方法或双三次插值方法对该网格点的像素值进行估计。

由相机外参数的标定结果也可得到相机光心在世界坐标系下的坐标

(xCyCzC)T=-RT

(3)

由相机光心和虚拟图像构成相机的新的透视模型,本文称其为相机的虚拟像平面模型,该模型中的虚拟主点坐标为(xC,yC),虚拟焦距为zC,虚拟图像的像素距为人为划分的网格间距。由于虚拟图像在生成过程中消除了镜头畸变的影响,因此虚拟图像是一个无镜头畸变的图像,该模型是一个理想的透视模型,针对长方体测量,使用该模型的优点是投影图像中的轮廓边缘直线具有1.2节中描述的便于利用的几何性质。

2 长方体三维尺寸测量

2.1 投影轮廓提取

本文采用机器学习的方法[13-15]从投影图像中提取纸箱的轮廓,将不同种类的纸箱置于场景中,拍摄若干样本图像,对纸箱区域进行人工划分,得到纸箱前景、背景的样本点集,应用具有高斯核函数的支持向量机(Support Vector Machine,SVM)方法[16],获得前、背景分割的分类器,用于提取目标图像中的纸箱区域,再利用中值滤波对前景图像进行滤波,进行边缘提取后得到纸箱的轮廓点,构成轮廓点集U。

从工程应用的角度考虑,为便于纸箱区域提取,可以将测量系统的背景设计得比较简单,并且与纸箱颜色有较大差别,但由于纸箱上有印字等原因,容易导致纸箱轮廓内部区域出现误分割,并导致边缘提取后部分内部点被误划入轮廓点集,因此在轮廓线段样本点集构造过程中应避免这些错误点的影响。

2.2 轮廓线段样本点集构造

为精确提取每条轮廓线段的直线方程,需首先从U中分离构造出各线段的样本点集。本文利用长方体的投影轮廓是一个凸六边形的性质,首先判别某个顶点的位置,再从该顶点出发,利用一维Hough变换的方法构造两个邻边的样本点集。下面以线段DE和EF为例说明构造其对应的点集SDE和SEF的过程。

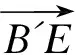
(5)分别以两个候选区间中的轮廓点作为样本点,估算DE和EF的直线方程y=kDEx+bDE和y=kEFx+bEF;

(6)分别对两个候选区间中的每个轮廓点P(xP,yP),计算其到相应直线的距离;

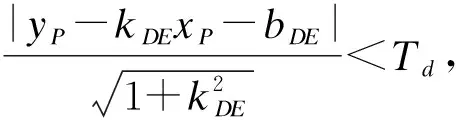
从以上构造过程看,轮廓点集中长方体内部的错误点,并不会对边线点集的构造结果有太大的影响。

2.3 长方体尺寸测量

由性质1、性质2、性质3,受平行与垂直约束,A′B′、B′C′、DE、EF的直线方程可分别表示为

(4)

式中k、bAB、bBC、bDE、bEF为未知参数。

利用采样点集SAB、SBC、SDE、SEF,对公式(4)应用最小二乘法,可获得k、bAB、bBC、bDE、bEF的估计值,得到以上4条直线在世界坐标系中的直线方程。

根据k的估计值对原世界坐标系进行变换,使光心在底面的投影点S为新坐标系的原点,坐标轴分别与ED和EF平行,新坐标系下的轮廓如图2所示。

图2中bA、bD、bF、bC均可通过坐标变换获得,xA、yC的值待定。由性质4和性质5容易得到

(5)

(6)

于是直线SA′在新坐标系下的直线方程为

bAx′-xAy′=0

(7)

直线SC′在新坐标系下的直线方程为

(8)

直线方程(7)和(8)构成对参数xA的线性约束。将点集SFA和SCD内点的坐标转换成新坐标系下的坐标,为简化符号,在不引起歧义的情况下,这里仍用(xP,yP)表示点集内的P点在新坐标系下的坐标。

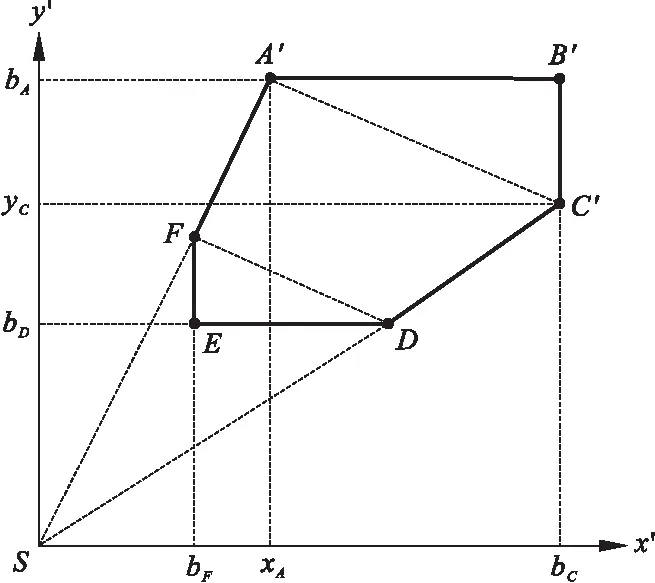
图2 坐标变换后的三视面投影轮廓

利用点集SFA和直线SA′的直线方程(7),应用最小二乘法,可得到xA的近似值

(9)

将SA′和SC′两条直线的方程(7)和(8)表达为近似归一化形式

(10)

此时若将样本点代入公式(10)的约束方程,则约束产生的误差的绝对值近似为样本点到相应直线的距离。利用点集SFA和SCD对公式(10)的约束方程应用最小二乘法可得到xA的估计生的误差的绝对值近似为样本点到相应直线的距离。利用点集SFA和SCD对公式(10)的约束方程应用最小二乘法可得到xA的估计值。

(11)

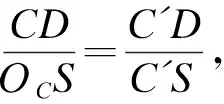
3 实验研究

3.1 长方体尺寸测量仿真实验

设某长方体的三维尺寸为200mm×150mm×100mm,将长方体底面看作是虚拟像平面,并在该平面上根据长方体的底边建立世界坐标系,假设在长方体前方放置相机,相机坐标系相对于世界坐标系x、y、z三个坐标轴的旋转角分别为225°、30°、90°;平移向量为(-150,180,1200)(单位:mm);设相机的内参数为fu=fv=2000,u0=800,v0=600。在长方体可见的6条轮廓线上进行采样,每1mm设置一个采样点,根据采样点在世界坐标系中的空间坐标计算其对应的图像坐标(ui,vi),并计算其投影到虚拟像平面上的坐标(xi,yi)作为长方体轮廓的采样点,图3是这些采样点在虚拟图像上的分布情况。虚拟图像的尺寸为1000×1000像素,像素距为0.5mm。仿真实验中对虚拟图像中的采样点施加服从均匀分布U[-λ,λ]的干扰,这里λ(单位:像素)为干扰强度。利用被干扰后的采样点坐标通过本文的方法提取直线并进行长方体的三维尺寸计算。针对某个干扰强度λ,进行500次仿真实验,对测量结果相对于真实值的误差进行统计,图4是测量平均误差随λ的变化情况,图5是最大误差随λ的变化情况。

从仿真结果看,当λ=0时,算法可准确得到长方体的三维尺寸,说明了本文算法的正确性;误差总体上随着干扰强度的增大而增加,当边缘点提取误差最大达到5个像素时测量最大误差仍能保持在1mm以内,平均误差在0.3mm以内,说明算法具备较好的鲁棒性。

图3 虚拟图像上的采样点

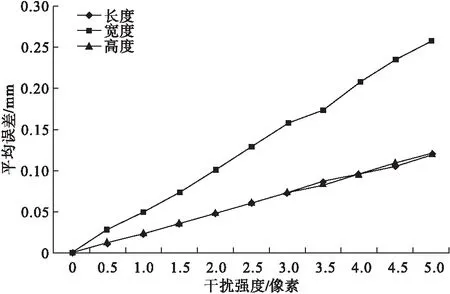
图4 仿真实验中平均误差变化曲线

图5 仿真实验中最大误差变化曲线

3.2 真实纸箱测量实验

本实验选择三个不同规格的纸箱样品,针对每个样品拍摄其在不同位置姿态下的照片各15幅,并利用本文方法进行测量。图6显示了其中三组的实验图像,其中左侧第一列为纸箱原始图像,实验中相机采用Basler acA1600-20gc彩色相机,配12mm工业镜头,目标距相机距离约1m,原始图像的尺寸为1624×1234像素;第二列为对应的虚拟图像,虚拟图像的尺寸为1400×1400像素,像素距为0.5mm;第三列为利用SVM方法分割出的纸箱区域;第四列为利用本文方法最终提取出的六条边缘直线。从图像上看,三种样品在区域分割过程中受标签、胶带反光影响,在纸箱中间和边缘处都出现了误分割;受桌面纹理和阴影的影响,在背景区域也存在误分割,但均未对最终的直线提取产生很大的影响,说明了本文方法具有一定的鲁棒性。

图6 三种纸箱样品的实验图像

表1是针对每个样品测量的误差统计结果。

表1 实际纸箱样品的测量结果 mm

从表1可以看出,实验中对纸箱的三维测量误差在毫米量级,平均相对误差在2%以内,最大相对误差在5%以内,本文算法针对实际纸箱的测量也取得了较好的结果。

将实验结果与现有方法的结果进行对比,根据文献[5-6，8]中的数据,文献[5]采用单目视觉和2组点结构光的方法实现了纸箱三维尺寸的自动化测量,对真实纸箱的测量相对误差在0.20%到11.20%之间;文献[6]采用精确标定的单相机对长方体标准块的测量相对误差在2%以内,但要求手工确定特征点,没有达到本文自动化处理的水平;文献[8] 采用双目视觉并手工选择特征点的方法,对纸箱的测量相对误差在1.5%到11.7%之间。综合以上对比结果,本文方法的测量精度不低于现有最好的方法,在测量系统结构的简单性、自动化程度、鲁棒性等方面都具有优势。

4 结束语

本文提出一种利用长方体纸箱本身具有的几何约束,通过单相机对其进行三维尺寸测量的方法,该方法建立了目标在支撑平面上的投影图像,不仅实现了镜头畸变校正,还保持了长方体轮廓线间固有的平行和垂直约束关系,通过合理运用这些约束进行边缘直线特征提取,有利于提高测量精度。仿真和真实实验都证明该方法具有一定的鲁棒性。该方法仅需一台已标定相机完成测量,视觉系统结构简单,适用于对传送带上的长方体纸箱进行三维尺寸测量。