舰船甲板挠曲变形动态检测技术研究

任 波,李天姣,王显强,迟秀秀

(沈阳理工大学 装备工程学院,沈阳 110159)

航空母舰是一种以舰载机为作战武器的大型水面舰艇,可以供舰载机起飞和降落。为保证舰载机正常飞行和着舰,需要提供给其一定精度的姿态、位置及运动参数等信息[1]。由于航母的长度过长(达300m以上),航行时会发生船体变形,甲板的变形会更为显著。当甲板形变量在小范围内,着舰影响小;当甲板形变量超出设计规格,将产生两种严重后果:①飞机撞击航母;②飞机掉进海里。所以要对舰船甲板形变量进行动态检测。

常用的船体变形测量技术主要包括:偏振光能量测量法、大钢管基准法、双光源双CCD测量法、双频偏振光法、光栅法、液体压力测量法、摄影测量法、应变传感器测量法、多部位安装航姿系统、惯性测量匹配法以及GPS测量法等等[2]。本文采用INS和SINS组合导航方法研究甲板变形参数,这种方法既可实时进行,也可测后实时,本文采用的是测后实时;通过卡尔曼滤波算法处理测量数据,降低噪声干扰;根据微分几何求得甲板挠曲真实姿态,当甲板的形变量超过设计指标既可及时对甲板进行修复。

1 甲板变形检测系统原理

在舰船甲板变形问题中,需要知道甲板上各点处的局部挠曲变形参数,将测量得到的数据与原设计值比较,如果超过限制就认为该点处是飞机潜在危险着舰点;找出该点位置坐标既可进行相应的维修。INS安装在舰船上作为基准,提供舰船的位置、速度和姿态信息[3]。将SINS放置在舰船甲板尾端使其匀速运行至舰首,将获得的数据进行处理与分析,与INS的姿态信息做差,再利用微分几何知识求得甲板的曲率与挠率,根据曲率挠率参数探测事故段,同时得到事故段的位置坐标,示意图如图1所示。

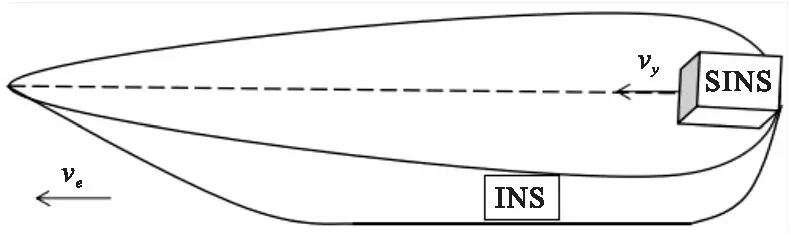
图1 INS和SINS位置示意图

曲率k反映曲线的弯曲程度,挠率τ反映曲线的扭曲程度[4]。

(1)

(2)

(3)

式中x、y、z为SINS系统的坐标轴方向。

2 INS系统建模

本文选用地理坐标系建立INS导航方程,主要由于地理坐标系的三个坐标轴分别沿当地纬度线指向正东、沿当地子午线指向正北、沿当地参考椭球的法线指向天空。所以,利用地理坐标系力学编排方程,作为系统输出的导航参数,可直接得到舰船的地理坐标,即纬度、经度、高度,表示为(φ,λ,h)[5]。

2.1 INS状态方程的建立

取舰船在海中位置rL的状态变量为

rL=[φλh]T

(4)

在地理坐标系里表示速度vL的状态变量为

vL=[vevnvu]T

(5)

式中e、n、u分别代表东向、北向、天向。

将式(4)两边进行微分,可得位置变化率与运动速度的关系式

(6)

式中D为位置变化率与运动速度的转换矩阵,可由式(7)计算。

(7)

式中,M、N分别为大地子午圈、卯酉圈的曲率半径。

M≈Re(1-2ε+3εsin2φ)
N≈Re(1+εsin2φ)

(8)

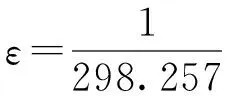
对式(5)两边求导,得

(9)

(10)

解矩阵微分方程得

(11)

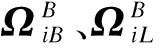
(12)

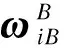
(13)

式中ωe为地球自转角速度。

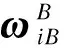
(14)

式中:P=diag(αt)、Q=diag(βt)为对角阵;αt、βt为相应随机过程的反相关时间;t为维数(t=3)。

组合式(6)、(9)、(11)、(14),可得当地水平坐标系中捷联惯导系统的状态空间模型为

[WrWv+gLWRWdWb]T

(15)

式(15)将状态向量XL的15维状态简写成5维,给出了当地水平坐标系中的力学编排方程,Wr、Wv、WR均为白噪声向量。这个导航方程的输出包括地理坐标(φ,λ,h)、速度(ve,vn,vu)和姿态角信息(翻滚角γ,俯仰角p,航向角y)。

(16)

2.2 INS观测方程的建立

将INS力学编排输出的角速度以及比力作为测量信息,按照5维状态方程列写INS的观测方程

Z1=H1XL+V1

(17)

H1=[0(2×3)I(2×2)]

(18)

式中:Z1为观测向量;H1为观测矩阵;I为单位矩阵;V1为观测噪声。

3 SINS系统建模

如图1所示,SINS在甲板上滑动,舰首方向为y轴,垂直甲板向上为z轴,x轴由右手螺旋定则确定,建立SINS导航方程。

3.1 SNIS状态方程的建立

与INS不同,描述舰船甲板挠曲角运动的模型至少为二阶,为尽量降低卡尔曼滤波器的阶数,这里取二阶模型,变形角为σn,相应的变形角速度为ωσn,n=x、y、z,ρ为相应随机过程的反相关时间,则二阶模型为[7]

(19)

式中Wσn为白噪声。

状态方程如下

(20)

式中WS为系统噪声。其中状态向量Xs含距离rn、速度vn、变形角σn及角速度ωσn等12个状态。

Xs=[rxryrzvxvyvzσxσyσzωσxωσyωσz]T

(21)

状态转移矩阵F为

(22)

3.2 SNIS观测方程的建立

利用陀螺仪测量SINS角速度变化,观测方程如下

Z2=H2Xs+V2

(23)

H2=[0(3×9)I(3×3)]

(24)

式中:Z2为观测向量;H2为观测矩阵;V2为观测噪声。

4 仿真

4.1 卡尔曼滤波算法

卡尔曼滤波用状态方程和递推方法进行估计,根据前一个估计值和最近一个测量数据来估计信号的当前值,其解以估计值的形式给出。卡尔曼滤波算法如下[8]。

(25)

式中:Xk是系统的n维状态向量;Zk是系统的m维观测序列;Φk,k-1为状态转移矩阵;Hk为观测矩阵;Jk是系统噪声Wk的对称非负定方差矩阵;Γk为观测噪声Vk的对称正定方差阵;假设Wk和Vk是互不相关的零均值白噪声。

4.2 仿真参数设定

本文以“辽宁号”航母为仿真对象,舰长304.5m,设飞行甲板300m作为SINS仿真长度。滤波周期选1s,仿真时长选100s,舰船在海中向东行驶,初速为10kn,纬度100°,经度30°,翻滚角、

俯仰角、航向角均为0.1°,陀螺仪初值均为1rad/s,东向加速度为1m/s2。SINS沿y方向以3m/s速度匀速行驶。

4.3 仿真结果分析

INS和SINS的姿态角和旋转角速度滤波前后的仿真结果如图2所示。

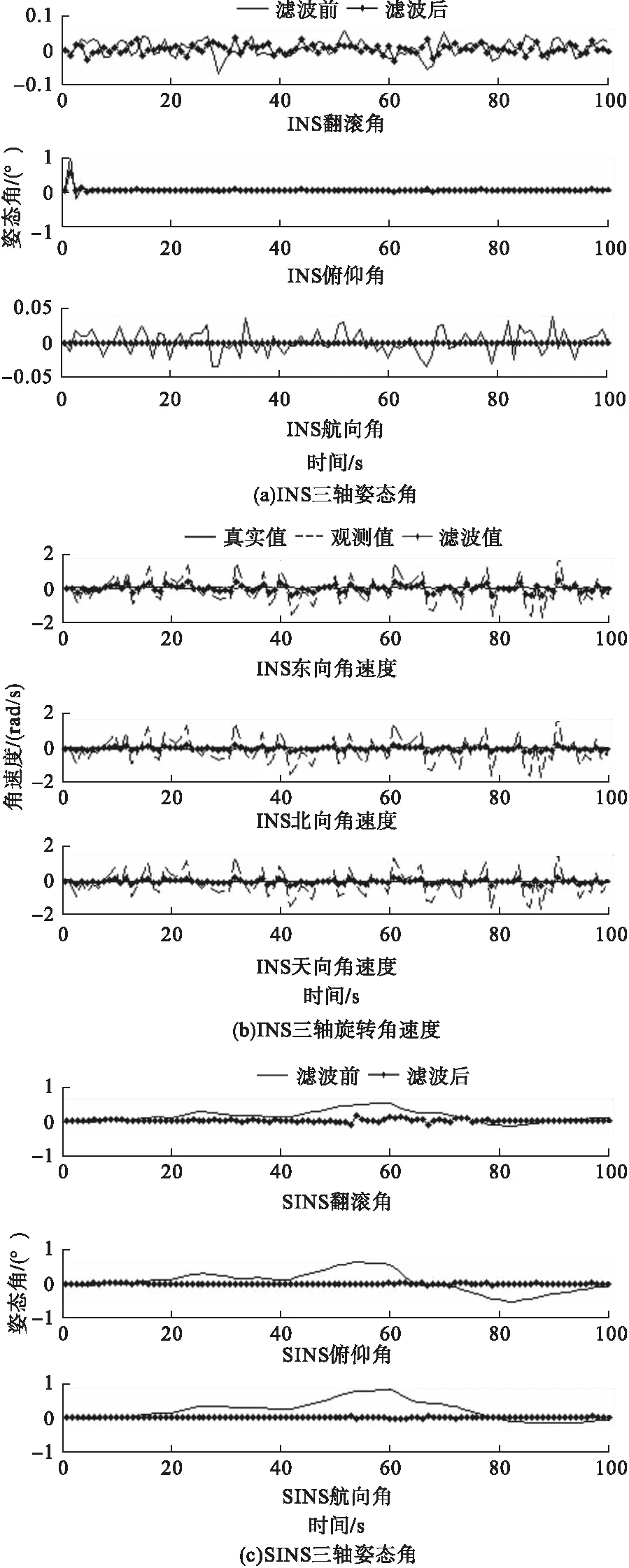
图2 INS和SINS姿态角和旋转角速度

图2a是INS的姿态角,从图2a可以看出,卡尔曼滤波对航向角的滤波最快、效果好,对翻滚角和俯仰角的滤波效果稍差。图2b中滤波前的东向角速度偏差最大接近2rad/s,滤波后的角速度偏差降低到0.5rad/s以下;滤波前的北向及天向角速度偏差最大均接近3rad/s,滤波后的角速度偏差均降低到0.4rad/s以下。由图2c可以看出,噪声对姿态角影响很大,故对SINS姿态角去噪很重要,同时可以看出卡尔曼滤波效果很好。图2d中SINS的旋转角速度要比图2b中小一些,但滤波效果相同。由图2可以看出,卡尔曼滤波对舰船两惯导系统都有很好的降低噪声的作用,降低了观测误差,使对舰船姿态的观测更精准。

根据微分几何得到舰船甲板曲率、挠率如图3所示。

由图3可以看出舰船在海中航行时,挠率大于曲率,这与预想的结果一致。舰船前端受力面积小,所以要使船上下摆动并不容易,相应的曲率就较小;但船体长,侧面面积大,那么使甲板发生

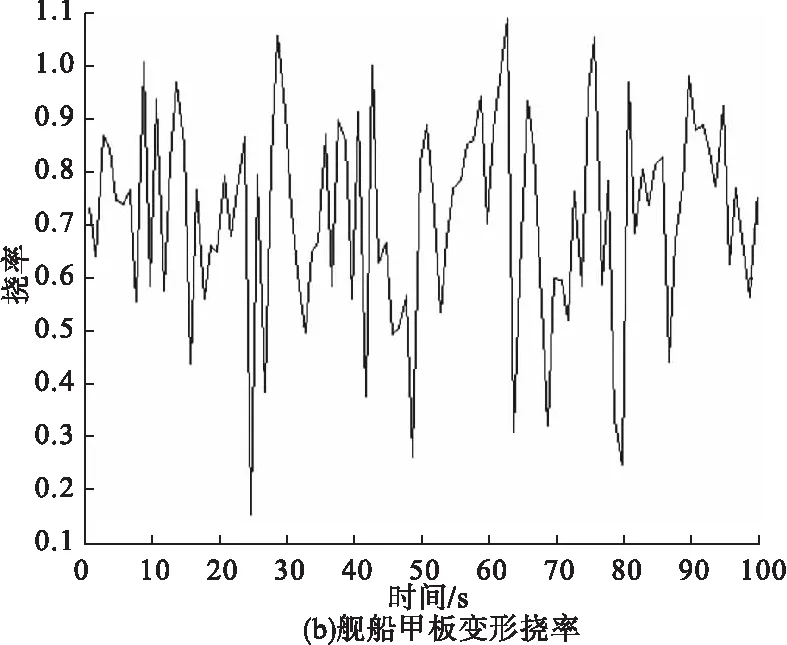
图3 甲板曲率挠率形变量

扭曲相对来说比较容易,相应的挠率就较大。将舰船甲板形变量与甲板设计参数进行比对,超出设计范围即为潜在危险处,找到危险处对应的时刻,对其相应的位置进行修复。

图4为SINS在甲板上的运行速度及相应位置图像。

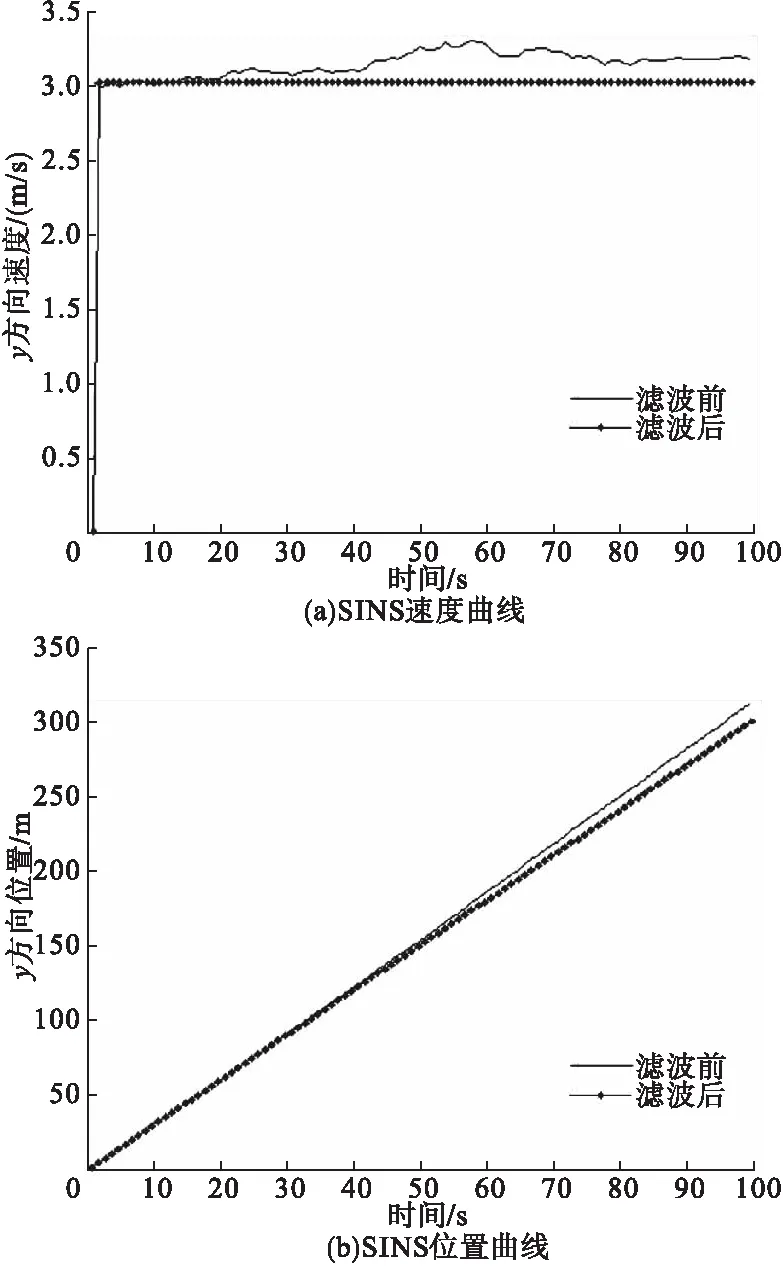
图4 SINS速度与位置曲线

由图3查出超出曲率挠率设计指标的对应时刻,根据此时刻既能找到图4中对应位置,此处即为甲板上的潜在危险处。

5 结论

采用了卡尔曼滤波方法对数据去噪,经过少数几次迭代后,卡尔曼滤波值接近真实值,误差降低到原来的四分之一,极大限度地降低了噪声的影响,检测精度提高,说明了这种方法对舰船甲板变形的检测是较好的。后期将会尝试结合小波多尺度变换去噪,观察去噪效果是否更好。