基于智能神经网络的模糊数字识别研究

贺笃贵，邢兵锁

(铜陵职业技术学院，安徽 铜陵 244000)

一、引言

数字识别是模式识别的一个重要应用分支，近年来，被广泛研究及应用于各个领域。比如应用在车辆牌照的自动扫描识别、证件数字的扫描、表格数字的识别等。但是由于某些人为或者自然因素的存在，导致原始扫描的数据缺损或变形，此时对数字识别技术的要求将大大提高，因此需要更加智能的方法去除干扰项。目前我们常用的数字识别方法是首先从已有图片中提取初始数据，其次再把由图像中初步提取的数字串分解成较简单的单个字符，最后使用分类器进行进一步识别[1]。目前常用的分类器有最近邻分类器以及多分类组合方法、人工智能的方法等。

在众多智能分类方法中，人工神经网络分类方法具有高度的识别分类功能，能够识别字符较集中的字符串以及噪声较高的字符，误差较小，是近年来学者们研究的重点。Hopfield神经网络是美国物理学家J.J Hopfield在1982年提出的，该网络是一种递归神经网络，具有强大的联想记忆功能，在一定的干扰的情况下能够对数字进行准确地识别，因此被广泛应用于图像信息识别、信号数据处理、声音数据处理、模式分类、数据查询等[2]。

离散Hopfield神经网络具有较好地联想记忆功能，当遇到一些带有噪声的数字或者车牌时，可以摒弃噪声的干扰，准确地识别初始数字，因此在实际数字提取中具有很高地应用性[3]。本文根据离散Hopfield神经网络强大的联想记忆特性，对将其应用于模糊数字识别系统进行了研究，从而实现数字噪音的去除，提取数字关键信息。

二、离散Hopfield网络模型

离散Hopfield神经网络可认为是一种单层、输出分别为-1和1两个固定数值的离散型反馈神经网络[4]。图1所示为典型离散Hopfield神经网络的基本结构构成。

图1中第0层神经元并无计算功能，只是作为神经网络的输入层。图中所示的第1层神经元起到对第0层传输的信息进行加工再处理的作用，因此认为是真正的神经元。第1层的神经元首先对接收的输入层信息进行加权求和，再经过神经元作用函数进一步处理产生输出，作用函数一般选用阈值函数，即该层神经元的输入达到阈值则输出为1，达不到阈值则输出为-1，因此网络的输出为离散数值，称神经网络为离散Hopfield神经网络。图1中n1,n2,…nn表示Hopfield神经网络的输入值，a1,a2,…an表示该神经网络的n维输出值，wij为神经元之间的连接权值，其表示第0层神经元i到第1层神经元j的连接权值[5]。

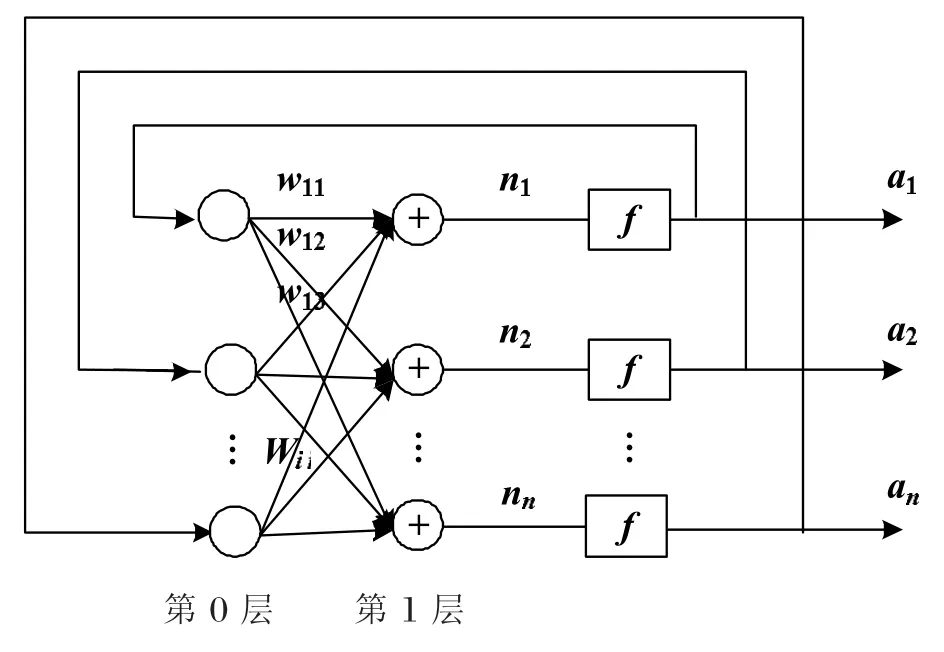
图1 离散Hopfield神经网络结构

在图1中可以形象的看出离散Hopfield网络输出信息反馈到输入端，是一种典型的反馈型神经网络；当给定图中Hopfield神经网络第0层的输入值后，信息经过网络中间各神经元函数的处理产生输出信息，输出信息再反馈到输入端，信息流再经过神经网络中间神经元的处理，得到新的输出信息，信息经过反复不断处理，直到神经网络的输出值不再变化，此时认为系统达到稳定，此时神经网络的输出值为恒定值。对于准确建立一个网络模型而言，最重要的是找出网络达到稳定时各神经元之间的连接权值wij。

三、数字识别模型建立

准确建立离散Hopfield神经网络模型的关键是确定当网络输出稳定时各神经元之间的连接权值，其具体过程如下[6]：

图1中,假设离散Hopfield神经网络第j个神经元的输入值为：

图中神经网络第1层的神经元的激活函数为阈值函数，此时可根据阈值函数性质得到第j个神经元的输出值为：

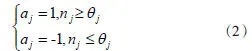
此时，可根据神经网络的输出为所有输出神经元信息的代数集合。对于有n个神经元的Hopfield神经网络，其输出在t时刻的相量为：A(t)=[a1(t),a2(t),…,an(t)]。

同时可以计算出神经网络在t+1时刻的输出状态为：

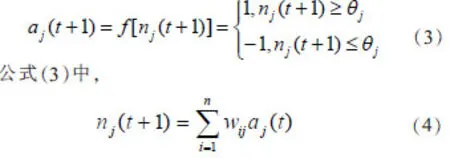
上述是离散Hopfield神经网络迭代过程中使用的基本公式，按照动力学的演化方式，神经元将不断改变其状态，即按照“能量”的减小方向不断迭代，直到达到稳定状态，网络输出不再改变，此时的稳定状态即为神经网络的期望输出。

假设Z(t)=[z1(t),z2(t),…zn(t)]为网络的稳定输出点，则设能量函数的变量为：

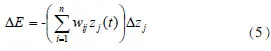
神经网络具体的运行步骤如下：

Step1：神经网络参数的初始化 （可利用MATLAB自带的工具箱函数建立单层的Hopfield网络）；

Step2：输入神经网络的稳定输出样本Z(t)=[z1(t),z2(t),…zn(t)]，计算网络权值，并在后续步骤中一直保持不变；

Step3：输入网络带噪声的初始输入值;

Step4：根据串行工作方式迭代计算，随机地更新某一个神经元的输出状态。

Step5：判断网络是否达到稳定状态，若出现输出aj(t)在某一时刻开始，状态不再发生变化，则认为网络处于稳定状态。

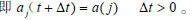
Hopfield神经网络运行的具体流程图如下：

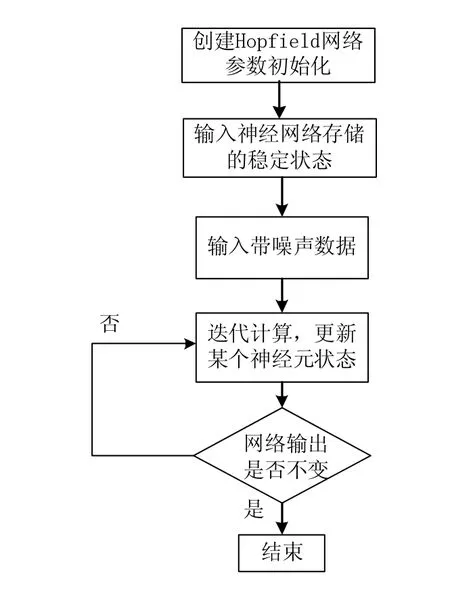
图2 Hopfield神经网络运行流程图

四、Hopfield神经网络数字模式识别

离散Hopfield特质显著，文中将运用其识别带有固定噪声的 10 个数字 0，1，2，3，4，5，6，7，8，9 以及带有随机噪声的 0，1，2，3，4，5，6，7，8，9， 即构建的Hopfield神经网络模型稳定输出点为上述十个数字，通过训练使网络稳定到上述的十个数字点。在本实验中网络输出由0～9这10个数字稳态构成，每个稳态数字用10*10的矩阵点表示，该矩阵可以比较直观地展示数字，由于Hopfield网络对这10个数字的稳态输出点具有联想记忆的功能，当数字带有噪声时，网络模型可以摒弃噪声识别数字。文中选用两种产生噪声的方法，一种是给定某一数字固定的噪声。在本次实验中选用数字1,2,3给定固定噪声点；另一种是通过编写MATLAB程序产生随机噪声。在本实验中为了便于比较仍然选用对数字1,2,3产生随机噪声点，同时观察网络对不同级别的噪声的识别能力。

实验在MATLAB工作环境下进行，采用MATLAB软件中自带的Hopfield函数建立识别模型。通过建立的实验模型对噪声进行识别，本实验共识别两组噪声[8]：首先是识别带有一定固定噪声的数字1,2,3，结果如图3所示，图中共有三行数字，第一行是标准数字，即网络的稳定输出点，第二行表示给定的噪声数字，第三行表示神经网络模型实际的输出识别数字。从实验结果可知，Hopfield神经网络模型对带有一定固定噪声数字的识别能力较强，识别的数字非常接近标准数字。

图3 固定噪声识别结果

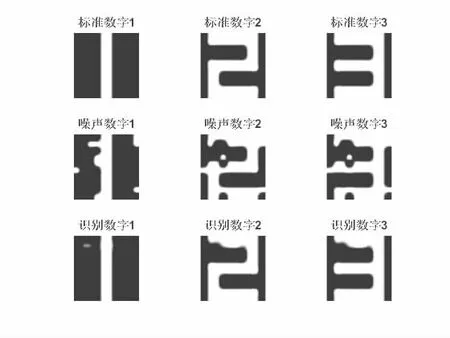
图4 噪声比10%识别结果

图5 噪声比20%识别结果

图6 噪声比30%识别结果

随后，识别带有随机噪声的1,2,3数字，为了进一步测试神经网络模型的识别能力，根据噪声比（噪声点数占总矩阵点数的比重）的由少及多分别测试。其中图4显示的是噪声比为10%时的测试结果，结果显示模型识别能力较强。图5显示的是噪声比为20%时的测试结果，结果显示具有一定的数字识别能力，但是精度较低。图6显示的是噪声比为30%时的测试结果，可以看出模型此时的识别能力非常弱。图7显示的是噪声比为40%时的测试结果，从该结果可以看出此时模型识别的数字非常模糊，去除噪声能力非常弱，对数字的识别能力差。

五、结论

文中运用离散Hopfield神经网络构建数字识别模型，分别识别带有固定噪声的0-9十个数字以及不同噪声比的0-9十个数字。结果显示，模型对带有一定固定噪声和噪声比较低的随机噪声数字时识别能力较强，因此该模型在模糊数字识别中具有一定的应用性。但当噪声比较高时，模型几乎很难识别这些数字，模型失效。因此，针对高噪声的数据，后期考虑对模型进行改进，提高识别精度。从而对其在今后实际数字提取方面的应用中提供一定的帮助。

图7 噪声比40%识别结果