对一道经典分割问题的探究

段广猛

（江苏省高邮市赞化学校）

如果一个三角形恰好能够被分割成两个等腰三角形，那么这个三角形应该满足怎样的条件？并且如何分割呢？

一、问题解决

对于如此抽象的问题，笔者的解决方案按以下步骤逐一展开，此为思维的有序性.

1.大小假设

如图1，在△ABC中，不妨设∠A≤∠B≤∠C，即∠A为最小角，∠C为最大角.

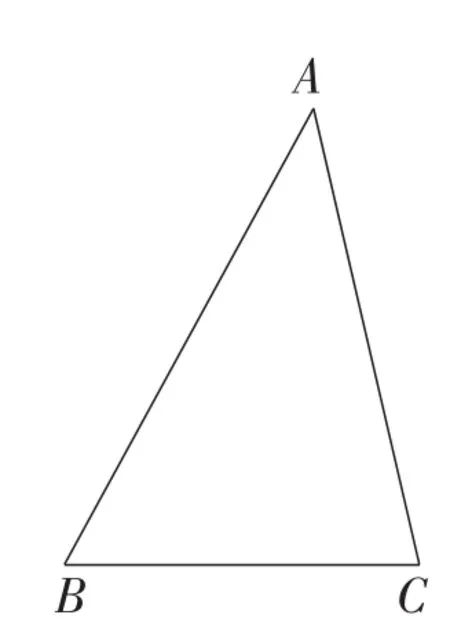
图1

2.总体策略

逆向思考，反道而行；画出草图，精准分析.

3.局部策略

先通过观察做定性分析，缩小范围，再分类做定量研究.

4.分类决策

分三类解决问题：第一类是过最小角∠A的顶点分割；第二类是过较大角∠B的顶点分割；第三类是过最大角∠C的顶点分割.

5.实施过程

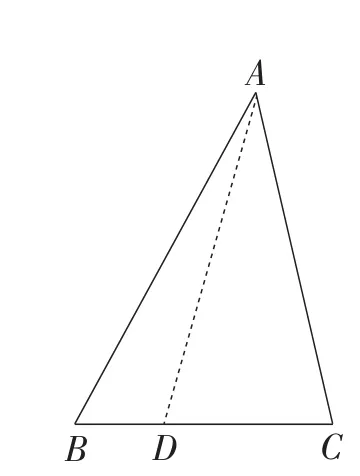
图2

第一类：如图2，当过最小角∠A的顶点作分割线AD时，易得∠ADB＞∠C≥∠B≥∠BAC＞∠BAD.锁定△ABD，即∠ADB＞∠B＞∠BAD，故△ABD不可能为等腰三角形，可得结论1.

结论1：对于任意三角形，过最小角的顶点都不能分割成两个等腰三角形.

第二类：如图3，当过较大角∠B的顶点作分割线BD时，易得∠ADB＞∠C≥∠ABC≥∠A.锁定△ABD，则有∠ADB＞∠ABD，且∠ADB＞∠A.故要使△ABD为等腰三角形，只有一种可能，即∠ABD=∠A.

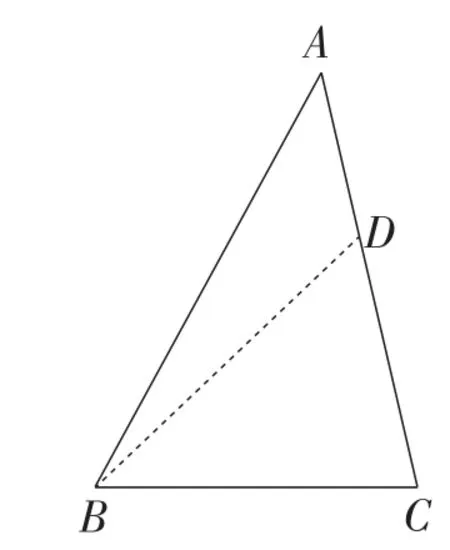
图3

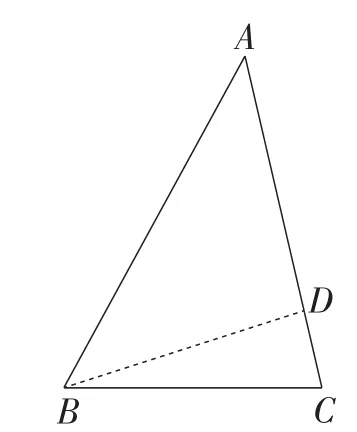
图4

接下来调整图形.如图4，∠ABD=∠A，继续观察做定性分析，锁定△BCD，易知∠C≥∠ABC＞∠CBD，故要使△BCD为等腰三角形，有两种情况，即∠C=∠CDB或∠CBD=∠CDB.

情况1：如图5，当∠C=∠CDB时，设∠ABD=∠A=α，则∠C=∠CDB=2α，∠DBC=180°-4α，∠ABC=180°-3α..

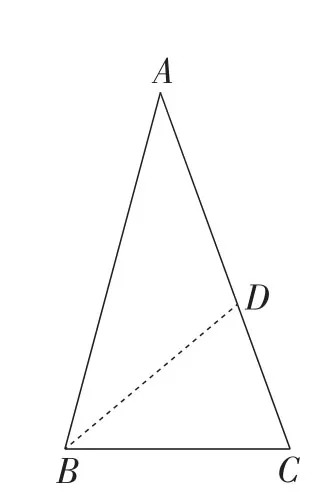
图5

分析定量关系：由∠A≤∠ABC≤ ∠C及∠DBC＞0°，则有解得36°≤α＜45°.

有趣的是，此时还会发现∠C=2∠A，从而可以得到以下结论.

结论2：当某三角形同时满足36°≤最小角α＜45°，且存在另一个角2α时，只需要过第三个角的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.

情况2：如图6，当∠CBD=∠CDB时，设∠ABD=∠A=α，则∠CBD=∠CDB=2α，∠C=180°-4α，∠ABC=3α..

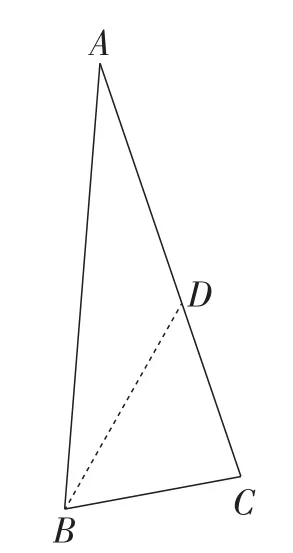
图6

分析定量关系：由∠A≤∠ABC≤∠C，则有解得.

有趣的是，此时还会发现∠ABC=3∠A，从而可以得到以下结论.

结论3：当某三角形同时满足最小角，存在另一个角3α时，只需要过角3α的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.

图7

第三类：如图7，当过最大角∠C的顶点作分割线CD时，易得∠ADC＞∠B≥∠A. 锁 定 △ACD，则有∠ADC＞∠A.故要使△ACD为等腰三角形，又分两种类型，即∠ACD=∠A或∠ACD=∠ADC.

类型1：当∠ACD=∠A时，再锁定△BCD，继续观察做定性分析，但得不到任何有效信息来缩小范围.要使△BCD为等腰三角形，可能有三种情形，即∠BCD=∠B或∠BDC=∠B或∠BCD=∠BDC.

情况1：如图8，当∠BCD=∠B时，设∠ACD=∠A=α，则∠BDC=2α，∠BCD=∠B=90°-α，所以∠ACB=90°，即△ACB为直角三角形.

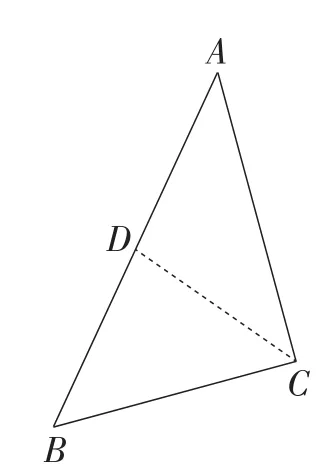
图8

结论4：直角三角形一定可以分割成两个等腰三角形（只需沿着斜边的中线进行分割）.

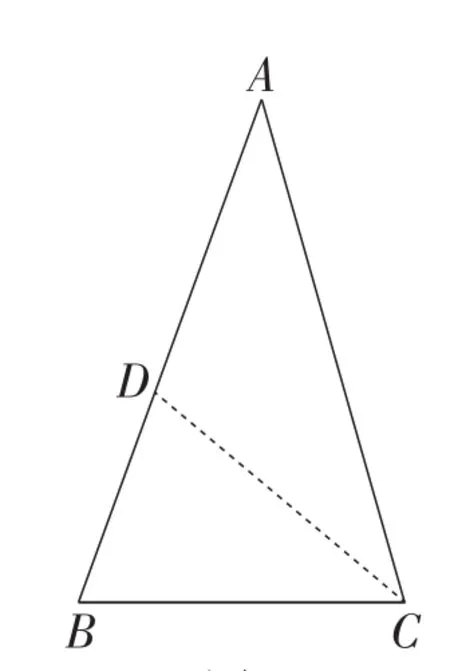
图9

情况2：如图9，当∠BDC=∠B时，设∠ACD=∠A=α，则∠BDC=∠B=2α，∠BCD=180°-4α，∠ACB=180°-3α.

分析定量关系：由∠ABC≤∠ACB， 且 ∠BCD＞0°， 则 有解得α≤36°.

有趣的是，此时还会发现∠B=2∠A，从而可以得到以下结论.

结论5：当某三角形同时满足最小角α≤36°，且存在另一个角2α时，只需过第三个角的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.

情况3：如图10，当∠BCD=∠BDC时，设∠ACD=∠A=α，则∠BCD=∠BDC=2α，∠B=180°-4α，∠ACB=3α.

分析定量关系：由∠A≤∠B≤∠ACB，则有解得.

有趣的是，此时还会发现∠ACB=3∠A，从而可以得到以下结论.

结论6：当某三角形同时满足最小角α≤36°，且存在另一个角3α时，只需要过角3α的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.

类型2：如图11，当∠ACD=∠ADC时，再锁定△BCD，继续观察做定性分析，易知∠BDC＞∠ACD，即∠BDC＞∠ADC，从而∠BDC＞90°.要使钝角△BCD为等腰三角形，只有一种可能，即∠BCD=∠B.

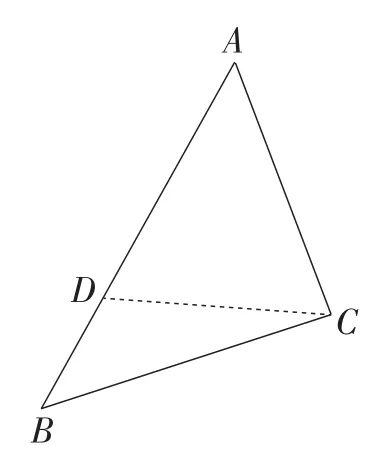
图11

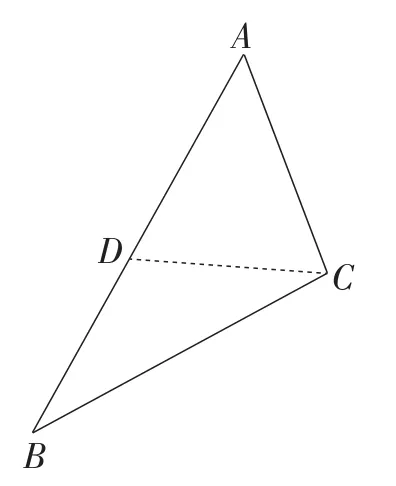
图12

如图12为调整后的图形，设∠A=α，则∠ACD=.

分析定量关系：由 ∠A≤∠B，则有，解得α≤36°.

有趣的是，此时有∠ACB=∠ACD+∠BCD=2∠B+∠B=3∠B，从而可以得到以下结论.

结论7：当某三角形同时满足最小角α≤36°，且另两个角之间存在三倍关系时，可以过三倍角（即最大角）的顶点将原三角形分割成两个等腰三角形.

6.整合结论

为表述方便，可做如下规定：若某三角形有一个内角是另一个内角的二倍，则称此内角为“二倍角”；若某三角形有一个内角是另一个内角的三倍，则称此内角为“三倍角”.

整合分析上述7个结论，进而解决以下两个关键性问题.

问题1：哪些三角形可以被分割成两个等腰三角形？

直角三角形都可以分割成两个等腰三角形（来源于结论4）；

对于非直角三角形，只有当其存在二倍角或三倍角时，才有可能被分割成两个等腰三角形，具体如下.

（1）当某个非直角三角形存在二倍角时，且其最小角α＜45°时，它可以被分割成两个等腰三角形（来源于结论2与结论5）；

（2）当某个非直角三角形存在三倍角时，且其最小角α≤36°时，它可以被分割成两个等腰三角形（来源于结论3、结论6和结论7）.

问题2：对于符合上述条件的三角形，如何分割？或者说分割策略有哪些？

对于直角三角形，可以沿着斜边的中线，将其分割成两个等腰三角形；

而对于非直角三角形，有以下分割策略.

（1）最小角不分割，即不能过最小角的顶点分割（来源于结论1）；

（2）二倍角不分割（来源于结论2与结论5）；

（3）三倍角必分割（来源于结论3、结论6和结论7）.

特别说明：（2）和（3）成立的前提是原三角形中有唯一的二倍角或者三倍角.

若该三角形中存在着两个二倍角或者三倍角，可以选择其中一个进行分割即可，其实这样的三角形有且只有两个，其内角分别为36°，72°，72°或，.

这里的“收网行动”，充分体现了思维的整合性和灵活性，对于学生能力的要求较高，而且得到的结论是解决相关问题的重要“法宝”.

二、实战分析

万事俱备，只欠实战.下面笔者略举几例，来体悟上述所得结果在解题中的应用.

例1如图13，试用一条直线将△ABC分割成两个等腰三角形，其中∠A=40°，∠B=20°.

图13

简析：首先，该直线必过△ABC的某个顶点，否则会割出一个四边形；其次，此△ABC的最小角∠B=20°＜36°，且∠C=3∠A，∠A=2∠B，即它既存在三倍角，又存在二倍角，故必可分割成两个等腰三角形.

最小角不分割，即不能过最小角∠B分割；

二倍角不分割，即不能过二倍角∠A分割；

三倍角必分割，即必须过三倍角∠C来分割.

由此，如图14及图15所示，此题有两种分割方案，问题得解.

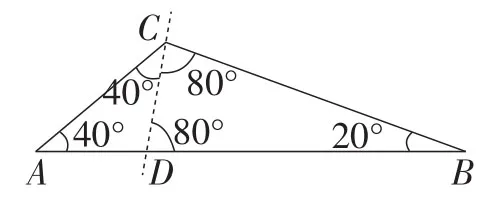
图14

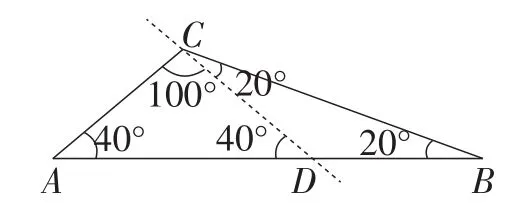
图15

例2给定一张等腰三角形纸片，剪一刀后被分成了两张等腰三角形纸片，求原等腰三角形纸片的各内角的度数.

简析：（1）若此等腰三角形为等腰直角三角形，则可以沿着斜边的中线分割成两个等腰三角形.如图16，此时其各内角的度数分别为45°，45°和90°.

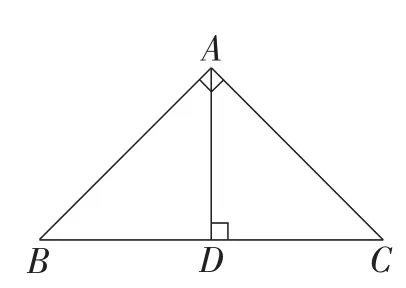
图16

（2）若此等腰三角形为非直角三角形，则其必然含有二倍角或者三倍角，具体可分以下四类.

①当其顶角为底角的2倍时，设底角为α，顶角为2α，则有α+α+2α=180°，解得α=45°.此时它依然为等腰直角三角形，与前面重复.

②当其底角为顶角的2倍时，设顶角为α，底角为2α，则有2α+2α+α=180°，解得α=36°.此时最小角α＜45°，故可以分割.如图17，其各内角的度数分别为36°，72°和72°，即为黄金三角形.

③当其顶角为底角的3倍时，设底角为α，顶角为3α，则有α+α+3α=180°，解得α=36°.此时最小角α=36°，故可以分割.如图18，其各内角的度数分别为36°，36°和108°，仍为黄金三角形.

④当其底角为顶角的3倍时，设顶角为α，底角为3α，则有3α+3α+α=180°，解得.此时最小角α＜36°，故可以分割.如图19，其各内角的度数分别为.

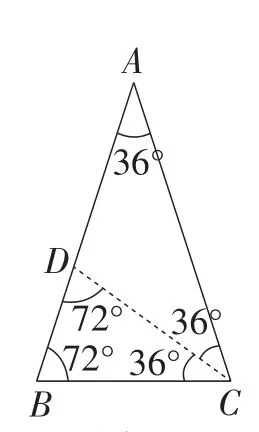
图17

图18

图19

综上所述：符合条件的等腰三角形有四种，其各内角的度数分别为45°，45°，90°或36°，72°，72°或36°，36°，108°或，问题得解.

由实战分析可以看出，本文探索得出的结论对于解决相关的分割问题有极大的作用.但本文最大的价值还是体现在探索数学的乐趣中，这种过程性的享受与收获是笔者更愿意传递的信念与精神.