挖掘基本图形 突破思维节点——对2018年浙江省温州市中考试卷第24题的思考

俞卫胜，吕小玲

（浙江省乐清市育英寄宿学校；浙江省温州市第二十一中学）

2018年浙江温州中考试卷第24题，考查了学生的逻辑推理能力、综合运用知识能力和探究能力，考查了学生在变化过程中对图形的分析能力，考查了学生对基本图形的挖掘能力.试题以动态问题为载体，以问题串的形式呈现，在解法上凸显出了多样性.笔者有幸参与此题的阅卷工作，现结合阅卷的感悟，从试题呈现、试题特色、思路探析、解法赏析几个方面进行思考，并整理成文，与读者分享与研讨.

一、试题呈现

题目如图1，已知点P为锐角∠MAN内部一点，过点P作PB⊥AM于点B，PC⊥AN于点C，以PB为直径作⊙O，交直线CP于点D，连接AP，BD，AP交⊙O于点E.

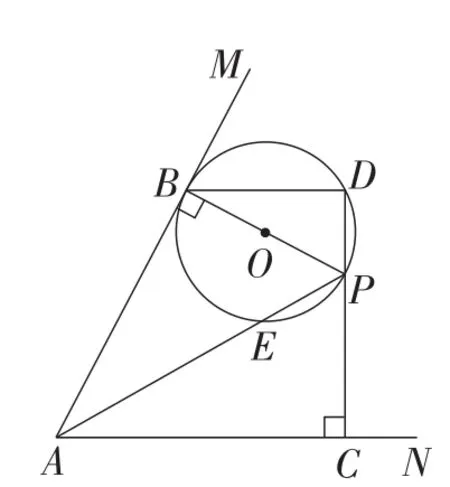
图1

（1）求证：∠BPD=∠BAC．

（2） 连接EB，ED，当时，在点P的整个运动过程中．

①若∠BDE=45°，求PD的长．

②若△BED为等腰三角形，求所有满足条件的BD的长．

（3）连接OC，EC，OC交AP于点F，当tan∠MAN=1，OC∥BE时，记△OFP的面积为S1，△CFE的面积为S2，试写出的值．

二、试题特色

此题属于动态探究性综合题，由一个变化的角牵制线与线的关系，变化的点带动一组线的变化，看似无序的运动，实则动中有静，变中有不变，实现了动与静的完美融合.试题通过分层设问，逐步递进，将三角形、圆、三角函数、方程、轴对称等初中数学的核心知识融为一体，蕴藏着许多经典的基本图形，要求学生通过阅读理解、推理计算、分类讨论等方式进行研究，对学生基础知识的掌握情况、数学思考能力，以及逻辑推理能力都有较高要求，充分体现了“知识与能力并重，思想与方法交融”的特点，凸显数学本质.

三、思路探析及解法赏析

1.第（1）小题思路探析

此小题要证两个角相等，从所给条件及图形来看，寻找或构造一对全等三角形来证明两个角相等这个途径比较困难.于是想到找第三者建立两个角之间的联系，可以通过∠BPC架起∠BPD与∠BAC的桥梁，如解法1，也可以通过等角进行转移，如解法2.当然，若能挖掘A，C，P，B四点共圆这个隐含信息，利用圆内接四边形这个基本图形亦可解决.

除了通过现有的角建立两者的联系外，还可以通过作辅助线构造基本图形，寻找它们之间的联系.由∠ABP=90°，想到构造“三垂图”，实现角的转移，如解法3.由BD∥AC想到构造“X型”“A型”相似图，如解法4和解法5.在教学中，教师要引导学生从多角度思考问题，提倡一题多解，多解归一，可以提升学生的逻辑推理能力，加深学生对数学本质的理解.

解法1：如图2，因为PB⊥AM，PC⊥AN.

所以∠ABP+∠ACP=90°+90°=180°.

易得∠1+∠3=180°.

又因为∠2+∠3=180°，

所以∠2=∠1，即∠BPD=∠BAC.

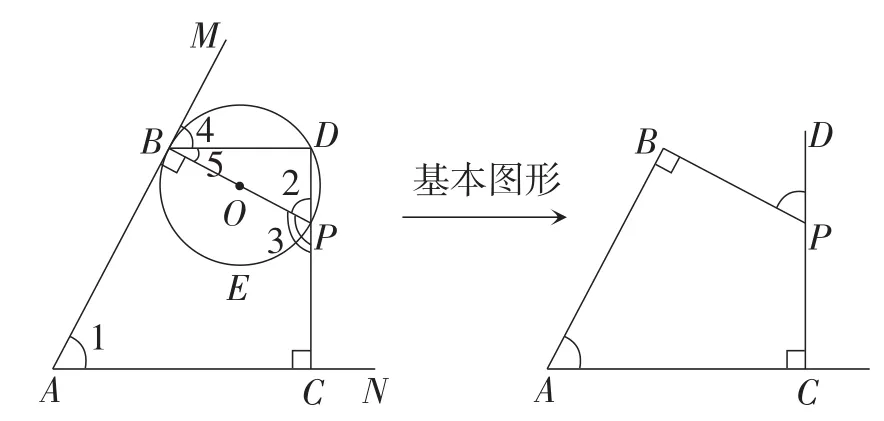
图2

解法2：如图2，因为PB为⊙O的直径，

所以∠BDP=90°，即∠2+∠5=90°.

由已知易得BD∥AC.所以∠1=∠4.

因为∠4+∠5=90°，

所以∠2=∠1，即∠BPD=∠BAC.

解法3：如图3，过点A作AK⊥DK，交DB的延长线于点K，

可得∠KAB=∠PBD，且∠KAB+∠BAC=90°.

因为∠PBD+∠DPB=90°，

所以∠BPD=∠BAC.

图3

解法4：如图4、图5，延长BP，交AC的延长线于点G，

易得△BDP∽△GCP∽△GBA.

可得∠BPD=∠GPC=∠BAC.

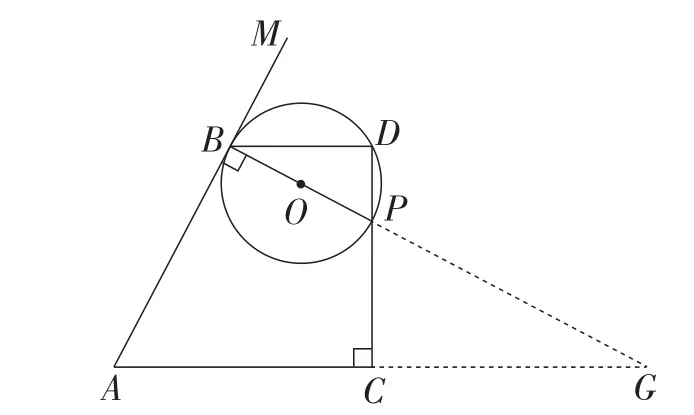
图4

图5

解法5：如图6，延长AB，CD，交于点H，方法同上，略.

图6

2.第（2）小题第①问思路探析

此问最关键的一步是利用“在同圆中，同弧所对的圆周角相等”得到△ABP为等腰直角三角形，然后利用勾股定理、相似三角形、三角函数建立方程.由已知条件，tan∠MAN=2，联想到遇到三角函数便构造直角，通过构造“三垂图”，架起已知与未知的联系.

解法1：如图7，因为 ∠BPE=∠BDE=45°， 且∠ABP=90°，

所以△ABP是等腰直角三角形.

由 tan∠BPD=tan∠MAN=2，

可设PD=x，则BD=2x.

在Rt△BDP中，由勾股定理得PD2+BD2=BP2，

解得x=2或x=-2（舍去），即PD的长为2.

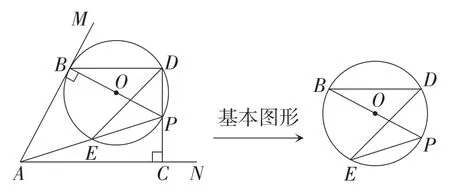
图7

解法2：如图7，同解法1，得.

在Rt△BDP中，由 tan∠BPD=2，

解法3：如图8，过点B作BI⊥AN，交AN于点I，

图8

解得x=2或x=-2（舍去），即PD的长为2.

3.第（2）小题第②问思路探析

此问延续2017年浙江温州中考试卷第24题的风格，在分类上难度降低了，消除学生不知如何分类、

易得△BAI∽△BPD.

由 tan∠BPD=tan∠MAN=2.

设PD=x，则CP=4-x，AC=2+2x.

在Rt△APC中，CP2+AC2=AP2，分不全的思维盲点，注重解法的多样化.每一类解法的思路形成需要学生心中有基本图形，能从复杂图形中透视出基本图形，从而找到各个量之间的联系.此问可以通过设元，用含未知数的代数式表示相关线段，并利用相似三角形性质、勾股定理等建立方程.

对每一种分类，笔者都给出了2种解法，其中每种分类的解法1通过等角转移，将△BED的三个内角转移到共顶点P的一个平角上，这个基本图形要在教学中加以内化.其中图8中的BP及图11中的AP充当着角平分线的角色，若能挖掘这层本质关系，问题将迎刃而解.每种分类的解法2凸显圆的轴对称性，巧妙地实现了各个量之间的关系，当然第三种分类中的解法2涉及半角模型的构建，以及后面分母有理化的过程，对学生来说存在一定的难度.

若△BED为等腰三角形，可以分如下三类进行分类讨论.

（1）当BD=BE时.

解法1：如图9，易得∠EPB=∠BPD，

即tan∠EPB=tan∠BPD=2.

在Rt△BPD中，由tan∠BPD=2，得BD=2.

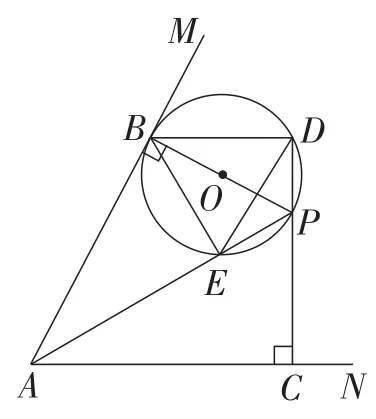
图9

解法2：如图9，由已知可得EP=DP，∠BEP=∠BDP=90°， ∠EPB=∠BPD.

在Rt△BEP中，因为BE=2，所以BD=BE=2.

（2）当DB=DE时.

解法1：如图10，易得∠DBE=∠DEB.

因为四边形BEPD是⊙O的内接四边形，

所以∠APC=∠DBE=∠DEB=∠BPD.

所以tan∠APC=tan∠BPD.

设DP=x，由，得.

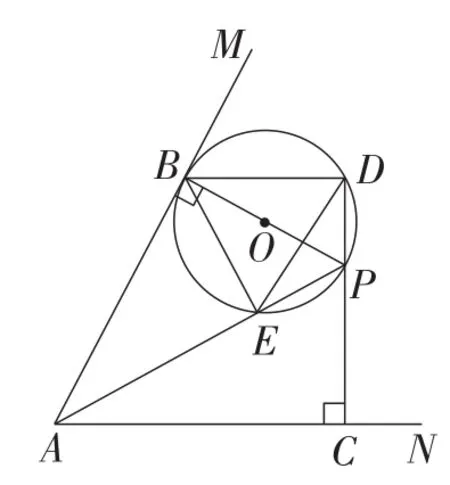
图10

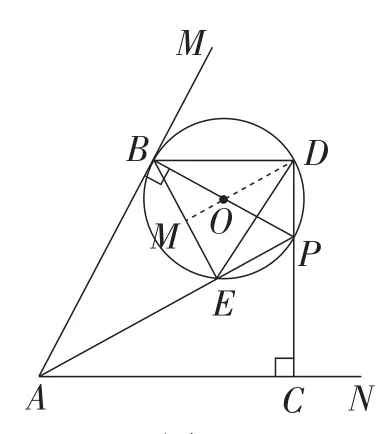
图11

解法2：如图11，连接DO并延长，交BE于点M，

则BM=EM，∠EBD=∠BED=∠BPD.

所以tan∠BED=tan∠DPB=2.

设PD=x，则DE=BD=2x.

由△BEP∽△ABP，得.

（3）当EB=ED时.

解法1：如图12，得∠APC=∠DBE=∠BDE=∠APB.

又由∠ABP=∠ACP=90°，得.

过点B作BH⊥AC，

在Rt△ABH中，由 tan∠MAN=2，，

得AH=2.

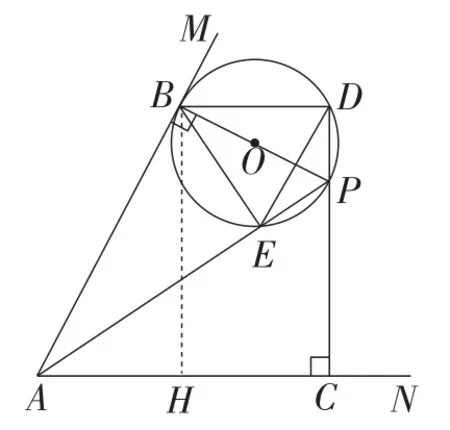
图12

图13

解法2：如图13，连接EO并延长，交BD于点N，

则DN=BN=PD，得.

又因为∠BPA=∠BDE，易得tan∠BAP=tan∠DEN.

综上所述，当BD为2或3或时，△BDE为等腰三角形.

4.第（3）小题思路探析

此小题涉及三角形的中位线，等腰三角形及相似三角形等核心知识，要善于挖掘基本图形，利用线段之间的关系求出面积的比值，如解法1、解法2.最后一小问，由于时间有限，有的学生通过猜想的方法加以解决，如解法3，很好地考查了学生直观想象的能力.

解法1：如图14，过点O作OQ⊥CD，交CD于点Q，

图14

由tan∠BPD=tan∠MAN=1，得BD=DP.

设PD=BD=2a，PC=b，

则AC=4a+b，OQ=PQ=a，CQ=a+b.

由OC∥BE，得∠OCH=∠PAC.

易得 Rt△ACP∽Rt△CQO.

所以AC·OQ=CP·CQ.

所以(4a+b)a=b(a+b).

可得2a=b.易得.

解法2：考虑到最后求比值，可以用特殊值法.

设CP=1，PD=BD=2a.其他同解法1，可得a=0.5.下同，略，这样可简化运算.

解法3：由 tan∠MAN=1，即 ∠MAN=45°，猜想45°的“12345”模型.这个证明留给读者思考.

四、结束语

笔者认为，对一道动态几何压轴题的研究，先要研究其解法，特别是要思考这种解法是如何想到的，在此基础上，进行教学思考.在教学中，一要重视引导学生挖掘题中隐藏的基本图形，此题就包含着很多常见的基本图形，如相似三角形；二要重视对数学思想方法的渗透，此题通过设元，用含未知数的代数式表示相关的线段，并建立方程，这种设元建立方程的思想非常重要.另外，题中还涉及到分类讨论、数形结合等思想方法；三要提倡问题解法的多样化，一题多解，开阔学生思路，发散学生思维，使学生学会多角度分析和解决问题.在解题教学中，当呈现一种解法后，教师可及时追问一句“还有其他解法吗？”学生由此展开不同思路的探究与交流；四要关注数学问题的本质内涵，现行中考试题加大了对数学问题本质的探究，弱化了对特殊技巧的考查，这需要教师在平时的解题教学中善于就问题进行分析、挖掘，寻找隐含在其中的本质内涵，才能有效地形成解题思路.