从“几何、代数、三角”三个维度揭密几何计算的思考策略
——基于一道中考几何计算题解法的分析与启示
李 明
(江西省赣州市第一中学)
著名数学家波利亚指出:拿一个有意义而又不复杂的题目去帮助学生挖掘问题的各个方面,使得通过这道题就好像通过一道门户,把学生引入一个完整的领域.几何计算是给出已知条件,让学生去推理计算,许多时候学生的思维盲目,难以想到解题切入点.以2017年重庆市中考试卷第18题(填空压轴题)为例,从“几何、代数、三角”三个不同维度探寻几何计算的思路,让学生感受几何计算的多种解法,把学生引入一个几何计算领域,提高学生解题能力和核心素养.
题目如图1,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若F是AB的中点,则△EMN的周长是____.

图1
一、解法初探
此题以正方形为背景,融入翻折变换、全等、相似,难度大,计算复杂,对学生的推理要求高.为帮助学生突破难点,笔者让学生先独立思考、探索、发现,思考根据题目条件,容易求出哪些线段的长度,能推出哪些结论?
经过探究,学生得出以下结论.
结论2:由△AGF∽△CGD,得,DG=
结论3:A,D,E,F四点共圆,且∠EFM=∠DFE=.
结论4:如图2,D,N,M,B四点共线,AC⊥DN,设AC与DM的交点为点O,则.
理由:如图2,连接MB,作GP⊥AB,MQ⊥AB,
易证得△GPF≌△FQM.
所以GP=FQ=AP,PF=QM.
因为AF=BF,所以PF=QB=QM.
所以∠QBM=∠ABD=45°.
所以D,N,M,B四点共线.所以AC⊥DN.

图2

图3
结论5:如图3,∠1=∠2=∠3=∠4.
理由:由A,D,E,F四点共圆,AC⊥DN容易推出.
二、妙解评析
在学生独立思考、探索的基础上,全班开展小组讨论,经过合作交流,学生涌现出许多奇思妙想,探究出了很多精彩的计算方法.
1.从相似三角形与勾股定理入手
思路1:计算线段长度常常考虑用“相似三角形中对应边成比例”连接已知线段和未知线段的关系.相似三角形有如图4~图8所示的5个常用的基本图形,笔者在教学中称它们为“五朵金花”.
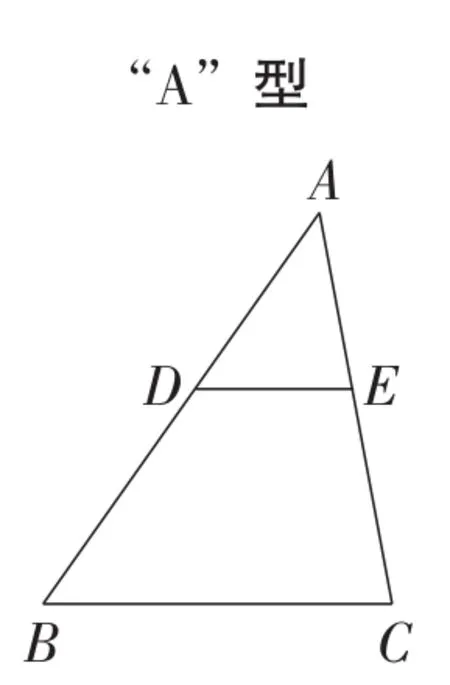
图4

图5
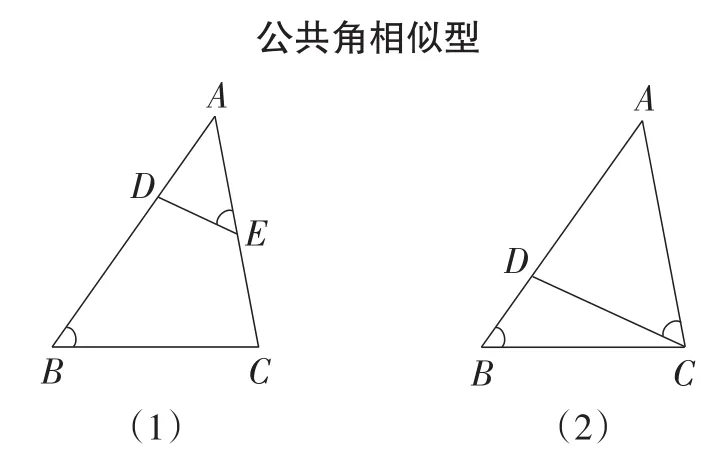
图6

图7

图8
在复杂图形中,寻找或通过辅助线构建相似基本图形是计算线段的常用思考策略.

图9
解法1:如图9,由题目条件,根据勾股定理易求出DF,AC,DE,EF的长.由△AGF∽△CGD(“X”型)易求出GF,DG,AG,CG的长.通过△AGF∽△DGE(“X”型)建立未知线段和所求出线段间的等量关系,求出线段EG(即EM)的长.连接MG,MG∥DE,得出△FGH∽△FDE(“A”型),△DEN∽△MHN(“X”型),得问题转化为求线段EH,DN的长,,从而求出线段EN,MN的长.
【评析】此题要求的线段和已知条件没有直接联系,为此,抓住图中的4对相似三角形(△AGF∽△CGD,△AGF∽△DGE,△FGH∽△FDE,△DEN∽△MHN)构建线段间的等量关系,通过相似,架起沟通已知和未知的桥梁.解法1较为复杂,后3对相似三角形学生难以想到,但可以让学生充分感受“相似法”在计算线段长度中的威力.
解法2:如图10,在Rt△DEN中,EO⊥DN,易联想到“母子相似形”△DOE∽△EON∽△DEN,根据OD,DE的长可以求出OE,ON,EN,DN的长.

图10
由EM=EG=OE+OG=OE+(OA-AG),求出EM的长.由,求出MN的长,得.
【评析】由四边形对角互补想到四点共圆是常用的解题策略,利用圆的性质更容易发现题目中角之间的等量关系.由翻折得∠GFM=90°,通过添加辅助线构造“三等角相似形”证出D,N,M,B四点共线(祥见解法初探),进而发现OE⊥DN,OD=OA.在“母子相似形”中知任意两条线段的长可求出其余所有线段的长,在直角三角形中运用勾股定理计算线段长度也是最常用的方法,本解法让学生感受“母子相似形”在计算线段长度中的应用.
解法3:同解法2求出EN,EM的长.如图10,由△MEN∽△MDE,可得求出MN的长,得.
【评析】解法1中求MN的长思考难度大,解法2中求MN的长计算量大,交流中学生又发现了△MEN∽△MDE(公共角型),且相似比为1∶2,从而MN=,轻松求出MN的长.
反思上述三种解法,在复杂图形中寻找或构建相似三角形(上面用到了相似三角形的5个基本图形),通过相似三角形得到线段间的比例关系,完成从已知向未知的过渡.在几何计算中,“相似”好比一盏亮着的灯,利用相似得到相等关系是一个重要的解题思路.在复杂图形的分析中,若能把图形分解为简单的相似基本图形,解题思路便会豁然开朗.
2.从“面积比与线段比的互相转化”入手
思路2:解题中为了寻找线段间的数量关系,还可以从图形的面积入手.在面积比与线段比的相互转化中,有两种常用思考策略:一是相似三角形的面积比等于相似比的平方;二是等高三角形的面积比等于底的比,或等底三角形的面积比等于高的比.
解法4:同上求出DN,EN,EM的长.

图11
如图11,连接GN,由FG∶GD=1∶2,求出S△NFG∶S△NGD=1∶2. 由△NGF≌△NMF,得S△FMN∶S△FND=1∶3.进而得MN∶DN=1∶3.由此求出MN的长,得C△EMN=EN+.
3.从全等三角形与整体思想入手
思路3:利用全等三角形实现线段间的等量转化,把求三边和作为一个整体来计算,使运算更为简便.
解法5:同解法2,求得.
如图12,作EH⊥DF于点H,交DN于点K.由 △EKD≌△FME, 得EM=DK,FM=EK.由 △EKN≌△FMN,得MN=KN.所以C△EMN=EN+NM+EM=EN+NK+DK=EN+.

图12
【评析】在前面4种解法中,学生利用相似三角形、勾股定理、面积等知识分别求出三角形的三边长,从而求出周长.在交流中,学生思维活跃,有学生运用整体思想想到把三边的和作为一个整体计算.学生在探究中抓住等腰直角三角形DEF,作底边上的高EH,证出两对全等三角形△EKD≌△FME,△EKN≌△FMN,从而EM+MN=DK+KN=DN,△EMN的周长转化成EN+DN的长,使问题得以解决.在等腰三角形中,作底边上的高是添加辅助线常用的方法.课堂上,教师若给学生留下思考的时间和空间,学生往往会给你带来意外的惊喜.
4.从锐角三角函数与解直角三角形入手
思路4:在直角三角形中,知道一边和一个锐角的三角函数值,可以求出该三角形的另外两边长,把要求线段放在直角三角形中计算.

图13
解法6:如图13,连接GM,交EF于点H,在 Rt△DAF中,易求,由tan∠4=,可求出EN的长.在Rt△EHM和Rt△NHM中, 由 tan∠2=tan∠5=,得NH∶MH∶EH=1∶2∶4,则,可求得HN的长,利用勾股定理或比值关系可求出MN,EM的长.
【评析】在解题教学中,笔者经常向学生提起“相似”和“三角”是一对好朋友,“相似”和“三角”都和比值相关,运用“三角法”解题往往更为简便.解法6通篇没有用相似,而是巧妙利用三角函数建立已知线段和未知线段的等量关系,抓住tan∠4=tan∠2=与勾股定理,轻松求出了所求线段的长,让学生领略了“三角法”在计算中的神奇表现.
5.从直角坐标系入手
思路5:要求出三角形三边的长,从代数角度考虑,可以建立平面直角坐标系,求出线段端点坐标,从而利用两点间距离公式或勾股定理求出线段长.
解法7:如图14,建立平面直角坐标系,易得D(0,4),C(4,4),H(2,2),F(2,0).
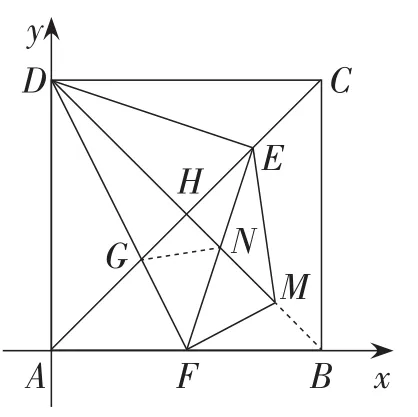
图14
由待定系数法求出直线AC,DF,DB的解析式,求得直线AC与DF的交点G的坐标.由ED=EF,列方程可求得点E的坐标.求出直线EF的解析式,与直线DB的解析式联立求出点N的坐标.根据两点间距离公式求得EG,EN,NG的长.
【评析】坐标法是通过代数计算来完成几何证明或计算的一种解题方法.此题要计算三角形的周长,容易想到只需要确定三角形三个顶点的坐标,问题便得以解决,相比前面相似法、全等法、面积法、三角法,思维难度大大降低.在解答时,注意把求E,N,M三点的坐标转化为求E,N,G三点的坐标,可以有效减小计算量.坐标法的学习让学生体会代数与几何的密切联系,可以培养学生的数形结合能力,为学生高中学习解析几何奠定基础.
三、教学启示
回顾此题的教学,在解法初探中教师提出一个开放性的问题,让学生从条件出发,去探究能得出哪些正确结论,这是思考问题的常用方法.学生从题中已知的一条线段长出发,求出了一系列线段的长,并探究出了四点共圆、四点共线,为解决问题奠定了坚实的基础.综观上述5种思路、7种解法,学生从相似、面积、全等、三角、坐标等不同角度探究计算思路,搭建从已知通向未知的桥梁,训练学生从不同角度思考问题的能力,促使学生从单一的思维模式中解放出来,以创新思维、求异思维的方式来解决问题,较好地培养了学生思维的严密性、开阔性、发散性和灵活性.
一个令许多学生望而生畏的几何计算填空压轴题,课堂上学生精彩解法的展示令教师和全班学生惊叹不已.在这道题的解法探究中,初中数学计算线段长度的常用方法在这道题中得到了淋漓尽致的呈现.学生通过反思总结,感受了几何线段计算领域常用到的思想方法,如勾股定理法、面积法、全等法、相似法、三角法、坐标法等.透过每种解法的表层,抓住每种解法的本质,把握不同解法之间的联系,能让学生触类旁通、举一反三,有望达到“做一题,通一类,会一片”的较高层次效果.
解题教学的最终目标是发展学生的思维,科学精神、理性思维是核心素养的重要成分.通过一题多解,引发学生反思几何计算与几何推理之间的内在关系,发展学生的思维能力,让学科核心素养的培育落实到具体的数学教学中.

