变式教学不深奥 灵活多变皆有道

宋柏锋

（辽宁省大连市第三十七中学）

变式教学是教师通过不断变换问题中的条件或结论，转换问题的内容和形式，更换问题中的非本质特征，促进学生掌握数学对象本质属性的一种教学方法.变式教学对增强学生思维的深刻性，提高学生数学学习的积极性，提升学生的创新意识等都有着积极的作用.笔者通过对人教版《义务教育教科书·数学》八年级下册“勾股定理”一章中一道典型题目的变式研究，与各位同行分享对变式教学的一些思考.

一、原题解析

题目如图1，P是等边三角形ABC内的一点，∠BPC=150°，求线段PA PB，PC之间的数量关系.

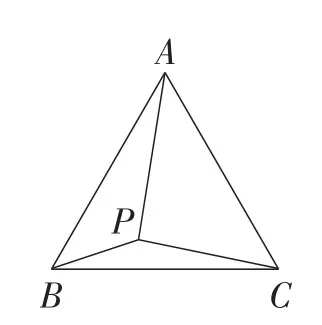
图1

1.解题思路

依托AB=AC=BC，分别按如图2～图7所示旋转，将PA，PB，PC转化至一个三角形，再通过已知角度，证明转化后的三角形为直角三角形，进而得到PA2=PB2+PC2.

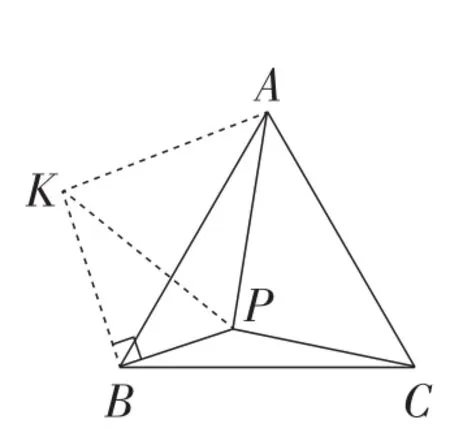
图2

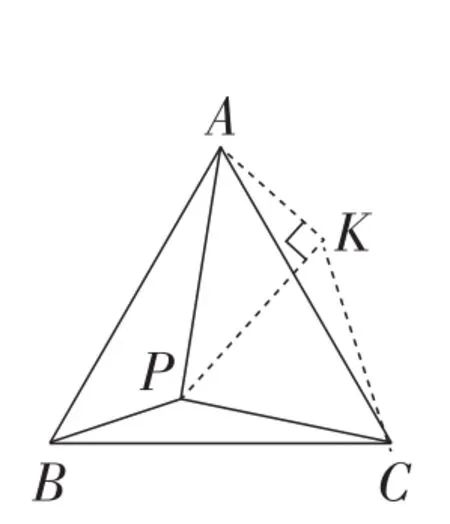
图3

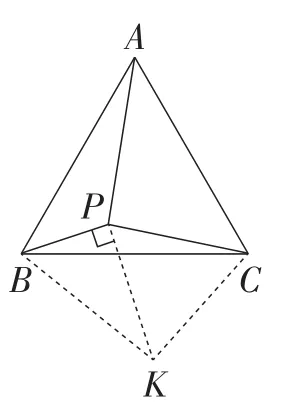
图4

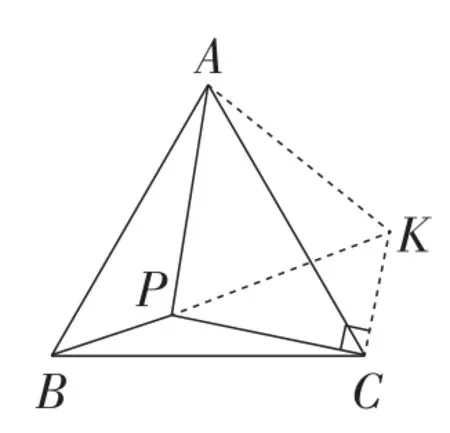
图5

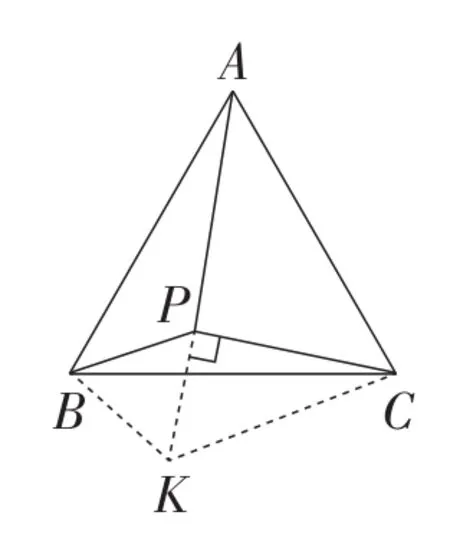
图6

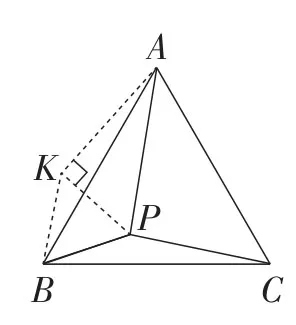
图7

以图2为例进行证明.

解：如图2，过点A作∠KAP=∠BAC，在AK上截取AK=AP，连接BK，PK.

因为△ABC为等边三角形，

所以BA=CA，∠ABC=∠BAC=60°.

所以∠KAB=∠KAP-∠BAP=∠BAC-∠BAP=∠CAP，∠KAP=60°.

所以△KBA≌△PCA，△AKP为等边三角形.

所以KB=PC，∠AKB=∠APC，KP=PA.

因为∠BPC=150°，

所以∠KBP+∠KAP=360°-（∠AKB+∠APB）=360°-（∠APC+∠APB）=∠BPC=150°.得∠KBP=90°.

所以KB2+BP2=KP2，即PA2=PB2+PC2.

2.教学关注点

（1）提倡一题多解，这样有利于学生在多解中体会原题线段转化的本质.

（2）提倡从构造全等、旋转，构造90°等多角度分析思考问题.

（3）严格规范过程书写，对于辅助线作法等易错过程进行纠正.

3.解法中的变与不变

变：辅助线的作法及思考问题的切入角度.

不变：利用几何变换将三条线段转化到一个直角三角形中，进而得到三边关系的解题策略及转化的思想方法.

二、原题变式

变式系列1：变化问题载体，弱化条件

变式1：如图8，P是正方形ABCD内一点，∠BPC=135°，求线段PA，PB，PC之间的等量关系.

变式2：如图9，P是菱形ABCD内的一点，∠ABC=120°，∠BPC=120°，求线段PA，PB，PC之间的等量关系.

变式3：如图10，P是菱形ABCD内一点，∠ABC=α，∠BPC=β，当α与β之间满足怎样的关系时，PA2=.

图8

图9

图10

以变式3的解法为例，解法如下.

解析：如图11，过点B作∠PBK=∠ABC=α，在射线BK上截取线段BK=BP，连接PK，CK，过点B作BE⊥PK于点E，

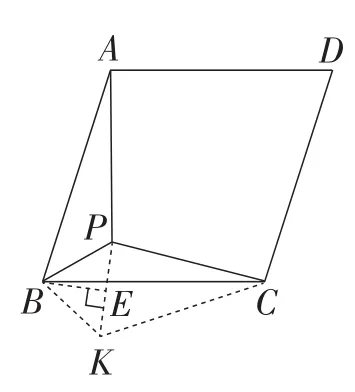
图11

因为BA=BC，∠PBK=∠ABC=α，

所以∠ABP=∠ABC-∠PBC=∠PBK-∠PBC=∠CBK.

所以△ABP≌△CKB.所以PA=CK.

所以CK2=PK2+PC2.

所以 ∠KPC=90°.

因为∠BPC=∠KPC+∠BPK，

所以α+2β=360°.

（1）教学关注点.

变式系列1为原题条件的变化与弱化，变化过程中，不变的是当BA=BC时，当∠ABC和∠BPC满足一定度数时，PA，PB，PC之间存在类似勾股定理的结论.教师在教学过程中应注意以下几点.

①让学生通过自主学习、小组交流等学习方式，感受因条件变化而减少的辅助线作法.原题目以点A，B，C为旋转中心皆可解决问题，而变式系列1只能以点B为旋转中心.因为以点A，C，D为旋转中心无法将PA，PB，PC转化到一个三角形中，教学时应与学生共同探索并发现此变化.

②让学生经历在条件弱化的过程中得出一般性的结论.

③变式3的设计意图是为了保证问题设置的连贯性，让学生经历由特殊到一般的过程，因部分内容涉及九年级锐角三角函数的内容，在教学中可根据学情酌情选择.

（2）此题中的变与不变.

变：数学问题的载体在不断发生改变.

不变：①当BA=BC，∠ABC和∠BPC满足一定关系时，PA，PB，PC之间便存在某种数量关系.

②通过全等、等腰等几何变换，将三边转化到一个三角形中的转化思想未发生改变.

③依托点B（已知角度的顶角、已知等腰的顶点）作辅助线的策略未发生改变.

变式系列2：变化图形中核心元素的相对位置关系

变式1：如图12，P是正方形ABCD外的一点，线段PA，PB，PC之间满足PA2=2PB2+PC2，求∠BPC的度数？

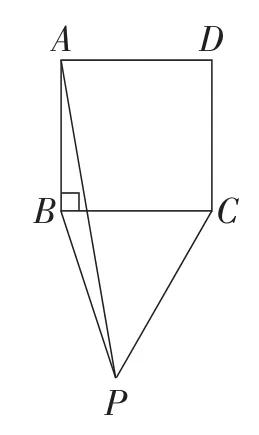
图12

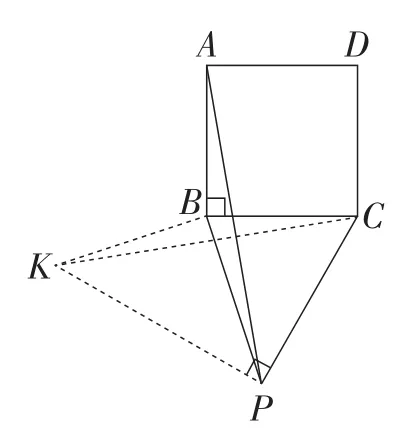
图13

解析：如图13，依托BA=BC，将△ABP绕着点B顺时针旋转90°至△BKC，连接KP，得PB=KB，AP=KC，最终将PA，PB，PC转化到△KPC中.因为PA2=2PB2+PC2可以得出∠CPK=90°，继而得出∠BPC的度数为45°.

变式2：如图14，P是正方形ABCD外的一点，线段PA，PB，PC之间满足PC2=2PB2+PA2，求∠BPA的度数？

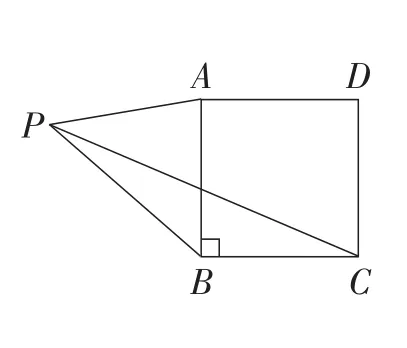
图14

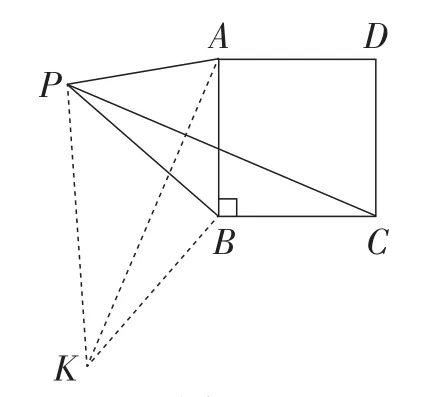
图15

解析：如图15，将△PBC绕点B逆时针旋转90°至△ABK，连接AK，PK，得BK=BP.思路与上题相同，此外，可以引导学生从轴对称图形的角度思考问题，快速得出结论.

变式3：如图16，P是正方形ABCD对角线AC上的一点，求线段PA，PB，PC之间的数量关系？

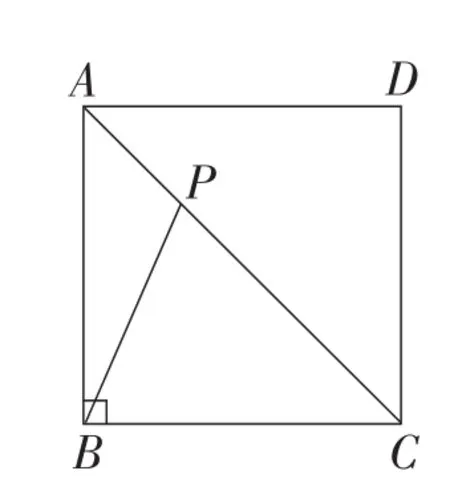
图16

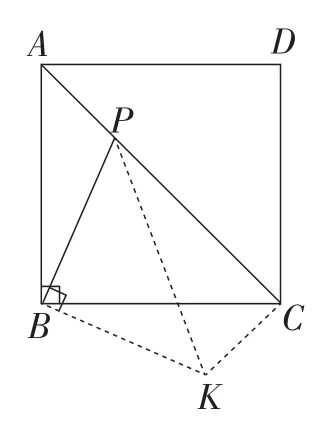
图17

解析：如图17，过点B作∠KBP=∠ABC，在BK上截取BK=BP，连接CK，PK.此题点P处于特殊位置，可以将△APB旋转至△BKC的位置，因为∠BAC=∠ACB=45°，所以∠PCK=90°.所以PK2=CK2+PC2.进而得2PB2=PA2+PC2.

此题在教学中可继续变式（如图18），利用2PB2=PA2+PC2的不变性变式如下.

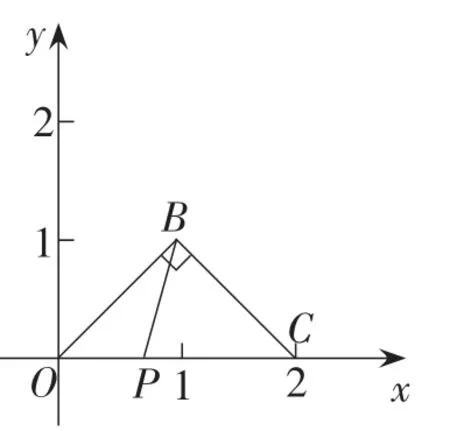
图18

变式4：如图18，在平面直角坐标系中，已知B(1，1)，C(2，0)，P为线段OC上一点，，求线段PC的长度.

解析：由B(1，1)，C(2，0)，可得△OBC为等腰直角三角形.由变式系列2中变式3的结论可得2PB2=PO2+PC2.又因为，所以设OP=x，所以4x2=x2+(2-x)2.进而得出.

此题是将条件与结论进行数形转化变式.

（1）教学关注点.

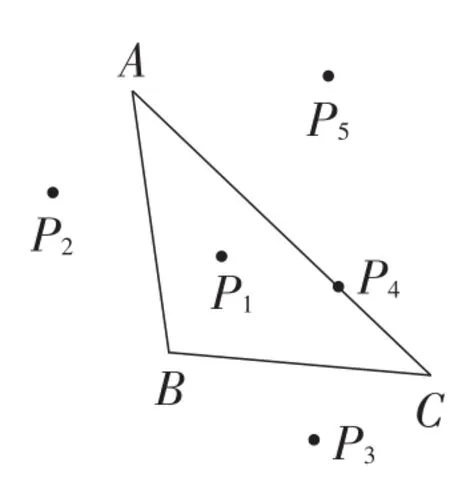
图19

变式系列2本质上是在等腰三角形ABC中，点P分别位于点P1，P2，P3，P4，P5等位置 （如图19），连接PA，PB，PC，当PA，PB，PC满足类似勾股定理的结论时，∠ABC与以点P为顶点的最大角之间的存在着某种特定的数量关系.在教学过程中，教师应根据学情选取适当的变式题目，让学生在变化中感受不变的核心，进而类比解决问题，依托题目变式，感受类比转化思想，提升解题能力.

（2）此题中的变与不变.

变：问题提问的方式；问题中几何元素间的相对位置.

不变：变式系列1中不变的内容仍未发生改变；从旋转的角度思考问题的技巧在此系列变式中显得尤为重要.

三、关于变式教学的几点思考

1.变式教学贵在不变

上述7个变式先后改变了问题的解法、题设和结论等，但研究问题的方式、方法及策略始终未变.多元智能理论的主要创建者加德纳认为，课堂上学生对于知识真正的理解来自对少数主题深入的研讨，而不是对许多内容的广泛讨论.“少”就是我们要抓住的不变的本质，抓住“少”才能衍生出“多”，通过对“少”的多层次的变式构造，不但可以使学生对问题解决过程及问题本质的结构有一个清晰的认识，而且也能有效地帮助学生积累问题解决的经验，并提高解决其他问题的能力.

2.变式教学贵在有道

变式教学贵在变之有道，即变化应遵循数学知识发生、发展的逻辑链条，体现学生认知链的合理延伸.变式教学不是针对某一知识点的同水平的数学问题的反复操练与训练，因为简单的讲授与模仿不能帮助学生进入高思维含量层面的学习与积累，反而会使学生的思维僵化并产生惰性.以本文的变式为例，每次变化都不是简单的重复与罗列，而是要通过问题的多种呈现帮助学生寻找变化中隐藏的不变的本质.

3.变式教学贵在创新

爱因斯坦有句名言：提出一个问题往往比解决一个问题更重要.解决问题是被动完成任务，而提出问题是主动思考和创新思维.变式教学表面是教师在设计变式题目，学生在被动学，但在深层次上，学生在抓住问题本质的同时学会了从多角度思考问题的方式，也为学生提出问题提供了切实可行的渠道.本文就为学生提供了变换问题载体、弱化题目条件、改变几何元素之间的相对位置关系等变式方法，对几何题目进行变式思考的具体渠道.