解题利器——椭圆中有关中点弦的性质

■浙江省海宁中学

利用椭圆中点弦的性质,可以快捷、方便地解决有关中点弦问题。

一、利用椭圆中点弦的性质，解决有关中点弦的斜率、所在直线方程问题

例1已知椭圆=1内有一点P(3,1),过点P的直线l与椭圆交于A、B两点。若弦AB的中点恰为点P,则该直线l的斜率为 。

分析:椭圆方程确定,中点确定,可以利用上述中点弦性质,得到所需的结论。

例2已知椭圆内一点P(-1,1),过点P的直线l与椭圆交于A、B两点。若弦AB的中点恰为点P,则该直线l的方程为 。

分析:要求直线方程,已知其过点P,则根据点斜式只需知道该直线的斜率即可。

解:由题意知,a2=9,b2=4,kOP=-1,所以此,该直线l的方程为),整理得4x-9y+13=0。

点评:本题通常采用的方法是点差法或设定直线方程,然后与椭圆方程联立,利用韦达定理及中点坐标公式,建立与斜率有关的方程,通过解方程来获取所求直线的斜率。与上述利用性质解决问题相比,常法就显得相对比较烦琐。故若有性质、结论可以直接使用,不妨一试。

二、根据椭圆中点弦的性质，求有关椭圆方程

例3已知过点P(3,2)且斜率为-2的直线l与椭圆交于A、B两点,若弦AB的中点恰为点P,则实数m的值为 。

分析:直线方程的斜率和中点确定,则可以直接利用性质得到实数m的值。

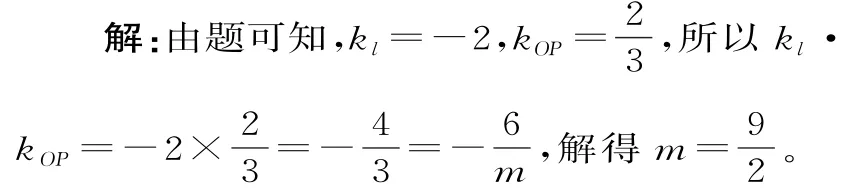
点评:应用中点弦性质时,不需要关注椭圆焦点的位置。该性质可以改写为:过椭圆内一点P作直线交椭圆于A、B两点,若点P为弦AB的中点,则

三、根据椭圆中点弦的性质，探求椭圆方程中系数的比例关系及离心率问题

例4已知椭圆mx2+ny2=1(m,n＞0,m≠n)与直线y=1-x交于M、N两点,过原点与线段MN中点所在直线的斜率为的值为 。

四、利用椭圆中点弦的性质，探求中点坐标、轨迹问题

(1)求椭圆C的方程;

例7已知椭圆与一组斜率为2的平行直线相交,探究这组直线被椭圆截得的线段的中点是否在同一条直线上。若是,求出该直线方程;若不是,请说明理由。

分析:由条件可知,假设该直线过坐标原点,则由椭圆的对称性知中点恰为原点。要判断所得弦的中点是否在同一直线上,则只需判断这些中点与原点的连线的斜率是否相同即可,由此可以利用中点弦性质判断。

解:由题意可设直线与椭圆相交所得弦的中点为P,则由中点弦性质可知k·kOP=因为k=2,所以,即无论该组平行直线如何变化,其中点与原点的连线斜率保持不变。故这组直线被椭圆截得的线段的中点在斜率为且经过坐标原点的直线上,该直线方程为,即x+6y=0。

点评:利用椭圆中点弦的性质,可以免去我们联立方程,利用韦达定理及中点公式来进行计算的烦琐,还可以简化我们的运算过程。

中点弦问题是椭圆中一类比较特殊的问题,我们可以采用常规的方法联立直线与椭圆方程,利用韦达定理及中点坐标公式解决相关问题,也可以根据其特殊性,利用点差法,采用设而不求的方式,结合两点求斜率公式进行表示。当然,如果我们能够看到中点弦这一结论性公式,并能够作简单的应用的话,对于我们的运算,将起到大大简化的作用,同时也能够提高运算的准确性。这一中点弦性质不仅仅在椭圆中可以应用,在后续的双曲线问题中,也有类似的中点弦的结论性公式,同学们在学习了这一公式后,不妨在后续的双曲线学习中自行对该性质作简单的推导并应用。