广义S-型模李超代数的生成元
董艳芹,金明浩,王 颂,张永正
(1.长春师范大学数学学院,吉林 长春 130032;2.吉林省实验中学,吉林 长春 130022;3.东北师范大学数学与统计学院,吉林 长春 130024)
1 广义S-型模李超代数的构造

令q∈N,r=n+q.Λ(q)表示域F上具有q个未定元xn+1,xn+2,…,xr的外代数.定义
B(q)∶={〈i1,i2,…,ik〉|n+1≤i1 若{u}={i1,i2,…,ik}∈B(q),则令|u|=k,xu=xi1,xi2,…,xik.约定|∅|=0,x∅=1.则{xu|u∈B(q)}构成了Λ(q)的一个F-基底. 设D1,D2,…,Ds是A上的线性变换,且满足 则D1,D2,…,Ds是A的超导子.容易看出对任意i∈I2,Di(x(α)xuyλ)=λix(α)xuyλ.令 [fDi,ɡDj]=fDi(ɡ)Dj-(-1)P(fDi)P(ɡDj)ɡDj(f)Di, (1) 其中f,ɡ∈A,i,j∈J.令 其中 令 因此引理成立. 引理2.2Dij(xπ)∈X,i,j∈I0. 证明为了证明这个结果,对t用归纳法来证明Dt-1t(x(π1ε1+…+πtεt))∈X,其中t∈I0.先考察t=2的情况.设k,l∈I1,k≠l,则有 D12(x(2ε1)xk)=[D12(x(3ε1)),Dl1(xkxl)]∈X, D1k(x((π1-1)ε1)xk)=-[D1k(x(π1ε1)),D1l(xlxk)]∈X, D12(x(π1ε1)xk)=[D12(x(2ε1)xk),D1k(x((π1-1)ε1)xk)]∈X, D2k(x((π1-1)ε1+(π2-1)ε2)xk)=-[D12(x(π1ε1)xk),Dk2(x(π2ε2))]∈X, D2k(x(2ε2)xk)=-[D2k(x(3ε2)),D2l(xlxk)]∈X, D2k(x((π1-1)ε1+π2ε2)xk)=-1/2[D2k(x((π1-1)ε1+(π2-1)ε2)xk),D2k(x(2ε2)xk)]∈X. (2) 同理有 D1k(x(π1ε1+(π2-1)ε2)xk)∈X. (3) 此外, D12(x(2ε2+ε1))=-[D12(x(3ε2)),D12(x(2ε1))]∈X, D12(x(π1ε1+ε2))=-[D12(x(π1ε1)),D12(x(2ε2+ε1))]∈X, Dk2(x(ε2)xk)=[Dk2(x(2ε2)),D2l(xlxk)]∈X, Dk1(x((π2-1)ε2)xk)=-[D12(x(π2ε2)),Dk2(x(ε2)xk)]+D12(x(π2ε2))∈X, D12(x((π1-1)ε1+π2ε2))=[D12(x(π1ε1+ε2)),Dk1(x((π2-1)ε2)xk)]∈X, (4) D1k(x(2ε1)xk)=[D1k(x(3ε1)),D1l(xlxk)]∈X. (5) 由(2)—(5)式可得 D12(x(π1ε1+π2ε2))=-D21(x(π1ε1+π2ε2))= 故t=2时结论成立. 假设t时结论成立,即Dt-1t(x(π1ε1+…+πtεt))∈X.令t+1∈I0.因为 Dt-1 t(x(πt+1εt+1+εt))=-[Dt-1 t+1(x(πt+1εt+1)),Dt t+1(x(2εt+1+εt))]∈X, 故 Dt-1 t(x(δ-εt-1+πt+1εt+1))=[Dt-1 t(x(δ)),Dt-1 t(x(πt+1εt+1+εt))]∈X. 于是 Dt t+1(x(δ+πt+1εt+1))=[Di-1 i(x(xδ-εi-1+πi+1εi+1)),Di-1 i+1(x(3εi-1))]∈X. 即t+1时结论成立,归纳法完成.故Dn-1 n(x(π))∈X.设σ是{1,2,…,n}的任一个置换,同理知 Dσ(n-1)σ(n)(x(πσ(1)εσ(1)+…+πσ(n)εσ(n)))∈X. 显然πσ(1)εσ(1)+…+πσ(n)εσ(n)=π,从而Dij(x(π))∈X,∀i,j∈I0. 引理2.3Dij(x(π)xω)∈X,i,j∈J. 证明先来证明i∈I1,j∈I0时,Dij(x(π)xω)∈X. 首先用归纳法证明i∈I1,j∈I0,t∈I1时,Dij(x(π)xn+1xn+2…xt)∈X. 任取k∈I1{i},j′∈I0{j},则有 Dij′(x(2εj′)xk)=[Dij′(x(3εj′)),Dj′j(xkxj)]∈X. 由引理2.2知 Dij(x(π)xk)=-[Dj′j(x(π)),Dij′(x(2εj′)xk)]∈X. 从而 Dik(x(π)xk)=[Dij(x(π)xk),Dkj(x(2εj))]∈X, Dij(x(π)xn+1)=[Dik(x(π)xk),Djk(xn+1xk)]∈X. 假设t时结论成立,往证t+1∈I1时结论成立. 取l∈I1{t+1},则 Dj′j(x(2εj)xt+1)=[Djj′(x(3εj)),Dlj(xlxt+1)]∈X, Djj′(xjxj′xt+1)=-[Dlj(xj′xl),Dj′j(x(2εj)xt+1)]∈X. 由归纳假设知 Dij(x(π)xn+1xn+2…xtxt+1)=-[Dij(x(π)xn+1xn+2…xt),Djj′(xjxj′xt+1)]∈X. 由此可得i∈I1,j∈I0时,Dij(x(π)xω)∈X.类似可验证其他情况成立. 引理2.4Dij(x(π)xωyλ)∈X,∀i,j∈J. 证明为了证明Dij(x(π)xωyλ)∈X,∀i,j∈J.分下面几种情况讨论: Djl(xlxr′yλ)=[Dr′l(xlxr′yλ),Djl(xlxr′)]∈X. 进而由引理2.3, Dij(x(π)xωyλ)=(-1)p(xω)[Dr′i(x(π)xω),Djl(xlxr′yλ)]∈X. (2) 设i∈I1,j∈I2.任取l∈I0,r′∈I1{i},则有Dij(x(π)xωyλ)=[Dr′i(x(π)xω),Djl(xlxr′yλ)]∈X. (3) 设i∈I2,j∈I2.任取l∈I0,r′∈I1,则有Dij(x(π)xωyλ)=-[Dr′i(x(π)xω),Djl(xlxr′yλ)]∈X. 同理可证当i∈I0,j∈I0,i∈I0,j∈I1,i∈I1,j∈I1时,Dij(x(π)xωyλ)∈X.综上所述,对任意i,j∈J,有Dij(x(π)xωyλ)∈X. 令 M1∶={Dij(x(kεj))|i∈I,j∈I0,0≤k≤πj}, M2∶={Dij(xkxl)|i∈I,j∈I2,k,l∈I}, 则有下面结论成立: Dij(x(α)xuyλ)=[Dk,Dij(x(α+εk)xuyλ)]∈X.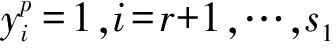

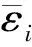
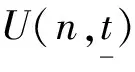

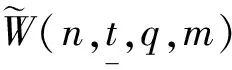

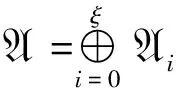
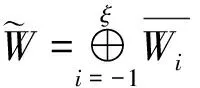
2 广义S-型模李超代数的生成元


-[D12(x((π1-1)ε1+π2ε2)),D1k(x(2ε1))xk]+D1k(x(π1ε1+(π2-1)ε2)xk)-2D2k(x((π1-1)ε1+π2ε2)xk)∈X.





