基于新四维混沌系统的复杂网络的混沌保密通信及噪声研究

付宏睿，董永刚，张建刚

(1.安阳学院建筑工程学院，河南 安阳 455000；2.兰州交通大学数理学院，甘肃 兰州 730070)

0 引言

气象学家Lorenz于1963年首次发现了一个三维自治系统中的混沌吸引子，从此混沌得到很快地发展，并在此基础上构造出许多新的三维混沌系统.[1-3]然而三维自治混沌系统的带宽比较窄，应用在保密通信中效果差，信号容易被破译.但是四维超混沌系统动力学行为更复杂，它具有2个或2个以上的正Lyapunov指数，因此更难预测.将其应用在保密通信中将会大大提高信号传输的保密程度.

近年来，许多学者将混沌系统与复杂网络结合在一起，将其表示为网络的节点，则复杂网络的同步就成为各个节点间的混沌同步问题[4-6].文献[7]研究了非线性耦合网络的时空混沌同步；文献[8]研究了复杂网络中具有相同结构节点之间的脉冲同步等；文献[9]研究了复杂动力网络的各个单变量之间相互替换耦合的同步；文献[10]基于Lyapunov稳定性理论，研究了一类分数阶复杂网络混沌系统的有限时间混沌同步.已有文献大部分都是对三维混沌系统的研究，很少将四维混沌系统应用到复杂网络的同步中，并且主要都是对复杂网络同步的理论研究，很少有对复杂网络同步的应用.本文在提出一个新四维混沌系统的基础上将其与复杂网络相结合，由于该系统动力学行为的复杂性，因此非常有利于应用到保密通信中.

目前，许多研究都利用混沌信号带宽频谱的非周期性以及对初值的敏感性和具有非常好的隐蔽性等将其应用到保密通中.[11-13]以往都是对信号只实施一次加密，而本文提出一种新的混沌保密通信系统，将有用信息经过多次加密，可以大大提高信息传输的保密程度.但是在现实中信息传输总会受到噪声的干扰，使有用信号发生畸变.因此，本文在保密通信的基础上加入了高斯白噪声[14-15]，使其对信号传输进行干扰，最后用小波变换原理对噪声进行处理[16]，从Matlab数值仿真来看，有用信号可以被无失真地恢复出来.

1 数学模型

1.1 模型提出

选取一个新四维自治混沌系统，该系统的状态方程为

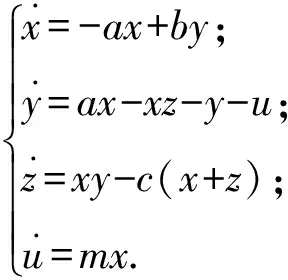
(1)

其中：x=(x，y，z，u)T∈R4为系统的状态变量；a，b，c，m∈R为系统的参数.运用Wolf算法可以计算出该系统的Lyapunov指数λ1=0.337 1，λ2=0.218 4，λ3=0，λ4=-26.436 1，并且该系统的Lyapunov维数DKY=3.020 65，则说明系统(1)处于超混沌状态.

1.2 系统(1)的平衡点与稳定性

特征方程为(λ+5)(λ3+21λ2-680λ+140)=0，则特征根依次为λ1=-5，λ2=-38.68，λ3=0.207，λ4=17.468 5.因此它的平衡点不是稳定的鞍点，说明系统(1)存在超混沌现象.

1.3 系统(1)的耗散性与吸引子的存在

1.4 系统(1)吸引子的数值仿真

图1 系统在不同空间的吸引子

2 基于系统(1)的复杂网络的同步

选取由N个相同节点通过耦合而构成的全局耦合网络，其中第i个节点的n维动力系统的状态方程为

(2)

将系统(1)表示为网络的各个节点，取节点数N=4，那么由该系统组成的4个节点的全局耦合网络模型为：

(3)

(4)

(5)

(6)

运用Matlab进行数值仿真，由运行结果可以看出：当耦合函数d=2时，尽管系统的初始状态不同，但还是可以较快地达到同步.图2为系统(3)—(6)的同步误差图，其中：图2(a)为节点1与节点2之间的误差；图2(b)为节点2与节点3之间的误差；图2(c)为节点3与节点4之间的误差；图2(d)为节点4与节点1之间的误差.

图2 系统(3)—(6)的同步误差图

3 基于复杂网络的混沌保密通信

3.1 保密通信方案

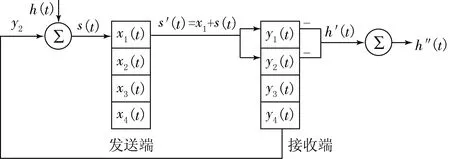
图3 混沌保密通信系统

为了提高网络中信息传输的安全性，提出了一种基于复杂网络新的混沌保密通信系统(见图3).该系统由结构复杂的四维超混沌系统组成，它的每个节点的动力学行为会更复杂，并且具有2个或2个以上的正Lyapunov指数.因此它的动力学特性非常有利于混沌保密通信的加密，其混沌信号对初值极端敏感，并且在接收端有用信号必须经过两次解调才能被恢复出来，所以该系统的保密程度比较高.

3.2 噪声干扰下信号的传输与小波去噪

为了分析信道中噪声对信息传输的干扰以及对信息解密时的影响，本文将5 dB的高斯白噪声干扰信号加入了信息传输与加密、解密的整个过程中(见图4).

图5 小波阈值去噪原理

小波阈值去噪原理如图5所示[17].因为有用信息被掩盖在混沌信号中，而混沌信号在小波域中的能量谱中相对集中，但噪声的能量谱却比较分散，并且混沌信号在小波域中的分解系数绝对值比噪声中的大.因此，可以利用小波变换原理对信号进行多尺度分解，然后选择适当的阈值，过滤掉绝对值相对小的小波系数，从而进行分层分尺度去噪，达到降低噪声的效果，最后把去噪处理后的信号进行重构，则可得到原有用信号.

选取如图3所示的保密通信方法，选用离散信号h(t)进行传输，则传输的混合信号s(t)=h(t)+x22(t)+n(t)，其中n(t)是5 dB的高斯白噪声信号.

令节点1为发射系统，有：

令节点2为接收系统，有：

图6为加入高斯白噪声后含噪信号的传输与小波去噪的Matlab数值仿真结果.其中：图6(a)为x22的时间序列；图6(b)为有用信息h(t)；图6(c)为信道中第一次加密后传输的含噪信号s(t)；图6(d)为信道中第二次加密后传输的含噪信号s′(t)；图6(e)为第一次恢复的信号h′(t)；图6(f)为第二次恢复的信号h″(t)；图6(g)为采用小波阈值去噪处理后的有用信号h1(t).

图6 离散信号去噪示意图

从图6(f)可以看出，在加入高斯白噪声影响的情况下，尽管有用信息可以被大致恢复出来，但是由于它在传输中受到噪声干扰而发生了变化，波形振荡不够光滑.而图6(g)是在选取合适的阈值后，经过小波变换处理，使有用信号可以很好地恢复出来，去噪效果比较良好.

4 结论

本文提出了一个新的四维混沌系统，并验证了其吸引子的存在.研究了基于该系统的全局耦合网络的渐近同步问题.在此基础上将其同步应用到保密通信中，研究了2个节点之间进行多次加密的新保密通信系统，并且在信息传输中加入高斯白噪声的干扰.最后，在小波变换的作用下，经过调节阈值对有用信息进行去噪处理，最终有用信息能够很好地无失真地恢复出来.