求解互补问题的改进粒子群算法研究
刘 铭,董立娇,王秀玉
(长春工业大学数学与统计学院,吉林 长春 130012)
互补问题在经济、二次规划、建筑等领域深受广大学者关注.求解互补问题的方法有许多,例如光滑牛顿法、非光滑牛顿法、内点法等.但普通求解互补问题的数学方法对初始点的要求很高,并且依赖梯度信息,从而导致很难求出互补问题的解.这就需要研究人员结合其他方法进行转化,以提高求解互补问题的效率.
随着计算机技术的发展,出现了许多计算优化问题的智能算法.其中应用较广的是粒子群算法(PSO)、遗传算法、人工神经网络等.智能算法在求解互补问题中的应用比较少,应用智能算法计算互补问题可以规避传统求解互补问题过程中对初始点选取和梯度信息依赖的问题.本文通过改进标准粒子群算法中的惯性权重以及引入收缩因子,结合凝聚函数[1]提出了一种准确率高、收敛速度快的求解互补问题的智能优化算法.
1 互补问题的模型研究
通常情况下,互补问题指:对任意x∈Rn,F:Rn→Rn,有
x≥0,
(1)
F(x)≥0,
(2)
xTF(x)=0.
(3)
当F(x)为线性函数,即F(x)=Mx+q(M为n×n矩阵,q为常向量)时,称为线性互补问题(LCP);当F(x)为非线性函数时,称为非线性互补问题(NCP).
称函数g(a,b):R2→R为NCP函数,如果g(a,b)=0⟺a≥0,b≥0,ab=0.
常见的NCP函数有:
(4)
(5)
求解非线性互补问题等价于求解如下优化问题的极小值[2]:
(6)
(7)
所以求解NCP可以转化为求解下列非光滑方程组问题:
[g(x1,F1(x)),g(x2,F2(x)),…,g(xn,Fn(x))]T=0,i=1,2,…,n.
(8)
这是一个较难的不可微优化问题,经典的光滑牛顿法对初始值的依赖性较高,因此用其计算起来比较困难.为克服非光滑性,产生了多种对NCP函数进行光滑化的方法.
为了求出互补问题[3]在x≥0,f(x)≥0时xTf(x)=0的解,可以采用极小算子的光滑逼近的形式[4]
(9)
其中μ>0.
同样通过光滑化[5],可将(4)式光滑化为
(10)
其中ε>0.
本文借助于凝聚函数将非线性互补问题转化为无约束优化方程组,应用凝聚函数[6]
(11)
对max函数进行光滑化,使得对任意μ,gμ(x,f(x))=-μ*ln{exp(-x/μ)+exp(-f(x)/μ)}.由关系式[7-8]
-max{-x,-f(x)}-μln2≤-μln{exp(-x/μ)+exp(-f(x)/μ)}≤-max{-x,-f(x)},
当μ→0时,gμ{x,f(x)}一致收敛于gμ{x,f(x)},且gμ{x,f(x)}的每一分量有近似光滑函数
gμ{xi,fi(x)}=-μln{exp(-xi/μ)+exp(-fi(x)/μ)},i=1,2,…,n.
(12)
(12)式即为方程组(6)的近似.
综上,将求解互补问题转化成了求解非线性光滑方程组的解,取μ的单调递减函数并趋于0,通过凝聚函数给出了一种求解(6)式的方法.下面应用改进的粒子群算法给出更适合求解互补问题的优化算法.
2 基于互补问题的改进粒子群算法研究
2.1 标准粒子群算法
将粒子群算法应用到求解互补问题中.算法中的每一个粒子都代表互补问题中的一个解,粒子在迭代过程中计算自身适应度值,并在寻优过程中会动态调整自身的速度和位移,通过比较个体极值和群体极值,寻找最优个体位置.[9]个体极值表示群体中个体所经历的所有位置的最优值,群体极值指群体中所有粒子中的最优值.通过循环迭代,搜索到互补问题的最优解.
设搜索空间为D维,其中有n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子的位置用一个D维的向量Xi=[Xi1,Xi2,…,XiD]T表示.通过计算并比较粒子在各个位置上的适应度值,可得出个体极值;在群体优化过程中,所有粒子经过的最优极值为群体极值.第i个粒子的速度用一个D维的向量表示为Vi=[Vi1,Vi2,…,ViD]T.
在每一次迭代过程中,粒子通过个体极值和全局极值更新自己的速度和位置[10],更新公式如下:
(13)
(14)
其中:c1,c2∈[0,1]为加速因子,通常c1,c2取常数时可以得到较好的最优解;w为惯性权重,通常取常数d=1,2,…,D;i=1,2,…,n;Vid为粒子速度;Xid为粒子位置;r1,r2∈[0,1]为随机数.为防止粒子在搜索过程中出现冗余,通常将粒子速度和位置限定在一定区域[-Xmax,Xmax],[-Vmax,Vmax].具体PSO算法流程见图1.

图1 PSO算法流程图
2.2 改进的粒子群算法
2.2.1 线性递减惯性权重的粒子群算法(W-PSO)
在标准的速度更新公式中引入线性递减惯性权重[11],惯性权重w可以影响粒子的局部寻优能力和全局寻优能力,这里选择线性递减惯性权重为
(15)
其中:k为当前迭代次数;wk为当前迭代惯性权重;wmax和wmin分别为最大惯性权重和最小惯性权重;kmax为最大迭代次数.因此,根据(15)式速度迭代公式变为
(16)
综上所述,粒子群算法在求解非线性互补问题的极值方面应用广泛.在约束范围内,通过调节粒子群算法中的参数[12-13]来计算种群中每个粒子的适应度值,并通过不断的迭代比较个体适应度值和全局适应度值,最终得到相应的最优解.应用粒子群算法可以求解很多复杂的互补问题,避免求不出可行解的情况发生.通过改进的粒子群算法,提高了求解非线性互补问题的准确性.
2.2.2 引入收缩因子的粒子群算法(W-CPSO)
为提高算法的收敛速度,在对标准PSO算法速度更新公式引入线性递减权重的前提下,在(16)式基础上引入收缩因子[14-15]:
(17)
(18)
φ=c1+c2,φ>4,xi=xi+vi.
(19)
在标准的粒子群算法下,通过改进惯性权重和引入收缩因子,使算法不再陷于局部寻优,提高算法寻优的准确率和收敛速度.
3 实例分析
为了检验本文所改进的粒子群算法在求解互补问题中的性能,选择了在许多互补问题论文中所列举的例子.通过应用标准粒子群算法、改进惯性权重的粒子群算法以及在改进惯性权重的基础上在速度更新处引入收缩因子来提高粒子群计算效率.
为解决以下互补问题,选取种群规模为1 000,最大进化代数为500,权重由wmax=0.9线性递减到wmin=0.4,设置容许误差为e<0.01.
例1求解非线性互补问题中的Kojima-Shindo问题[8]:
首先应用传统PSO算法进行计算.设置参数p=1 000 000,c1=c2=1.494 45,w=1.随机产生初始点对上述实例进行20次重复计算,选择出在容许误差e<0.01范围内符合条件的最优解,结果有12次搜索到最优解;其次,在标准PSO算法的基础上调整w的值,使w呈线性递减变换,同样进行20次重复计算,得到的结果显示搜索的准确率明显提高:20次计算在容许误差范围内都能搜到使互补问题接近于0的最优解,并且搜索速度比标准PSO算法的速度更快.为进一步提高计算的收敛速度,在改进惯性权重的PSO算法中引入收缩因子,结果显示收敛精度远远超过标准PSO算法.三种算法的验证结果分析见表1,收敛速度见图2.

表1 三种算法20次验证结果分析
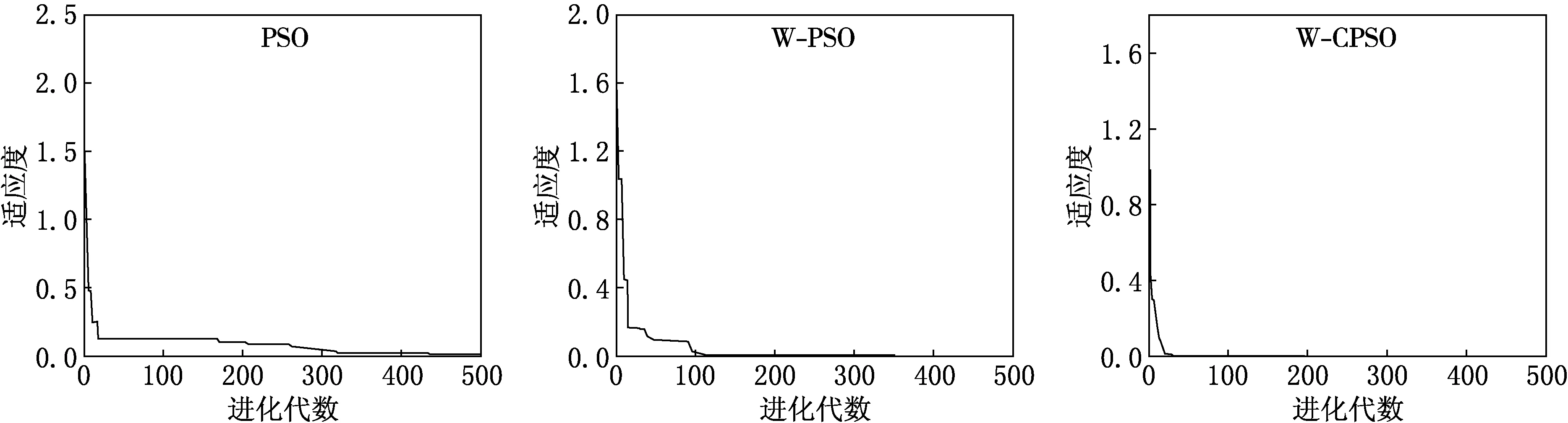
图图2三种算法收敛结果
例2求解线性互补问题F(x)=Mx+q,其中矩阵M和向量q由下式给出:

此线性互补问题的解为xT=(0.5,0,0.5,0,0.5),应用上例所用的方法得到的结果如表2所示.

表2 三种算法20次验证结果分析
由例1—2,可见在传统PSO算法的基础上,线性改进惯性权重不仅增加了算法的准确性,而且在速度更新处添加收缩因子后,在保证准确率的基础上提高了算法的收敛速度.这避免粒子在寻优过程中过早收敛,保证了粒子的活跃性,同时也避免了在搜索过程中粒子都是向全局最优靠近的同一性.在解决互补问题时不用考虑初始点和导数信息的情况下,更好更快的得出问题的结果.
4 结束语
通过改进标准粒子群算法中的惯性权重并且引入收缩因子,并结合凝聚函数来求解互补问题,不但提高了算法的准确率和收敛速度,而且本文粒子群算法在计算互补问题时不依靠初始点的选取和梯度信息,不仅给求解互补问题提出了新的方法,同样也扩展了智能算法在互补问题求解方面的应用范围.实验结果表明,改进的粒子群算法准确率高、稳定性好、收敛速度快,是求解互补问题的一种有效算法.

