于不严谨处严谨,发展学生科学精神
安徽六安市人民路小学东校(237010)
教师在教学中会遇到命题不严谨的练习题,经常采取的做法是不选择这样的习题进行练习。但就是因为这些命题上有漏洞的练习题,反而比其他的练习题具有更大的思考空间。同时面对练习题的不严谨,教师的“忽略”处理也是一种不严谨的态度和做法。如果在不严谨的练习题中严谨对待,必然能培养学生的质疑态度,促进学生去经历推理和探究的过程,发展他们的科学精神。
一、培育理性思维,夯实基础知识
一些不严谨的练习题如涉及学科基础知识,命题者或没能准确解读基础知识,或没能准确把握学生的学习特点,导致命题与考察意图不符。教师在遇到这样的练习题时,或发现明显不合理之处,予以“忽略”;或纠结于该从学生现状出发还是从习题自身出发,最终也在纠结中“忽略”了。学科基础知识是学生已经掌握的或正在掌握的知识,若把这样的练习题在学生面前展开,让学生依据自己所学的基础知识去分析、讨论、辨别,不仅可以巩固他们的基础知识,还能够培养他们的理性思维。
【案例1】近似数练习题
一个数的近似数是10万,这个数最大是( ),最小是( )。
给定一个近似数,确定精确值的范围,此题逆向考查学生对近似数的理解和掌握情况。命题者原本考查学生对“四舍五入”的理解,即取近似数需要观察所要精确到数位的下一位,所以将答案定为104999和95000。而此题完全可以理解为精确到十万位,这样与题中的“最大”“最小”更为贴合。但是学生此时刚学习近似数,很难理解到这一层面。针对此题,笔者开展了以下教学:
首先,对学生依次提出以下3个问题:(1)你认为这个数取近似数时,精确到哪个数位?(2)如果这个数精确到万位是10万,它可能是多少?(3)如果这个数精确到万位是10万,它最大是多少?最小是多少?问题(1)提出后,学生一致认为该数精确到万位,这符合学生目前的学习水平。然后借助问题(2)和(3)巩固根据近似数确定精确值范围的知识。
接下来抛出问题:“你认为这个数取近似数时,有可能精确到十万位吗?”学生思考后明确“有可能”,并且很快确定出取值范围为50000至149999。紧接着把选择权交给学生:“这题没有明确规定精确到哪个数位,而经过尝试可知,精确到万位和十万位都可以,我们应该怎样选择呢?”学生开始进行辨析和讨论,绝大多数学生认为应精确到十万位,因为题中没有规定精确到哪个数位,但要求填最大和最小的数,那就应该按这个要求填写。但有一名学生的观点不同,她说:“我们从课本中知道,近似数是与精确值接近的数,50000和149999与10万相差太远了,而95000和104999更接近10万,所以应该精确到万位。”教材上对用“四舍五入”法取近似数的解读,确实有“更接近”这层意思(如图1),因此,有部分学生开始质疑。

图1
笔者适时出示教材练习(如图2),以25763为例把它分别用“四舍五入”法取近似数精确到十位、百位、千位、万位,再把这些数在数轴上表示出来(如图3),通过数形结合,将不同精确数位的数值特征显示出来,学生很快得出:用“四舍五入”法取近似数时,精确的数位越低,与精确值越接近。因此,在上一道题中精确到万位比精确到十万位更接近精确值的道理就不言而喻了。
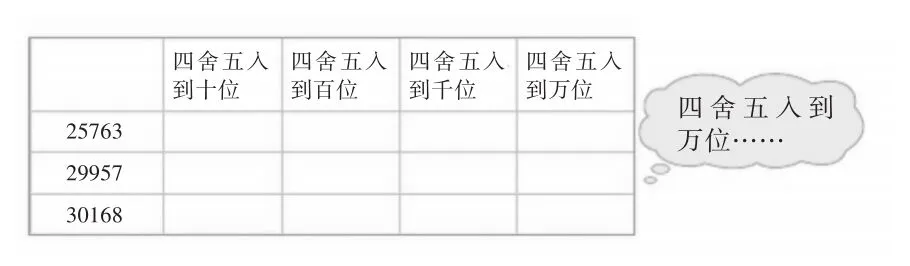
图2

图3
二、发展探究精神,拓展思维能力
一些不严谨的练习题,因其存在不严谨的地方,往往会给学生提供更广阔的思考空间。充分发掘其价值,引导学生深入探究,便能借此拓展学生的思维能力。更为重要的是能让学生充分地经历数学思考、数学探究的过程,从而使学生的探究精神得到进一步培养,探究能力得到进一步提升。
【案例2】有余数的除法练习题
用19根小棒摆正方形,可以摆出( )个正方形,剩余( )根小棒。
此题是二年级有余数的除法练习题,命题者原意可能是摆出不相连的正方形,即摆一个正方形需要4根小棒,19÷4=4(个)……3(根),可以摆出4个正方形,剩余3根小棒。由于题中没有说明摆出不相连的正方形,而学生又有摆相连图形的经验,对此,笔者尝试利用此不严谨点开展教学,引领学生深入探究,发展学生空间观念。
面对此题练习,很快便有学生发现:可以摆出6个正方形,没有剩余小棒。笔者追问:“你是怎么想的?试着把你的想法与同学分享。”该学生向大家介绍他是画图发现的(如图4)。其他学生恍然大悟,同时疑惑:这种做法没有剩余小棒,好像不符合题目要求。笔者继续引导:“看来画图确实是个好方法,你们再画一画,看看会不会有其他发现?”一番探索之后,一名学生展示了另一幅图(如图5),同样可以摆出6个正方形,而且剩余2根小棒。
图4

图5
笔者再引导学生比较,图5比图4更加节约小棒,这是为什么呢?在对比、思考和讨论后得出:图4只向右边连接,是1个方向;图5不仅向右连接,同时向下连接,是2个方向。笔者问:“继续探索,还会不会有更节约小棒的摆法呢?”学生画图探究,有的甚至画出向4个方向延伸连接的图。笔者最终出示正方体,问:“如果用小棒搭成正方体,需要几根?一个正方体上有几个正方形?”
在笔者的引领下,学生经过自主探究,经历摆不相连的正方形——向1个方向摆相连的正方形——向2个方向摆相连的正方形——摆立体图形的探究过程,他们的空间观念和想象能力得到发展。
三、培养质疑态度,提升综合应用能力
不同学科、不同学段的学科素养,都体现出其对于发展学生核心素养的“独特价值”。这种“独特价值”既是学科差异的表现,也是学科价值的体现。数学学科在培育学生科学精神方面便有其“独特的价值”。面对不严谨练习题,教师严谨地引导学生思考、辨析和讨论,理性思维和探究精神逐步得到培养,让学生不盲从书本,不盲从老师,做到独立思考、判断和解决问题。
【案例3】三角形的分类考试题
(单项选择题)一个三角形中有一个内角是91度,这个三角形是( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
考试结束后有学生主动提出质疑:这题应该有两个选项,C和D都符合要求。因为三角形中有一个内角是91度,这个三角形肯定是钝角三角形。其他两个内角和是89度,如果平均分成两份,每个角是45.5度,那么这个三角形同时也是等腰三角形,所以选C和D都可以。
听了这位学生如此全面的思考和分析,另外一名学生也提出疑问说:“我认为还是应该选择C,因为三角形的一个内角是91度,那么它肯定是钝角三角形,当然,刚才那位同学说的也有道理,有可能是等腰三角形。四年级上学期我们学习过可能性,用可能性的知识来判断,钝角三角形是确定的,而等腰三角形是不确定的,所以单项选择只能选C。”
最后一位学生综合应用了三角形分类和概率的知识进行分析,全面而深刻。批判质疑精神的特点,就是进行深入探究和理性思考后,方能提出质疑,以科学的眼光看待周围的事和物。而这也正是数学学科在培育学生发展核心素养的“独特的价值”。
总之,为了便于他人的理解,便于交流和研究的深入,数学的严谨性变得异常重要。因此,在数学教学的过程中,应当注重严谨性。但严谨性仅仅是数学思维的一个特征,而不是数学思维的本质,数学思维的本质是数学的基本思想。正如史宁中教授所说,数学教育中的“过程教育”,里面所说的“过程”不是数学知识产生的过程,也不是数学家所描述的数学思维过程,而是学生经历理解数学的思维过程。面对不严谨的练习题,以严谨的态度对待,充分挖掘其内在价值,才能让学生真正经历理解数学的思维过程。

