利用轴对称求极值在中考题中的应用

山东省枣庄市实验学校(277800) 于波

北京师范大学出版社数学教科书七年级下册习题5.3第5题如下:

如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?

图1

要解决此问题,只要作点B(或A)关于街道l的对称点B′(或A′),根据轴对称性可知:PB=PB′(或PA=PA′).

因此,求AP+BP的最小值就相当于求AP+PB′(或BP+PA′)最小,很显然当A、P、B′(或B、P、A′)在一条直线上时,两点之间线段AB′(或BA′)最小,即AP+PB′(或BP+PA′)最小.因此连接AB′(或BA′),与直线l的交点P就是要求作的奶站.如下图2和图3:

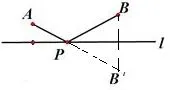
图2

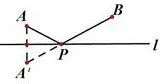
由动点产生的线段和最小值问题,是初中数学中常见的问题之一,也是中考的考点之一.这类问题一般借助轴对称将两条线段的和转化到同一条直线上,再利用“两点之间,线段最短”来解决两条线段和的最小值.现结合2018年中考试题谈一谈利用轴对称求极值在中考题中的应用.

类型之一:角中的极值问题

图4

例1(2018·山东滨州)如图4,∠AOB=60°,点P是∠AOB内的定点且,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

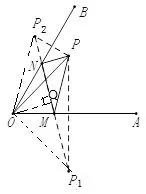
图5

解析分别以OA、OB为对称轴作点P的对称点P1,P2,连接点P1,P2,分别交射线OA、OB于点M、N则此时△PMN的周长有最小值,△PMN周长等于=PM+PN+MN=P1M+P2N+MN,根据对称的性质可知,OP1=OP2=OP=,过点O作MN的垂线段,垂足为Q,在△OP1Q中,可知,所以P1P2=2P1Q=3,故△PMN的周长最小值为3.

答案:D

类型之二:等腰三角形中的极值问题

例2(2018·四川泸州)如图6,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为___.

再生细骨料主要是建筑垃圾在破碎、筛分后得到的粒径<4.75 mm的颗粒[7]，主要由天然砂、废弃混凝土碎屑、石屑和细小粉料(如泥土)等组成。相对于天然细骨料，再生细骨料的表观密度小、吸水率高、吸水速率快，含有大量硬化水泥浆，颗粒棱角多，表面粗糙且具有较多微裂缝[8]。

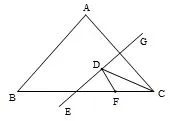
图6

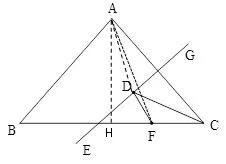
图7

解析要求△CDF周长的最小值,实际就是求出CF+CD+DF的最小值,由于CF值固定,因此要求出CD+DF的最小值.因为EG是腰AC的垂直平分线,所以DA=DC,进而转化为求AD+DF的最小值.可以作△ABC的高AH,因为△ABC的面积为120,BC=20,所以AH=12,△CDF的周长=CF+CD+DF,CF=5,因为EG是腰AC的垂直平分线,连接AD、AF,可得DA=DC,所以AD+DF的最小值为AF的长度,在Rt△AHF中,HF=5,AH=12,由勾股定理可得AF=13,因此△CDF周长的最小值为18.

答案:18

类型之三:直角三角形中的极值问题

例3(2018·湖北十堰)如图8,Rt△ABC中,AB=3,,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为___.

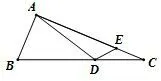
图8

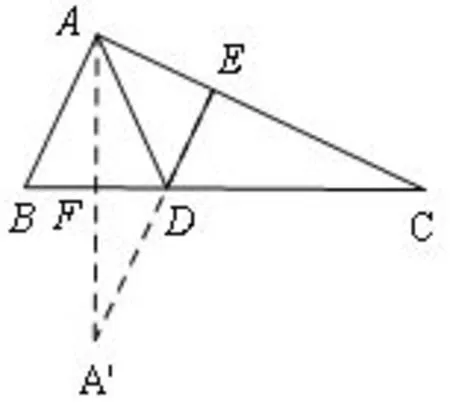
图9

解析作点A关于BC的对称点A′,连接AA′,交BC于F,过A′作AE⊥AC于E,交BC于D,则AD=A′D,此时AD+DE的值最小,就是A′E的长.Rt△ABC中,∠BAC=90°,AB=3,,所以,,所以,解得,所以,因为∠A′FD=∠DEC=90°,∠A′DF=∠CDE,所以∠A′=∠C,因为 ∠AEA′=∠BAC=90°,所以△AEA′～△BAC,所以,所以,即AD+DE的最小值是,故答案为.

类型之四:正方形中的极值问题

例4(2018·天津市)如图10,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是( )

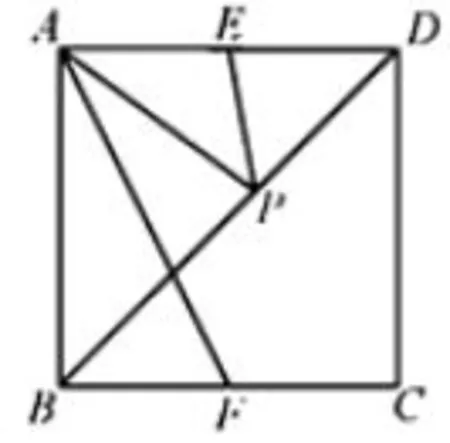
图10

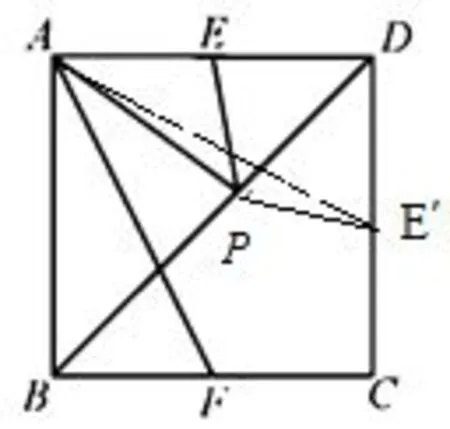
图11

解析本题考查正方形的性质及轴对称的性质,取CD中点E′连结AE′、PE′.可以取CD中点E′连结AE′、PE′,由正方形的轴对称性质,可知EP=E′P,AF=AE′,所以AP+EP=AP+E′P,所以AP+EP最小值是AE′,即AP+EP最小值是AF,故选D.

答案:D

类型之五:菱形中的极值问题

例5(2018·新疆生产建设兵团)如图12,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )

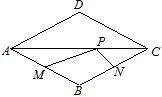
图12

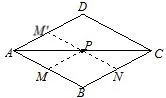
解析如图13,取AD的中点M′,连接M′N交AC于点P,则由菱形的轴对称性可知M、M′关于直线AC对称,从而PM′=PM,此时MP+PN的值最小,容易得到四边形CDM′N是平行四边形,故M′N=CD=1,于是,MP+PN的最小值是1,因此选B.

答案:B

例6(2018·广西贵港)如图14,菱形ABCD中,是BC的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

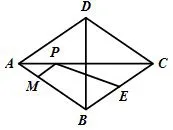
图14

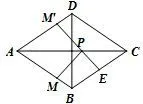
图15

解析作M关于AC的对称点,交AD与M′,显然EPM′在同一直线上,当EM′⊥AD时,EM′最短,此时PM+PN最小.依题意,,所以,即PM+PN最小值为26,故选C.

答案:C

类型之六:矩形中的极值问题

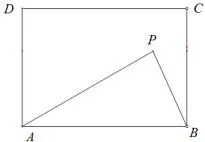
图16

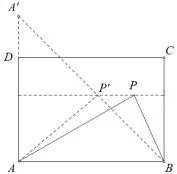
图17

例7(2018·四川攀枝花)如图16,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=,则点P到A、B两点的距离之和PA+PB的最小值为____.

解析设△PAB中AB边上的高是h,因为S△PAB=,所以,所以2,所以动点P在与AB平行且与AB的距离是2的直线l上,如图,作点A关于直线L的对称点A′,连结AA′,BA′,则BA′即为所求的最短距离.在Rt△ABA′中,AB=4,AA′=2+2=4,所以,即PA+PB的最小值为42.

类型之七:多边形中的极值问题

例8(2018·湖北荆门)如图18,在 Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.

(1)求证:;

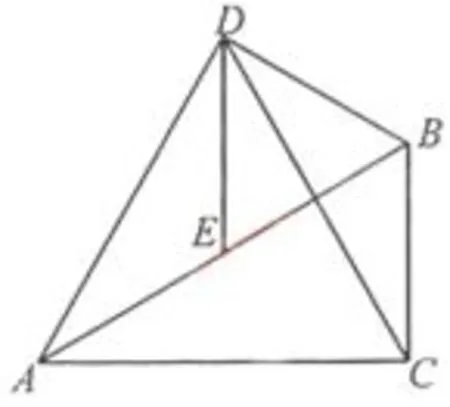
图18

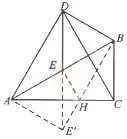
图19

解析(1)首先根据E为AB边的中点可得BC=AE,根据△DEB为等边三角形可得DB=DE,∠DEA=∠DBC,然后根据全等三角形的判定即可证明出结论;(2)作点E关于直线AC对称点E′,连接BE′交AC于点H,由作图可知:EH+BH=BE′,根据勾股定理计算即可.

证明(1)在Rt△ABC中,∠BAC=30°,E为AB边为中点,所以BC=EA,∠ABC=60°.因为△DEB为等边三角形,所以DB=DE,∠DEB=∠DBE=60°,所以∠DEA=120°,∠DBC=120°,所以∠DEA=∠DBC,所以.

(2)如图19,作点E关于直线AC对称点E′,连接BE′交AC于点H.则点H即为符合条件的点.由作图可知:EH+BH=BE′,AE′=AE,∠E′AC=∠BAC=30°,所以∠EAE′=60°,所以△EAE′为等边三角形,所以,所以∠AE′B=90°,在 Rt△ABC中,,所以,所以,所以BH+EH的最小值为3.

类型之八:抛物线中的极值问题

例9(2018·贵州遵义)如图20,抛物线y=x2+2x-3与x轴交于A、B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE、DF,则DE+DF的最小值为___.

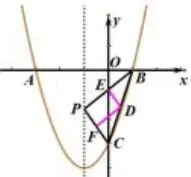
图20

解析点D、E、F分别是BC、BP、PC的中点,所以DE、DF是△PBC的中位线,,所以,从而将求DE+DF的最小值转化为求PC+PB的最小值.因为A、B、C为定点,且A、B两点关于抛物线的对称轴对称,且P为对称轴上一动点,所以PA=PB,PC+PB的最小值等于AC长度.所以连接AC,与对称轴的交点就是点P的位置,由抛物线解析式可得,A(-3,0),C(0,-3),AC=32,.

因此,在初中阶段的图形与几何中,“两点之间线段最短”是我们首先要学习的基本事实之一.在教学时要让学生掌握运用基本事实解决求两条线段之和的最小值问题的策略和方法,通过等线段代换,将所求路线长转化为两定点之间的距离.同时,还应注意利用轴对称解决最值问题应注意题目要求,根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.