浅谈基本图形分析法在几何证明题中的应用—以2018南京中考第20题为例

江苏省南京市第二十九中学初中部(210036) 孙莉

在每一年的数学中考试卷中,几何证明题是必不可少的,但在这一类的试题中,学生常出现的问题是:证明思路不清,导致推理过程颠三倒四或出现“跳跃性”的结论.究其根本原因,笔者认为这主要是学生对基本图形不熟练,在平时的几何学习中没有主动地概括反思.《数学课程标准》在几何方面的学习要求学生“能从较复杂的图形中分解出基本的图形,并能分析其中的基本元素及其关系,利用几何直观来进行思考”.

基本图形通常是指能够反映一个或几个定理,或者反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何证明题中,根据条件和结论,找出适当的一个或若干个基本图形,进而应用这些基本图形的性质,使问题得到解决,这就是基本图形分析法(1),它是解证平面几何问题的基本方法.本文以2018南京中考的第20题为例,呈现用基本图形分析法对其进行剖析及一些教学思考,与同行交流.

1、试题

(南京卷20题)如图1,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.

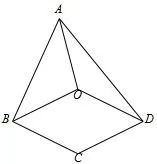
图1

求证:(1)∠BOD=∠C;

(2)四边形OBCD是菱形.

2、解法展示与分析

2.1 问题(1)

解法一利用“圆”及“圆周角定理”基本图形

因为OA=OB=OD,所以点A、B、D在以点O为圆心,OA为半径的圆上.所以∠BOD=2∠BAD.又∠C=2∠BAD,所以∠BOD=∠C.

分析由OA=OB=OD可看出“圆”的基本图形,即圆的概念“圆是到定点的距离等于定长的所有点的集合”,如图2,再结合“圆周角定理”的基本图形,如图3,可得∠BOD=2∠BAD,再利用等量代换得证.

图2

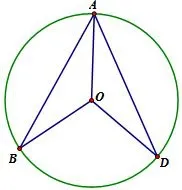
图3

解法二利用“飞镖”及“等边对等角”基本图形

如图4,作AO的延长线OE.因为OA=OB,所以∠ABO=∠BAO.又∠BOE=∠ABO+∠BAO,所以∠BOE=2∠BAO. 同理∠DOE=2∠DAO. 所以∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO),即∠BOD=2∠BAD.又∠C=2∠BAD,所以∠BOD=∠C.

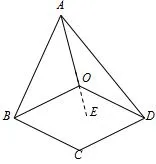
图4

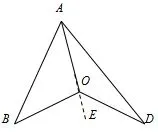
图5

分析“飞镖”模型,如图5,及其结论∠BOE=∠ABO+∠BAD+∠ADO是学生易看出的,又由OA=OB=OD结合“等边对等角”模型易得∠BOD=2∠BAD,在圆周角定理的证明过程中,“飞镖”模型是其中一种情况,即圆心在圆周角的内部,所以解法二与解法一本质是相同,只不过是把圆周角定理中的一种情形加以证明.该解法中“飞镖”模型结论的证法不止一种,这里不一一呈现,可将方法进行优化.

2.2 问题(2)

解法一利用“SSS”及“等角对等边”基本图形

如图6,连接OC.因为OB=OD,CB=CD,OC=OC,所以.所以∠BOC=∠DOC,∠BCO=∠DCO. 因为∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,所 以∠BOC=.又∠BOD=∠BCD,所以∠BOC=∠BCO.所以BO=BC.所以OB=BC=CD=DO.所以四边形OBCD是菱形.

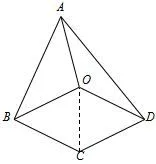
图6

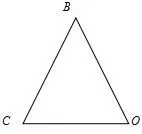
图7

分析在四边形OBCD中已有OB=OD、CB=CD,若需证明其为菱形,只需再证题中OB=CB,证明两边相等结合图形可连接OC找到“等角对等边”模型,如图7,再利用“SSS”证明即可得到∠BOC=∠BCO.

解法二利用“筝形”、“三线合一”及“等角对等边”基本图形.

如图8,连接OC、BD相交于点G.因为OB=OD,CB=CD,所以点O、C在BD的垂直平分线上.所以BG=DG,OG⊥BD.在△BOD中,OB=OD,BG=DG,所以,同理,.又∠BOD=∠BCD,所以 ∠BOC=∠BCO,所以BO=BC,所以OB=BC=CD=DO,所以四边形OBCD是菱形.

图8

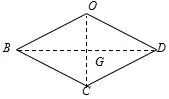
图9

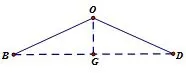
图10

分析解法一与解法二有相同之处,不同的是解法二绕过了全等,由OB=OD,CB=CD联想到筝形,如图9,利用筝形具备的性质可得OC垂直平分BD,再利用等腰三角形的“三线合一”,可得∠BOD被平分,如图11,这样的思路较解法一更清晰、书写也更简明.

解法三利用“等边对等角”及“Z”字基本图形.

如图11,连接BD.在△BOD中,OB=OD,所以.同理.又 ∠1=∠C,所以 ∠2=∠3=∠4=∠5.因为 ∠3=∠4,所以BC//OD.同理,BO//CD.所以四边形OBCD为平行四边形.因为OB=OD,所以平行四边形OBCD是菱形.

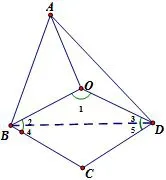
图11

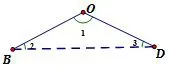
图12

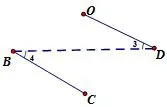
图13

分析四边形OBCD中已有两组邻边相等,若需证明其为菱形,可先证四边形OBCD为平行四边形,由OB=OD联想到“等边对等角”,如图12,从而连接BD得角相等,再结合“Z”字模型,如图13,得平行.

3、教学思考

3.1 重视基本图形的积累、加强结论证明的书写能力

数学中的基本图形一般分为两种:平面几何中的定义、基本事实及定理所对应的图形可以称之为理论型基本图形,如题中“圆”、“三线合一”、“Z”字模型;重要的例题和习题所对应的图形可以称之为经验型基本图形(2),如题中的“飞镖”模型.

前者所对应的图形往往是最基础的基本图形,为此教师必须十分重视.后者往往是由两个或两个以上简单的理论型基本图形组合而成的,是以前者的积累为基石的.它们虽不是教材上的黑体字,却是例题、习题中的“熟面孔”.从各地的中考卷中不难发现很多试题都能在教材中寻觅到他们的“痕迹”,所以我们要重视对例题、习题中的基本图形的挖掘,在教学中不断的帮助学生梳理、提炼基本图形,也可以鼓励学生自己去研究图形,发现平面几何的基本图形,在学生的知识储备中形成更大知识网,建构自己的图形体系,进而提高学生分析问题的效率及学习兴趣.

另外,在利用基本图形进行审题时,可能出现学生会识图,很快看出其中的基本图形,也能较快得到待证的结论,思维过程非常快,但是不会规范书写解题过程.如在问题(1)的解法一中,易看出点A、B、D三点共圆,但书写过程中易漏交代圆心、半径.在基本图形的教学中要有意识地训练学生对基本图形结论的“三段论”书写,可称为“几何小定式”,提高他们的书写能力,避免出现几何语言表述的不完整、混乱,真正做到言之有理、落笔有据.

3.2 遵循基本图形分析法的一般步骤

基本图形的教学应遵循“先认识,再分离,最后构造”.它们不是相互独立和割裂的,而是一个密切联系、相互交融的有机整体,基本图形的分解和构造离不开对基本图形的认识,而对基本图形的认识有利于基本图形的分解和构造.

在几何教学中,当学生面临复杂或陌生图形时,总希望找到常见图形的影子,使问题变得更直观熟悉,从而利用已有知识去解决,这就对基本图形的储备有要求并对其可以做出快速地分解.从解题教学的角度看,几何题解题思路:一是“从已知想可知”,二是由“未知想需知”.那么如何看待“可知”?就需咬文嚼字由条件图中看出有用的基本图形;又如何想“需知”?就是从条件图中找需要的基本图形.其中“看”、“找”就是分解.这里不得不提及文字命题的证明,由于不提供图形,需要由文字语言画出图形,这对学生的要求更高些,所以帮助学生养成画图的习惯是非常重要的,这是几何直观培养的重要部分,学生经历画图的过程更有利于分离出基本图形.

基本图形的构造,也就是我们常说的“补”图了.在平面几何中,如果能对基本图形的位置特征、性质、应用条件和应用方法熟练掌握,那么很多几何问题都能解决.特别是学生最困难的添置辅助线的问题,实质上就变成了补图的问题,即通过添辅助线将不完整的基本图形补全以使基本图形的性质得到应用.例如,在问题(2)的解决中,若对“筝形”这个基本图形非常熟悉,就很快联想到其对角线的特征并将其连接,从而找到解题的突破口.对于几何题,由已知条件出发,基本图形的构造产生的基本结论的应用是解法的自然之源,是解决问题的有效途径,有了基本图形,“神奇”的辅助线不再那么可望而不可及了.

3.3 慎防基本图形分析法易出现的误区

几何学习离不开基本图形,在重视基本图形分析法的教学过程中,也要防止其产生的负效应.

3.3.1 过多的依赖心理

我们学习几何,一方面要控制基本图形的数量,可对于初中阶段接触到的基本图形加以整理,但过多的基本图形不仅加重学生的负担也违背数学的思维本质;另一方面,平时要多花时间钻研例题与习题所蕴含的基本图形及其基本特征.基本图形一定是具有代表性的,加以甄选的,切忌将基本图形分析法魔性化、产生依赖,基本图形分析法实质是解题的一种手段,教师更多地培养学生分析问题、解决问题的能力.

3.3.2 只关注结论,不关注生成过程

基本图形及其结论必然是教师在教学中反复强调,学生也非常熟悉的,因此在解题过程中,尤其是在解决填空选择题时,掌握了基本图形在很大程度上可以提高解题能力及解题速度,但遇到几何证明题时学生会出现直接应用结论即把“理论型”与“经验型”混淆或者知道要去证明结论却走了很多弯路的情况,如在本题中应用“飞镖”模型的结论时,易出现直接利用该结论或是“舍近求远”不选择外角而选择三角形内角和定理、周角加以证明,这就要求学生在基本图形学习的过程中不死记硬背、不仅仅关注结论,而应重视知识结论生成的过程及方法的优化.

3.3.3 忽视基本图形之间的联系

在基本图形分析法的学习过程中应了解基本图形的演变规律,克服思维定势,重图形变式,从不同角度认识基本图形,把孤立的、零星的知识串联起来,这样才能更好地提高学生几何分析的能力.如在问题(2)的解决过程中,学生看到始终就是菱形,未曾想到菱形是特殊的“筝形”,不能从“筝形”的角度来由“已知”想“可知”,同一个图形对象往往有着不同属性,图形与图形之间也会有着某些联系,要从系统学的高度的来看待它们,加强“新旧”图形之间的联系,降低学生的的认知难度.

几何直观在研究、学习数学中是非常重要的,它也可以看作最基本的能力,教师应重视在日常教学中帮助学生不断提高这种能力.这里的几何是指图形,图形可以帮助我们把困难的数学问题变容易,把抽象数学问题变简单,所以应把让学生掌握一些重要的图形作为教学任务,即基本图形的教学.要有意识的强化对基本图形的运用,不断地运用这些基本图形去发现、描述问题,理解、记忆结果,即基本图形分析法在几何学习中的应用,这应该成为教学中关注的目标.