充分经历过程 实现经验再造—从“生活中的不等式”说起
江苏省金湖县吕良中心初级中学(211600) 乔太华
作为一种心理准备状态,任何新知的习得都必然依赖某些有关经验的参与,当已有经验与具体事件内在思路无法直接顺应时,已有经验必须经历“再造”过程,方能突破直觉定向,规避经验,实现经验的正迁移,在变化了的新问题情景中寻求到问题解决的途径.我们要依据知识的逻辑体系,解析知识的形成过程与形成方法,知识之间的互相关系,知识的数学本质,及认知所需要的必要条件和支持性等方面,对教学材料进行分析,依据数学发展规律、学生学习数学的认知规律和教育的规律来设计教学程序构建教学结构.这是一个自然、简单、动态、和谐的数学教育过程,能使学生经历完整的数学思考过程,实现数学经验的再造.下面以苏科版2014版《义务教育课程标准实验教科书·数学》七年级下册第10章第1节“生活中的不等式”为例,谈谈一些粗浅的看法.
教材分析不等式是刻画现实世界的一种数学模型,它是初中阶段学习的重点内容,而且也是后继学习函数等知识的基础.它是学习了一元一次方程、二元一次方程组之后的后续内容,贯穿于数学学习的始终,起着横贯上下的作用.
学情分析学生知道等式及方程的有关概念,熟练掌握了利用等式的性质解方程,初步学会了建立方程模型解决实际问题.
教学目标
1.感受生活中存在的大量不等关系,了解不等式的意义.
2.经历由具体问题建立不等式的过程,初步体会不等式是刻画现实世界的一种数学模型,培养学生建模能力.
3.通过类比等式探索不等式的有关概念,培养学生的观察、猜想、分析、归纳、概括的逻辑思维能力.
教学过程
一、情景导入,产生思维冲突
师:前年,小华和小红分别在跷跷板的两端,跷跷板保持平衡,那两个人的体重具有怎样的关系?(出示图片,图片略)
生:相等关系.小华的体重等于小红的体重.
师:如何用数学式子表示?
生:设小华和小红的体重分别为akg和bkg,则a=b.
师:确定实际问题中的相等关系,用字母分别表示出其中的两个量(这两个量是同类量),然后用等号联接,得到一个等式.
师:今年,小华和小红又分别在跷跷板的两端,小红一端上升,小华一端下降,那两个人的体重具有怎样的关系?又如何用数学式子表示?(出示图片,图片略)
生:不等关系.小华的体重大于小红的体重.设小华和小红的体重分别为akg和bkg,则a>b.
师:大家同意这位同学的观点吗?你能知道是怎样思考的吗?
生:和前面类似,确定实际问题中的不等关系,用字母分别表示出来其中的两个量(这两个量是同类量),然后用不等号连接,我把它叫不等式.
师:(追问)你是怎么想到用不等号连接的呢?以前有过这样的经验吗?
生:有,比较数的大小.
师:很好!我们暂且把它叫做“不等式”.
设计意图通过生活中的相等关系开始,让学生自主进行类比,自觉地用不等式来表示不等关系,目的是调动学生已有的经验,为经验再造打下基础.同时教师追问这样表示的思考依据,目的是让部分学生将自觉的经验改造的过程(缄默知识)显现出来(将经验直观化),供其他同学借鉴,可促进其他同学的经验改造.
二、情景体验,引导自建概念
师:像这种含有不等关系的例子,生活中是否大量存在呢?下面让我们一起感受一下.
学生自主完成下面的问题,并把答案写到黑板上.
1.观察生活中的图片,看存在哪些不等关系?

2.用数学式子表示生活中数量之间的不等关系:
(1)你知道右上角交通图标所表示的含义吗?如果一辆汽车行驶速度为akm/h,那么a与100之间的关系式表示为:___.
(2)在某种袋装牛奶中,每100g牛奶含xg蛋白质,yg脂肪,该种牛奶的营养成份含量如下表:营养成份表:(每100g)
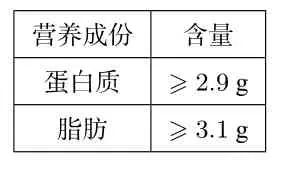
营养成份 含量__蛋白质 ≥2.9 g___________脂肪 ≥3.1 g
(3)一辆48座的旅游车载有游客x人,途中上来2个人后,车内仍有空位;
(4)小明今天锻炼身体用了t分钟,他每天锻炼身体的时间不少于30分钟;
3.用数学式子表示下面数量之间的不等关系
(1)边长为a米的正方形桌面的面积大于1m2;
(3)x-3的差不等于1.
师:刚才我们从身高、体重、公路限速、数学中的面积等方面感受到了生活中处处都有量与量之间的不等关系,并用含不等号的数学式子表示来出来.这些数学式子有别于我们学过的等式,是一种新的现象,对于一种新现象,我们要去观察它们,找到它们之间共同的本质属性,再对它们下个定义.请同学们观察上述式子,它们有什么共同点?
生:它们都含有不等号,我们把它们叫做不等式.
师:你能说说把它叫做不等式的道理吗?
生:用等号连接的叫等式,类似的用不等号连接就叫做不等式.
设计意图通过丰富的简单的例子让学生感受生活处处都有量与量之间的不等关系,尽量使不等式的类型多一点,有利于学生抓住概念的本质,更有利于学生对概念的自主建构.不等式的定义是描述性的,采用的是“像这样的…叫做…”,这就要求我们在教学时,只要抓住概念的实质即可,淡化概念的教学.通过丰富的例子,以及让学生说说为什么这样想,是为了促进经验的再造和正迁移.
三、指导应用,获得列不等式的新经验
1.根据下列具有“最”字的实例,写出不等式:
(1)火车提速后,时速v最高可达140km/h;
(2)某班学生身高h最高的约为1.74m;
(3)某班学生家到校的路程(s)最近是1km.
2.用不等式表示:
(1)a是正数;(2)b是非负数;
(3)x的一半不足-1;(4)y与4的和超过0.5;
(5)x的3倍不大于2.
师:请大家对刚才列不等式的过程进行思考?与列等式对比,总结一下列不等式的方法?
生:与列等式类似,即确定不等关系,用不等号表示,用代数式表示出不等号两边的量,列出不等式.
师:很好!我们可以把过程简单地表示为:确定不等关系,选择好不等号,用代数式表示出不等号两边的量,列出不等式.
师:列不等式的关键是什么?
生:确定不等关系,选择好不等号.
师:怎么做呢?
生:根据特殊的语言,如最大、不足、超过等,确定不等关系,选择不等号.
生:注意关键词,如正数>0;负数<0;非正数≤0;非负数≥0等.
设计意图如何列式问题,这就触及经验再造层面的方法论问题.先让学生自主列式,让“学生先来”,通过引导与等式进行对比反思,总结列不等式的一些方法与关键,这样才符合经验再造的思维次序,这里的对比是经验再造的重要途径.
五、尝试深化,强化列式经验
师:我们已经掌握了列不等式解决问题的方法,下面我们再来检验一下.
1.列不等式表示:
(1)一个数m的绝对值不小于0;
(2)两数m、n积的2倍不大于这两数的平方和.
2.表示下列实际问题中的不等关系
(1)气象台预报淮安市2018年5月13日气温是19~32°C,这表示我市5月13日的最低气温是___°C,最高气温是___°C.设我市5月13日某一时刻气温为t°C,则关于t的不等量关系是___.
(2)小丽种了一棵高70cm的小树,假设小树平均每周长高3cm,x周后这棵小树的高度不超过100cm.
(3)若一包有机肥料,包袋上印着:“净重:50kg±500g”.你能说出这包肥料的实际重量mkg是多少吗?
(4)学校准备用2000元购买名著和辞典作为科艺节奖品,其中名著每套65元,辞典每本40元,现已购买名著20套,则还能买x本辞典.
设计意图让学生再一次经历列式思考的过程,并在过程中中再一次经历经验的加深和再造,同时用没有明确关键词的第3、4小题(要挖掘隐含的实际意义建立不等式),来强化列不等式的意识,让经验变得理性和知性.
教学设计说明如果说,教学价值是教学活动的灵魂,那么数学教学的最高境界是让学生在学习数学的过程中的思维过程、方法策略内化为学生走向社会解决具体问题的基本素质、基本态度及基本思想,这一过程就是将各种学习要素转化为“生产力”的过程.当然,这是一个漫长的质变过程,需要多种环境催生,需要学生自身的裂变,更需要数学教师在教学中去挖掘和开发,在教学活动中去激发和点燃,在教学实践中去探索和发现,促进各种经验积累与再造.
本节课是从学生已有的等式的经验开始,通过设计新的情景,出现新的现象,引导学生自主进行对比和类比,不断地引导学生叙述思考的过程,将内在的缄默知识不断的外化,实现数学经验的直观化,从而利于再改造.要实施数学经验的再造,首先激活学生已有的数学经验.教师要思考的思维节点,顺应学生的思维,制造疑问,激发学生的思维冲突.
本课首先从相等到不等,从等号联想到不等号,是感性经验的直观化,挖掘联想的理由,即从数的大小迁移到式的大小,是理性经验的直观化,最后从等式到不等式,是知性经验的直观化,从概括等式的经验迁移到不等式获得概括概念的经验,从列等式到列不等式获得列不等式的经验.

