用“坐标法”解答中考“压轴题”

新疆维吾尔自治区乌鲁木齐市教育研究中心(830000) 赵爱华

数形结合思想在初中数学教学中广泛存在,对其重视,既有利于初中数学的学习,也对学生后续的高中数学学习起着重要的“启蒙”作用.“坐标法”,在初中阶段,通俗地将就是建立适当的平面直角坐标系,正确地写出点的坐标,将图形中的“数量关系”(如线段的长度,角的大小等)“位置关系”(如线段的中点,角平分线,直线的平行与垂直等)借助“坐标”数量化,然后通过“数量化”后的等式、方程(方程的解)来刻画图形的性质的方法.

下面,以乌鲁木齐市几年来的中考试题中的“压轴题”为例,感受“坐标法”的便捷,及“数形结合”数形思想的体现.

图1

例1(2016年第15题)如图1,矩形ABCD中,AB=4,BC=8,P是DC边上的动点,G是AP的中点,以P为中心,将PG绕点P顺时针旋转90°,G的对应点为G′,当B,D,G′在一条直线上时,DP=___.

解如图2,以B为原点,BC所在直线为x轴,AB所在直线为y轴,建立平面直角坐标系,则A(0,4),B(0,0),C(8,0),D(8,4).设CP=2t,则P(8,2t),依题意有,,,则x=BC+PN=10-t,y=G′N+PC=4+2t,所以G′(10-t,4+2t). 易知:直线BD的方程为,因为B,D,G′三点在一条直线上,所以,所以t=0.4,所以DP=DC-CP=4-2t=3.2.

本题解答的关键在于建立平面直角坐标系,写出直线BD的方程,用含t的代数式表示出点G′坐标,利用B,D,G′三点共线,求出t即可.

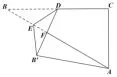
图3

例2(2018年第15题)如图3,在 Rt△ABC中,∠C=90°,BC=,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为___.

解如图,以C为原点,BC所在直线为x轴,AC所在直线为y轴,建立平面直角坐标系,根据题意可知:A(0,-2),所以直线AB的方程为.

①若∠AFB′=90°.因为在Rt△ACB中,AC=2,,所以∠CBA=30°.又因为∠BFD=90°,所以∠BDF=60°,所以∠BDE=∠B′DE=30°,所以直线DE的方程为,点E是直线DE与AB的交点,满足解得即,所以AE=3.

②若∠AB′F=90°.连结AD,因为 ∠AB′D=∠C=90°,BD′=BD=DC,AD=AD,所以Rt△AB′DRt△ACD. 所以∠B′DA=∠CDA,又因为∠B′DE=∠BDE,所以 ∠ADE=90°,即直线DE与直线AD垂直,所以直线DE的方程为:,E是直线DE与直线AB的交点,满足解得即,所以,.于是,AE的长为3或2.8.

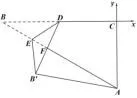
图4

图5

如果不借助“坐标法”解答本题,尤其是当∠AB′F=90°时,需要过点D作AE的垂线,然后多次利用相似,方可得到最后答案.

本题解答的关键在于建立平面直角坐标系,写出直线DE的方程,由于点E直线AB与直线DE的交点,联立直线AB与直线DE的方程,解方程组t即可.

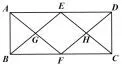
图6

例 3(2014年第 19题)如图6,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形.

解法一因为四边形ABCD是矩形,所以AD//BC,且AD=BC.又E,F分别是AD,BC的中点,所以,所以AE//CF,且AE=CF,所以四边形AFCE是平行四边形,所以AF//CE.同理BE//DF,所以四边形EGFH是平行四边形.连接EF,易知AE//BF,且AE=BF,所以四边形ABFE是平行四边形.而∠BAE=90°,所以ABFE是矩形,所以BE=AF,所以GE=GF,所以四边形EGFH是菱形.

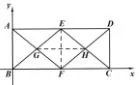
图7

解法二如图7所示,建立直角坐标系,不妨设AB=2a,BC= 2c,所以A(0,2a),B(0,0),C(2c,0),D(2c,2a),又E,F分别为AD,BC的中点,所以E(c,2a),F(c,0),所以EF//AB,所以四边形ABFE,四边形EFCD都是平行四边形,所以G,H分别是EB,EC的中点,所以,所以GH//BC,所以GH⊥EF,而GH的中点为(c,a),EF的中点也为(c,a),即GH与EF互相平分,所以四边形EGFH为菱形.

解法一,要证明四边形EGFH为菱形,需要先证明四边形EGFH为平行四边形,再证明一组邻边相等,要求学生思维要顺畅、严密.解法二,通过建立平面直角坐标系,由xE=xF,yG=yH,这一数量特征,获得GH⊥EF,又由线段GH,EF的中点均为(c,a)这一数量特征,获得GH与EF互相平分,从而使问题得到解决.

“坐标法”既是“图形与几何”内容中“图形的性质”“图形的变化”与“图形与坐标”的有机结合,也是“数形结合”“转化与化归”数学思想的体现.用“坐标法”解决问题的步骤是:①建立适当的平面直角坐标系;②写出关键点的坐标;③将图形中的位置关系数量化(方程、方程组);④用得到的数量特征解释位置关系.

《义务教育数学课程标准(2011年版)》在各学段中安排了“数与代数”“图形与几何”“统计与概率”“综合与实践”四个部分的课程内容.其中“图形与几何”(第三学段,即7-9年级)具体包括“图形的性质”“图形的变化”“图形与坐标”三部分内容.说明“图形的性质、变化”与“坐标”之间是有密切联系的.

另外,无论是从数学认知结构的角度还是从数学概括的角度探讨数学能力的实质,数学思想和数学方法都是极为重要的.实际上,由于数学认知结构是主体对数学知识结构的主观反映,而正是由于数学思想和方法的存在,才使得数学知识不再是孤立的单点或离散的片断,使得解决数学问题的方法不再是刻板的套路和个别的一招一式,数学思想和方法在数学认知结构中起着固定的作用.所以,在学习“基础知识”,训练“基本技能”,培养“能力”的同时,应该时刻关注数学思想和方法.