灰色语言犹豫模糊的灰关联决策方法及其应用——以制造业转型升级为例

张 燕，李庆胜，胡阿芹，2

（1.临沂大学 商学院，山东 临沂 276005；2.南京航空航天大学 经济与管理学院，江苏 南京 210016）

1 引言

自从Zadeh提出模糊集以来，许多学者分别研究了模糊集的拓展形式，如直觉模糊集［1］、2型模糊［2-3］、n型模糊集［2］、模糊多集［4-5］和犹豫模糊集。犹豫模糊集是在直觉模糊集，提出的一种新的概念拓展出的新表达方式。在犹豫模糊集中不需要了解隶属度的分布函数，而仅仅用几种可能的值来表示决策者的判断，这对犹豫不决的决策来说，无疑提供了一种很好的表达方法。陈鹏对犹豫模糊集及其运用研究进行了梳理，提出了已有研究存在的问题，以及可以继续的研究方向［6］。Xia研究了T和S模的犹豫模糊决策信息集成算子，将其应用于不确定性决策［7］。王晴等［8］研究了犹豫模糊语言多属性决策灰关联分析方法及其应用。多属性决策信息往往具有模糊和灰色性质，因此灰色模糊多属性决策（GFMADM）引起了学者们的研究兴趣。李庆胜［9］将犹豫模糊集拓展到灰色领域，提出了灰色犹豫模糊集及其决策方法。

利用灰色语言的性质对灰色语言犹豫模糊数据进行集结，通过灰色关联方法确定属性指标权重，利用记分函数值和灰色关联权重线性加权的方式进行方案选优，并与方法做了对比研究，通过制造业转型升级可行性的决策案例证明了方法的可行性和有效性。

2 预备知识

2.1 灰色语言集合

在一些实际的决策过程中，常常将语言值与灰度的概念结合，更像是基于灰色系统的核与灰度的描述一样，可以使得决策信息更符合决策习惯。吴建文、王坚强在研究了语言多准则决策和灰色系统的基础上提出了灰色语言集合，并探讨了基于灰色语言的多属性决策问题［10-11］。

定义1［11］设论域X，语言短语集H＝｛H0，H1，H2，…HT-1，HT｝对于∀x∈X，均存在一个语言值Hi（Hi∈H）与之对应。若x隶属于Hi的程度μHi（x）是［0，1］上的灰数，其点灰度为v（x），v（x）∈［0，1］则称:

为X上的灰色语言集合（GLS）。μHi（x）是隶属度，可以理解为x贴近于Hi的程度。v（x）与直觉模糊集不同，它不代表非隶属度而是表示决策者信息不完全的程度，也即是灰度；尽管灰度v（x）和隶属度μHi（x）之间没有必然联系，但是一般来说｜μi+vi-1｜的值越小其信度越好。

基于犹豫模糊集的信息集成与测度方面的群决策主要有：Xu和Xia等研究犹豫模糊的集结算子，并应用于决策问题［12］。随着犹豫模糊决策理论的进一步研究，本文将决策值扩展到灰色语言，提出了灰色语言犹豫模糊集合，运用灰色关联方法进行决策。

2.2 灰色语言犹豫模糊决策模型构建

假设基于灰色语言的犹豫模糊决策问题，专家组给出个备选方案A1，A2，…，Am，并给出了P1，P2，…，Pn，n个评价标准及其对应的指标权重w＝（w1，w2，…，wn）T；其中Wi表示准则Pi的权重。有序语言评价集H＝（H0，H1，…，Ht）。得出决策矩阵GHL:

决策的首要问题是要去除不同量纲的影响，对指标进行规范化。其次是研究成本型或者效益型的指标进行一致性转化。这个过程就是将决策矩阵Pm×n＝（Pij）m×n规范化为Rm×n＝（rij）m×n。无论是成本型还是指标型（Hi，μ，v）的都可以通过以下公式进行一致性转化：rij＝（HT-i，µ，v）.

定义2 由于评价准则值是以灰色语言犹豫模糊集合形式给出，数据的长度很可能不相等，设rij的长度为l，记为

其中σi表示第i项的值IH。将灰色语言模糊数的运算法则扩展到灰色语言犹豫模糊集合，对数据rij进行集结得到zij。

定义3设ɑi＝｛Hi，μi，vi｝为任意一个灰色语言数，则称：

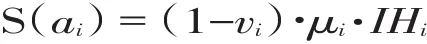
为ɑi的记分函数［11］。

ghl∈GHL，GHL＝｛（H1，μ1，v1），（H2，μ2，v2），…，（H1，μ1，v1）｝的一个灰色语言犹豫模糊元，则有：

则S（GHL）称为GHL的记分函数。

2.3 灰色关联确定权重的方法

灰色关联分析是中国学者邓聚龙在传统关联分析的基础上，提出的通过衡量单一属性值以及系统属性值的差异进行关联度相似或者相异分析的一种方法［13-15］。

定义4GHL0＝（ghl0（1）,ghl0（2），…,ghl0（n））,其中，

根据GHL0和GHL1，GHL2，…,GHLm，通过下式计算灰色联系数ζi(j)，进而得到权重w（j）：令

D＝|ghli(j)-ghl0(j)|，可得：

其中，ρ为分辨系数，ρ∈（0，1），一般取ρ＝0.5。

3 基于灰关联的灰色语言犹豫模糊决策方法

对于准则权重有些时候是已知的，在未知的情况下，可以采用灰色关联确定权重的方法来处理灰色语言犹豫模糊决策问题。利用灰色关联处理“小样本”、“贫信息”数据的优势，计算灰色关联系数ζi(j)和灰色关联度γ(j)，进而求出各个决策指标的权重值w(j)。

得到决策指标的权重值w(j)后，根据GLWAA算子可以计算各个方案的综合准则值Zi，进而可以进行Zi的大小确定方案的排序。

综上所述，可得到灰色语言犹豫模糊决策方法具体步骤如下：

步骤1将决策矩阵Pm×n＝（pij）m×n规范化为Rm×n＝（rij）m×n；

步骤2 根据式（1）对数据rij进行集结得到zij；

步骤3利用式（2）计算zij的记分函数S（aij）；

步骤4计算基于S（aij）灰色关联系数，进而得到指标权重w（j）;

步骤5 根据GLWAA算子可以计算各个方案的综合准则值Zi。

另外，在得到灰色语言犹豫模糊的S（aij）决策矩阵和灰关联权重w（j）以后，也可以直接采用公式（5）求得：

步骤6比较Zi（i＝1，2，3，4）的大小，并对方案排序。

4 算例分析

转型升级成为当前制造业发展的主流，转型升级的可行性评价成为国家和地方企业必须面对的关键性问题。市场竞争和劳动力成本上涨驱动转型升级意愿，但是以“互联网+”为特征的新业态尚未成为主流选择［16］。企业转型升级所面临的缺乏管理人才、技术支撑和资金，以及无差异激烈竞争和缺少知识产权保护也困扰着企业［17］。制造业企业家愿意坚守以及子女是否愿意成为企业家也影响着转型升级的可行性［18-21］。专家组根据下表1的动机可行性、路径可行性、宏观环境可行性以及自身可行性进行评价打分。专家组给出的评价指标隶属度值采用了灰色犹豫模糊数和灰色语言犹豫模糊数，结合灰色关联以及核与灰度等决策方法，其计算简单、直观、效果好。本文采用基于灰色关联的灰色语言犹豫模糊集决策方法对制造业的转型升级可行性进行综合评价。

表1 制造业转型升级可行性评价指标体系

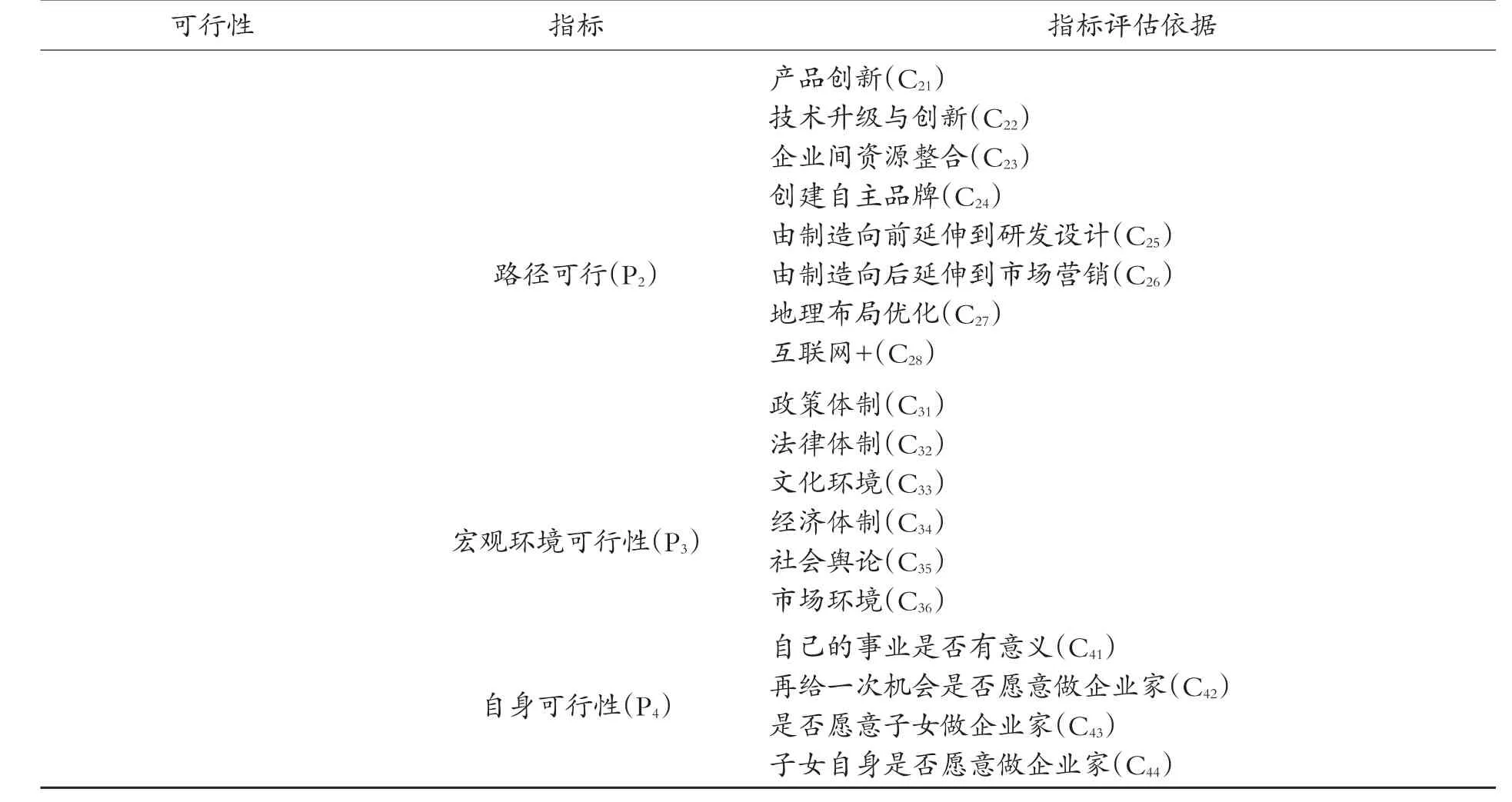
续表

主要评价指标为：动机可行性（P1）、路径可行性（P2）、宏观环境可行性（P3）以及自身可行性（P4）［16］。决策者选定：

H＝｛H0＝很差，H1＝差，H2＝较差，H3＝一般，H4＝较好，H5＝好，H6＝很好｝为语言评价术语集，评价值用灰色语言值表示，形成表2灰色语言犹豫模糊决策矩阵。

表2 灰色语言犹豫模糊决策矩阵

步骤1将决策矩阵Pm×n＝（pij）m×n规范化为Rm×n＝（rij）m×n。本算例中所有指标全部为效益型指标，故略去。

步骤2根据式（3）对数据rij进行集结得到zij，得到表3。

表3 灰色语言犹豫模糊zij决策矩阵

步骤3利用式（2）计算zij的记分函数S（ɑi）j。

步骤4计算基于S（ɑ）i灰色关联系数，进而得到指标权重。

步骤5利用GHLWAA算子计算各个方案的综合准则值Zi。

同理可得，

步骤6比较Zi（i＝1，2，3，4）的大小，并对方案排序。

可知，Z1＜Z2＜Z4＜Z3。所以，方案A3最优，方案A4次之，方案A1最差。

另外，在决策步骤4之后，在得到灰色语言犹豫模糊的S（ɑi）j决策矩阵和灰色关联权重的基础上，也可以直接利用记分函数值和灰色关联权重线性加权的方式进行选优，采用公式（5）计算各个方案的综合准则值Zi：

显然，与GHLWAA算子得到的排序完全一致，但是直接采用灰关联加权记分函数的方法更为简单。

5 结论

在多属性决策领域，多指标往往伴有模糊性和灰性，犹豫模糊决策也不例外。在对灰色语言数据集结的基础上计算灰色语言的计分函数，进而利用灰色关联确定权重进行方案排序，通过制造业转型升级可行性的案例与GHLWAA方法对比研究证明了本方法的有效性和实用性，对于类似的不确定性群决策和利用交叉方法进行决策具有一定的参考价值。