基于量本利分析法的房地产开发项目经济评价

杨芝娟 朱 朦 朱琳静 金莉婷 邬竺听 殷思齐

一、房地产开发概念及现状

（一）房地产的含义

在客观条件下，房地产就是房产和地产的总称，但在深层次上，可以认为是土地、土地上的建筑物和及其所衍生的权利[1]。

（二）房地产开发概念

房地产开发，就是房地产开发商，依据当地的城市规划，对国家建设用地开展基础设施、房屋建设的活动。

（三）房地产开发现状

目前，中国的经济在不断地发展前进，而房地产作为其中的一部分，其规模也在不断地扩大。房地产开发存在以下现象：（1）土地成片开发或出让数量大；（2）房地产市场资金流通量大；（3）政府针对房地产市场和房价的调控力度加大，房地产市场的竞争压力日益增强。

房地产企业可以通过经济分析，来加强成本控制，成本控制作为房地产企业发展的重要部分，直接关系到企业的生存和发展。通过该项目的经济评价，开发商可以实施一系列的措施以提高生产、降低成本、增加盈利、提高效益。

二、量本利分析法的基本概念及原理

（一）基本概念

“量”即为数量。在一般的情况下，量是指业务量，业务量是产量、销售量和销售额的总称。

“本”即为成本。我们把成本分解为固定成本和变动成本。固定成本是指不会因为业务量的改变而变动的成本，而变动成本是指会因为受业务量的改变而变动的成本。

“利”即为利润。利润是指收入扣除了成本价格和税金之后的余额，它是一个企业经营状况好坏的综合体现。

（二）基本原理

量本利分析也叫“盈亏分析”。它是根据业务量、成本和利润，并且进行综合分析，进而达到降低成本目的的一种有实际效益的数学分析方法。量本分析法有着广泛的应用，例如在企业经营决策、利润规划和成本目标的确定与控制等方面[2]。

（三）量本利分析法的数学模型

1、线性量本利分析法模型

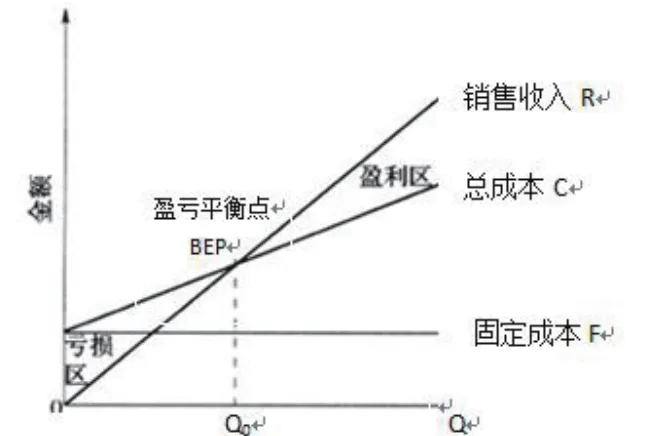
图2-1 线性量本利分析图

公式：

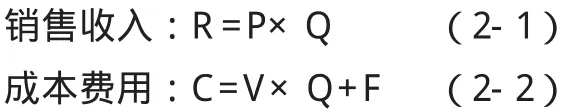
盈亏平衡年产量Q0：

BEP销售收入（R0）：

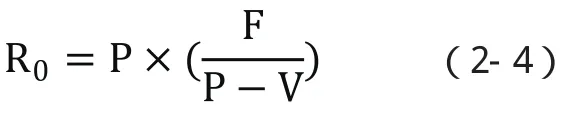
生产能力利用率：生产能力利用率

当企业的年产量大于BEP产量（Q0）时，盈利（I）：

图2-1中，总成本C与销售收入R的交点为盈亏平衡点BEP。从图中，我们可以清楚地知道，当产量时QQ0，R>C，结果为盈利，利润为R-C。盈亏平衡点的Q0减小，将会增大企业的盈利空间。

2、非线性量本利分析法模型

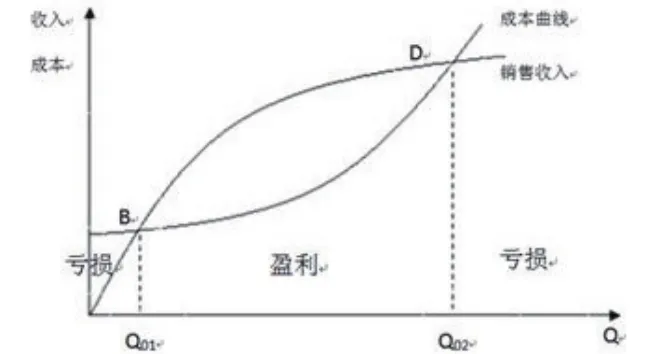
图2-2 非线性量本利分析图

图2-2中，销售收入线R与成本曲线C有两个交点，分别为B与D，横坐标分别是Q01和Q02。当产量QR，成本大于销售收入，企业亏损。当产量Q01C，销售收入大于成本，企业盈利，产量最为合理。

三、量本利分析法在房地产开发中的经济评价

（一）制定合理开发量

1、保本开发量

从图2-1中可以看出，BEP（盈亏平衡点）为房地产开发项目的销售收入线与总成本线的交点，房地产开发项目的保本开发量即为其对应的横坐标。

Q0=F/(P-V)

其中：

1.Q0——保本开发量

2.V——单位建筑面积的可变成本

3.P——单位建筑面积的销售价

4.F——总成本中的固定成本

2、利润最大时的开发量

从图2-2中可看出，当建设项目处于盈利阶段时，开发量介于经济规模Q01与Q02之间。用量本利分析法进一步研究我们即可得到在经济规模范围内实现最大盈利时的最优开发量[3]。

令销售收入曲线为函数R(Q)，总成本曲线为函数C(Q)。依据盈亏平衡原理可以知道R(Q)=C(Q)，可以解方程得两个平衡点所对应的保本产量Q01及Q02为该方程的解，也就是可求得房地产企业盈利阶段产量范围即经济规模。

销售收入减去成本为盈利，因此盈利函数I(Q)：I(Q)=R(Q)-C(Q)

利用极值原理，求得I(Q)的一阶导并当I'(Q)=0，可以得到盈利最大对应的相应产量Q。即：

I'(Q)=R'(Q)=C'(Q)

解此方程求出Q。

我们求I(Q)的二阶导来进行检验是否求得的Q为最优开发量，若如果I''(Q)<0，则最优开发量就是所求得的Q。

（二）控制企业的成本

设目标利润函数为I（Q），

I=R-C=Q(P-V)-F

式中：

1.P——单位建筑面积的销售价

2.I——目标利润

3.V——单位建筑面积的可变成本

4.F——总成本中的固定成本

5.R——总销售收入

6.Q——开发量

7.C——总成本

我们可以就能了解到获得一定利润时骑所对应的项目的合理开发量，表现为：Q=(I+F)/(P-V)

我们可以用下列公式来表示项目的单位可变成本及固定成本与项目盈亏平衡点的差值：ΔV=(P+F/Q)-V=((P-V)Q-F)/Q=I/Q

ΔF=Q(P-V)-F=I

当项目取得一定利润时，用ΔV表示项目的可变成本的变动范围，用ΔF表示项目的固定成本的变动范围。在不改变其他条件的条件下，项目的可变成本V要在盈亏平衡点V0的基础上涨幅ΔV≤I/Q，否则企业将会亏损；同时项目的固定成本F在盈亏平衡点的基础上涨幅ΔF≤I ，否则企业将会亏损[4]。

（三）企业经营状态分析

企业经营安全率可以通过量本利分析法计算得出，并以此来反映企业经营状况好坏。同时企业经营安全率也是一项重要指标。

经营安全率=(Q1-Q0)/ Q1/×100%

式中：Q0——实际或计划产销量

Q1——盈亏平衡点产销量

一般可根据下表数据进行判断：

表3-1 安全经营率判断表[5]

房地产企业的经营状况可以通过安全经营率较好反映，和安全性高低等其他情况，使科学化、合理化在项目建设之前的决策中很好体现。

四、案例分析

（一）房地产开发中的量、本分析

本文以“建筑面积”为“量”，“本”则可分作固定成本和变动成本。在房地产开发项目前期，量本利分析就显得尤为重要，从建筑面积、成本和利润之间的关系着手分析并研究，计算出项目方案在盈亏平衡时产量和单价以及成本的临界值，并且在应用时考虑企业项目的主观及客观条件变化情况，可使项目的经济评价及预测决策更加科学及符合客观实际。

（二）案例

某房地产企业有项目位于浙江省嘉兴市海宁市海昌大道与江南大道交汇处，该项目总建筑面积为15386平方米，该项目分为地上和地下部分，地上的总建筑面积共有11326平方米，而地下总建筑面积有4060平方米。该房地产公司所建住宅共有11326平方米，每平米售价为21000元/m2；该项目有共1100平方米的地下储藏室，售价为4100元/m2；共136个车库，售价100000元/个。该房地产开发项目总成本见表4-1。

表4-1 房地产开发项目总成本表

（一）保本开发量

1、求可变成本：由表4-1可知，该房地产开发项目总固定成本是13142.33万元，总变动成本为7034.9万元，总建筑面积为15386m2，因此可求得单位可变成本为：7034.9/15386 =4572.27元/平方米。

2、进行平均单价估算：由题中所给条件可求得：住宅收益为：21000*11326=237846000.00元，可得平均价格21000元/m2；地下收益为：100000*136+4100*1100=18110000.00元；可得平均价格3579.05元/m2；因此总收益为：237846000.00+18110000.00=25595.6万元。地上建筑比例=11326/15386=0.736124；地下建筑比例=4060/15386=0.263876；由以上条件可计算出，平均单价（P）为：P=21000*0.7361 24+3579.05*0.263876=16403.03 元/m2。

3、求保本产量：保本产量：

4、进一步分析，确定项目的可行性。由于项目计划开发量(Q1)为15386 m2>11108.6101m2，且Q1>Q0，所以该项目可行。

（二）企业经营状态分析

可得，该项目的：

根据表3-1,27.8%∈[25%,30%]，所以可判断出该项目经营状态为比较安全。

（三）企业成本费用控制

1、求该项目单位可变成本

项目的固定成本与项目盈亏平衡点的差值、单位可变成本与项目盈亏平衡点的差值计算公式如下：

经计算，本项目的目标利润I是4579.61万元，该项目建筑面积Q为15386平方米，而固定成本在盈亏平衡点时的为13142.33万元，单位可变成本为4572.27元/平方米。

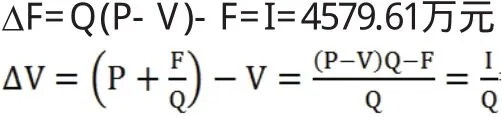
=45796100/15386=2976.48元/平方米

2、分析固定成本的控制范围

以上计算结果可表明，在不改变其他条件情况下，该项目的可变成本在盈亏平衡点（4572.270元/平方米）的基础上涨幅必须小于2976.48元/平方米，反之企业将亏损；而该项目只有让固定成本在盈亏平衡点（13142.33万元）的基础上涨幅小于4579.61万元，企业才不会亏损。

（四）最佳开发量

本案例根据本公司现有的开发技术水平并依据大量经验数据后，在前期估算出相应建筑面积下的开发成本和收益。在分别对大量的成本和收益离散点进行回归拟合后，通过EQCEL表可得到所需的两个函数（如图4-1）。由下图可看出，该图并没有从（0,0）点开始计算，但是所选取的建筑面积范围（包含两个保本点）是满足计算要求的，因为我们的目的是通过非线性量本利分析在两个保本点之间求出最大盈利值，（0,0）点并不影响结果。虽然有个别点偏离回归曲线，但并不会影响整体回归函数。

图4-1 成本、收益、利润的回归曲线图

求最佳开发量具体步骤如下：

1、求I(Q)

根据图4-1，拟合的成本及销售收入的回归函数分别为：成本函数：C(Q)=0.0009Q2-27.106Q +227031。销售收入函数R(Q)=-0.0003Q2+11.419Q-75749。则利润函数为：(Q)=R(Q)-C(Q)=-0.0003Q2+11.419Q-75749-(0.0009Q2-27.106Q+227031)=-0.0012Q2+38.525Q-302780。即利润函数：I(Q)=-0.0012Q2+38.525Q-302780。利用极值原理，令I'(Q)=-0.0024Q+38.525=0，得Qm=16052.08

2、通过对I(Q)求二阶导数并与0进行比较，判断求得的Q是否就是最大盈利时的最优开发量：

因为I''(Q)=-0.0024<0，由极值定理得，Qm是I(Q)在所选取你范围内的最大值。

3、分析

因为目前该项目的开发建筑面积为15386平方米，而总销售收入为25595.6万元，所得总利润=销售收入-总成本=5418.37万元，而本案例最佳开发建筑面积通过计算分析为16052.08平方米，此时利润最大为I(Qm)=6423.255万元，净利润可比目前增加6423.255-5418.37=1004.885万元。

五、结语

在这房地产市场竞争相当激烈的时代，前期决策的能力和对待开发项目准确的经济评价对一个开发项目的企业尤为重要。此外，房地产开发企业必须对项目的运营后期采取及时有效的措施。而本文所讨论的量本利分析法，在房地产开发项目前期的决策阶段，借助之前项目开发的数据和行情采取深度有效的经济评价，得到项目开发的保本的开发量及最佳的开发量，成功有效地提高房地产开发项目前期决策水平。