体积学习中的三种意识
2018-12-14 13:16冯克永
中学生数理化·高一版 2018年11期
■冯克永
空间几何体的体积问题是高中数学的重要内容之一,在高考中占有一定的比重。体积是考查空间想象力的有效载体,化归与转化的思想方法是破解体积问题的有效方法。下面介绍体积学习中的三种意识,以供同学们参考。
一、转化意识
当给出的几何体比较复杂,有关的计算公式无法运用,或者几何体不复杂,但条件中的已知元素彼此离散时,可采用“割”“补”的技巧(本质是等体积转化法),进而转化为易求解的几何体的体积。
例1 求棱长为a的正四面体ABCD的体积。
解:如图1,将正四面体ABCD补成一个正方体,则正方体的棱长为
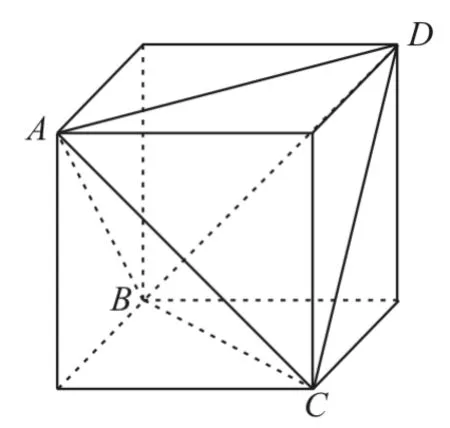
图1
故所求的体积V=V正方体-4V三棱锥=
二、交汇意识
由于体积计算融数、形于一体,具有几何与代数的“双重身份”,它因而成为中学数学知识的一个交汇点和联系其他知识的桥梁,也为高考增添了一道亮丽的风景线。
例2 在棱长为1的正方体内,有两球相外切,并且又分别与正方体相切。
(1)求两球的半径之和。
(2)当两球的半径分别是多少时,两球的体积之和最小?
解:(1)解题时,可化立体图形为平面图形求解。如图2所示,长方形ABCD为过球心的对角面,其中AB=1,AC=3。

图2
设两球的半径分别为R,r,则R+
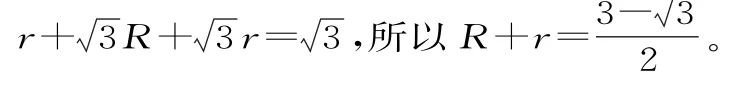
(2)设两球的体积之和为V,则


三、应用意识
学以致用,用以促学。同学们只有具有了应用意识,才能为知识的应用找到生长点,也才有可能进一步探索其应用价值。
例3 已知正方体ABCD-A"B"C"D"的棱长为1,求直线DA"与AC之间的距离。
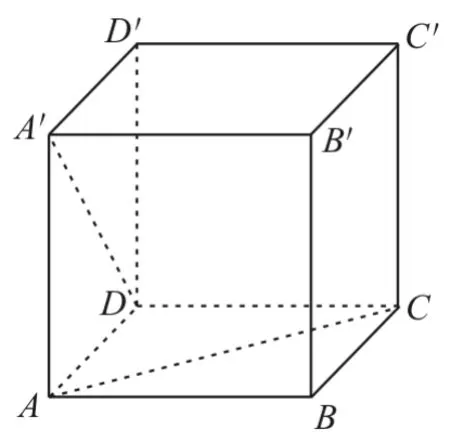
图3
解:解题时直接寻找公垂线段较难,因此可转化为求平行直线与平面之间的距离。
因为AC∥面A"C"D,所以直线DA"与AC之间的距离可转化为点A到面A"C"D之间的距离,设其距离为h。由VA-A"C"D=VC"-A"AD,可得

猜你喜欢
小学生学习指导·高年级(2023年2期)2023-09-17
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论
物理与工程(2020年1期)2020-06-07
小学生学习指导(高年级)(2019年11期)2019-11-27
小学生学习指导(高年级)(2019年3期)2019-11-27
中学教学参考·理科版(2014年3期)2014-04-10
数学大世界·小学中高年级辅导版(2009年3期)2009-04-14
中学数学研究(2008年9期)2008-12-09
中学生数理化·高二版(2008年11期)2008-06-17
中学数学杂志(高中版)(2008年1期)2008-02-23

