空间几何中的创新问题聚焦

■刘大鸣(特级教师)

近几年高考对空间几何的考查始终是围绕“空间问题平面化和模型化”展开的,下面对其创新问题进行聚焦。

创新1：由三视图判断几何体的特征

例1 某四棱锥的三视图如图1所示,在此四棱锥的侧面中,直角三角形的个数为____。

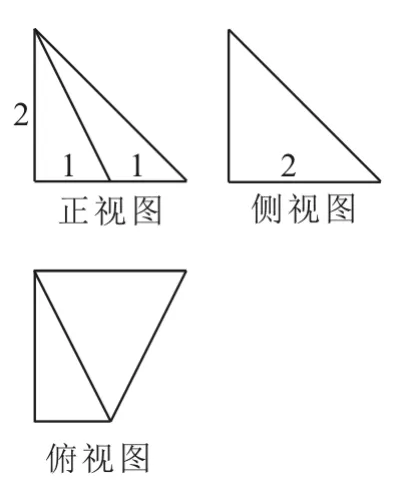
图1

解：根据三视图中有两个直角三角形的特征来还原几何体。由三视图可得正方体内的四棱锥P-ABCD,如图2所示。

图2

在四棱锥P-ABCD中,PD=2,AD=2,CD=2,AB=1,容易得到3个直角三角形,即△PAD,△PCD,△PAB。答案为3。

回味：由三视图判断几何体的特征的关键是正确还原出直观图,在还原直观图时要利用三视图的特征:正俯一样长,俯侧一样宽,正侧一样高。

变式1：某几何体的三视图如图3所示(单位:cm),则该几何体的体积(单位:cm3)是____。

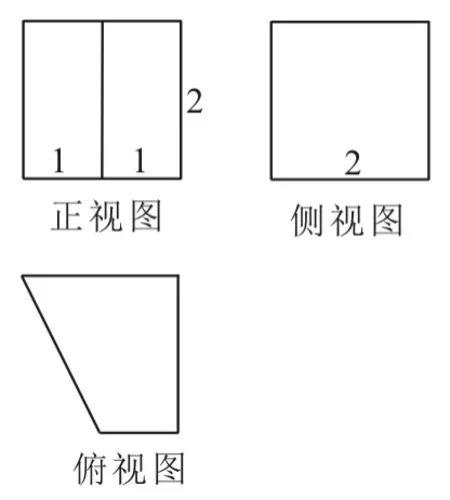
图3

提示：根据三视图可知该几何体为一个直四棱柱。直四棱柱的高为2,底面为直角梯形,梯形的上下底的边长分别为1,2,梯形的高为2,因此该几何体的体积为6。

创新2：旋转体的表面积或体积的计算

例2 如图4,已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成的角为45°,若△SAB的面积为5,则该圆锥的侧面积为 。______

图4

解：根据条件求出圆锥的母线SA,SB及底面圆的半径长,再利用圆锥的侧面积公式求解。设S在底面上的射影为O,底面半径为r,则SO⊥底面ABO。

回味：解答本题的关键是找出母线与底面所成的角及两母线的夹角,利用平面几何知识求出相应线段的长。

变式2：如图5,已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成的角为,若△SAB的面积为8,则该圆锥的体积为____。

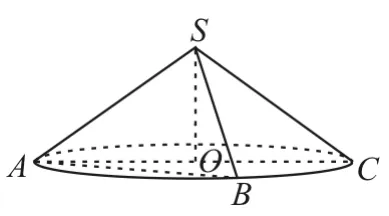
图5

创新3：几何体的表面积或体积的计算

例3 如图6所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为___。

图6

解：先分析组合体的构成,确定锥体的高,再利用锥体的体积公式求出结果。由图6可知,该多面体为两个全等正四棱锥的组合体。正四棱锥的高为正方体棱长的一半即为1,底面正方形的边长为2,所以该多面体的体积

回味：求解组合体的体积问题,关键是准确理解几何体的定义,真正把握几何体的结构特征。本题其实是求正八面体的体积,可将正八面体分割为两个全等的正四棱锥求解。

变式3：如图7,已知正方体的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M,则四棱锥M-EFGH的体积为_________。

图7

创新4：“平移法”求解异面直线所成的角

例4 如图8,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=23,∠BAD=90°。

图8

(1)求证:AD⊥BC。

(2)求异面直线BC与MD所成角的余弦值。

解：由面面垂直证明线面垂直,进而得到线线垂直,再利用中位线得到异面直线所成的角。

(1)由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC。

(2)取AC的中点为N,连接MN,ND。由M为棱AB的中点,可知MN∥BC,所以∠DMN为异面直线BC与MD所成的角。

由AD⊥平面ABC,可得AD⊥AC。在Rt△DAN 中,由AN=1,可得DN=

回味：已知两条异面直线a,b,经过空间任一点O作直线a"∥a,b"∥b,a",b"所成的角的大小与点O的位置无关,把a",b"所成的锐角(或直角)叫作异面直线a,b所成的角(或夹角)。为了简便,点O通常取在异面直线的一条上。

变式4：如图9所示,在正方体ABCDA1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为______。

图9

提示：在正方体ABCD-A1B1C1D1中,由于CD∥AB,所以异面直线AE与CD所成的角为∠EAB。设正方体的边长为2a,由E为棱CC1的中点,可得CE=a,BE=5a,所以tan

创新5：利用面面垂直的性质定理作“点到平面的距离”

例5 如图10所示,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为____。

图10

解：要求四棱锥的体积,需求四棱锥的底面积和高,因此解答本题的关键是利用面面垂直的性质定理确定平面外的点在该平面上的射影位置。连接A1C1交B1D1于点O,由平面A1B1C1D1⊥平面BDD1B1,A1C1⊥D1B1,可知A1C1⊥平面BDD1B1,则A1O就是四棱锥A-BBDD的高。由AO=×AC=111111

回味：解答本题的关键是挖掘题设中面面垂直的条件,寻找所求四棱锥的高。本题的解题过程凸显“空间问题平面化”的特点。

变式5：如图11,在三棱锥P-ABC中,AB=BC=22,PA=PB=PC=AC=4,O为AC的中点。

图11

(1)证明:PO⊥平面ABC。

(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离。

提示：(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=23。

由上可得OP2+OB2=PB2,所以OP⊥OB。由于OP⊥OB,OP⊥AC,OB∩AC=O,所以PO⊥平面ABC。

(2)作CH⊥OM,垂足为H。

由(1)可得OP⊥CH,平面POM⊥平面COM。由面面垂直的性质定理知CH⊥平面POM,所以CH即为点C到平面POM的距离。

创新6：空间中“平行与垂直”的证明方法

例6 如图12,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是弧CD上异于C,D的点。

图12

(1)证明:平面AMB⊥平面BMC。

(2)在线段AM上是否存在点P,使得MC∥平面PBD?请说明理由。

解：(1)由题设知,平面CMD⊥平面ABCD,交线为CD。

因为BC⊥CD,由面面垂直的性质定理可得BC⊥平面CMD,故BC⊥DM。

因为M为弧CD上异于C,D的点,且DC为直径,所以DM⊥CM。

又因为BC∩CM=C,所以DM⊥平面BMC。而DM⊂平面AMD,故平面AMD⊥平面BMC。

(2)当P为AM的中点时,MC∥平面PBD。证明如下:

连接AC交BD于O。因为ABCD为矩形,所以点O为AC的中点。

连接OP。因为P为AM的中点,所以MC∥OP。因为MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD。

回味：证明面面关系的核心是证明线面关系,证明线面关系的核心是证明线线关系。同学们要掌握线线平行、线面平行、线线垂直、线面垂直的证明方法。

变式6：如图13,在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1。

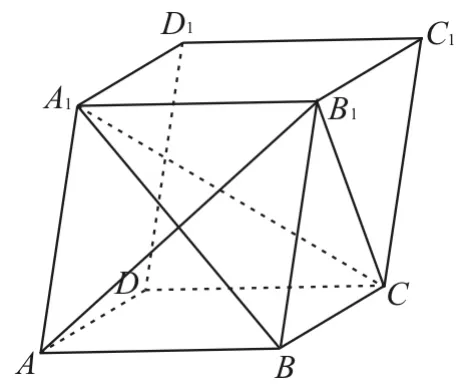
图13

求证:(1)AB∥平面A1B1C。

(2)平面ABB1A1⊥平面A1BC。

证明：(1)在平行六面体ABCDA1B1C1D1中,AB∥A1B1。

因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C。

(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形。

因为AA1=AB,所以四边形ABB1A1为菱形,可知AB1⊥A1B。

因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC。因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC。

又因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC。