空间几何体常见典型考题赏析

■朱 琴

空间几何体是立体几何的基础知识,又是每年高考的必考知识,因此学好这部分知识至关重要,特别是空间几何体的经典题型,更值得学习与探究。下面举例分析,以供大家分享。

题型1：空间几何体的三视图

对于简单几何体的组合体,在画三视图时,首先分清它是由哪些简单几何体组成的,然后再画其三视图。由三视图还原几何体时,要遵循以下三步:①看视图,明关系;②分部分,想整体;③综合起来,定整体。

例1 如图1,将一个正三棱柱ABCDEF截去一个三棱锥A-BCD,得到几何体BCDEF(如图2),则该几何体的正视图(或主视图)是( )。

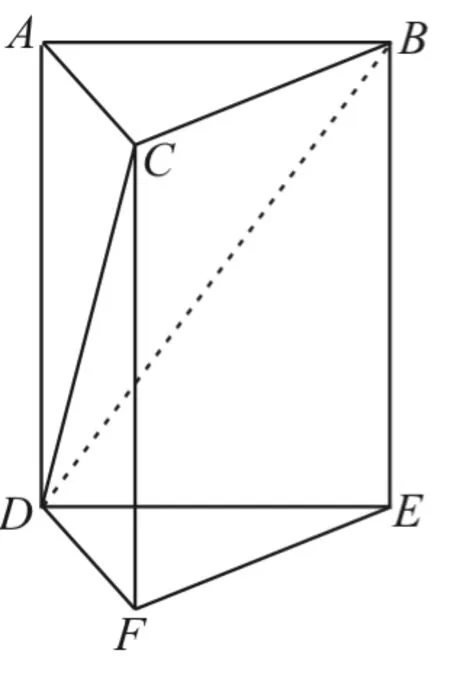
图1

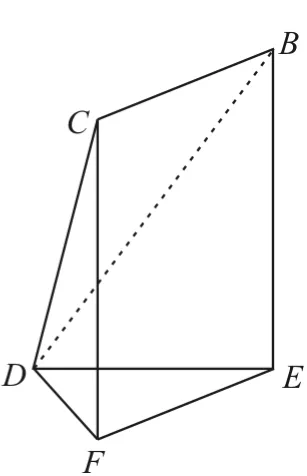
图2

解：由于三棱柱为正三棱柱,故平面ADEB⊥平面DEF。由于△DEF是等边三角形,所以CD在后侧面上的投影为AB的中点与点D的连线,CD的投影与底面不垂直。应选C。

跟踪练习1：某几何体的三视图如图3所示,记集合A为此几何体所有棱的长度构成的集合,则( )。

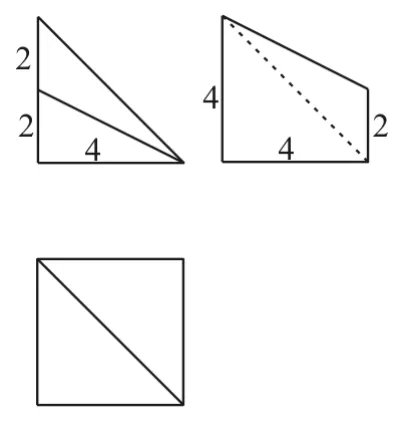
图3

A.3∈A B.5∈A

C.26∈A D.43∈A

提示：由三视图可得该几何体的直观图如图4所示。

图4

该几何体的底面是边长为4的正方形,AF⊥平面ABCD,AF∥DE,AF=2,DE=4,可求得BE的长为43,BF的长为25,EF的长为25,EC的长为42。应选D。

题型2：空间几何体的直观图

在斜二测画法中,要确定关键点及关键线段。平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半。按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积有以下关系:

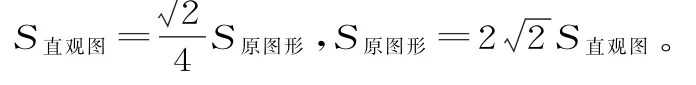
例2 已知正三角形ABC的边长为a,那么△ABC的平面直观图△A"B"C"的面积为( )。

解：图5,6所示的是△ABC的平面图形和它的直观图△A"B"C"。

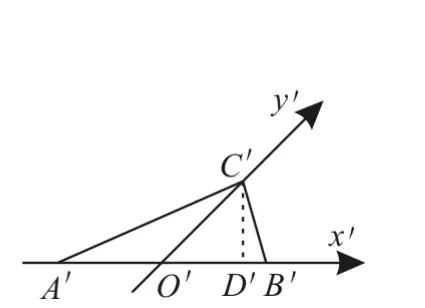
图5

跟踪练习2：如图7,已知等腰梯形ABCD中,CD=1,AD=CB=2,AB=3,以AB所在直线为x轴,线段AB的垂直平分线为y轴,则由斜二测画法画出的直观图的面积为_________。

图7

提示：作出等腰梯形ABCD的直观图,即梯形A"B"C"D",如图8所示。

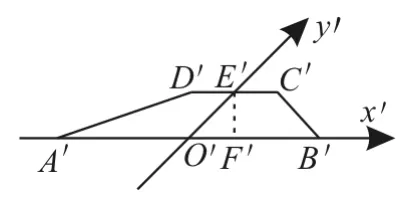
图8

题型3：与球有关的“切”“接”问题

“切”的处理方法:与球有关的内切问题主要是指球内切多面体与旋转体问题,解题时要找准切点,通过作截面来解决。“接”的处理方法:把一个多面体的几个顶点放在球面上即为球的外接问题,解题时要抓住外接的特点,即球心到多面体的顶点的距离等于球的半径。

例3 正四棱锥的顶点都在同一球面上。若该棱锥的高为4,底面边长为2,则该球的表面积为( )。

解：由题意可知,球心在正四棱锥的高上。设球的半径为R,则(4-R)2+(2)2=R2,解得R=所以所求球的表面积为4π应选A。

跟踪练习3：在封闭的直三棱柱ABCA1B1C1内有一个体积为V的球。若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )。

提示：由AB⊥BC,AB=6,BC=8,得AC=10,要使球的体积V最大,则球与直三棱柱的部分面相切。若球与三个侧面相切,可设底面△ABC的内切圆的半径为r,则×6×8=×(6+8+10)×r,可得r=2,此时2r=4＞AA1=3,不合题意。

因此球与三棱柱的上、下底面相切时,球的半径r最大。

题型4：古算书中的几何体问题

中国古代在世界上居于数学领先地位。《九章算术》记载了当时世界上最先进的分数四则运算和比例算法,还记载有解决各种面积和体积问题的算法以及利用勾股定理进行测量的各种问题。

例4 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为( )。

A.8π B.12π

C.20π D.24π

解：(方法1)将三棱锥P-ABC放入长方体中(如图9),三棱锥P-ABC的外接球就是长方体的外接球。

图9

因为PA=AB=2,AC=4,△ABC为直角三角形,所以

设外接球的半径为R。

由题意可得(2R)2=22+22+(2)2=20,即R2=5,故球O的表面积为4πR2=20π。应选C。

(方法2)利用鳖臑的特点求解,如图10。

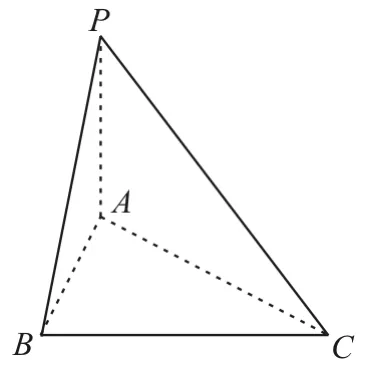
图10

因为四个面都是直角三角形,所以PC的中点到每一个顶点的距离都相等,即PC的中点为球心O,易得2R=PC=20,所以球O的表面积为4πR2=20π。应选C。

跟踪练习4：《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈。问积几何。”其意思为:今有底面为矩形的屋脊柱的楔体,下底面宽3丈,长4丈;上棱长2丈,高1丈,问它的体积是多少。已知1丈为10尺。现将该楔体的三视图给出(如图11),其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )。

图11

A.5000立方尺

B.5500立方尺

C.6000立方尺

D.6500立方尺

提示：该楔体的直观图是如图12所示的几何体ABCDEF。取AB的中点G,CD的中点H,连接FG,GH,HF,则该几何体的体积为四棱锥F-GBCH与三棱柱ADE-GHF的体积之和。

图12

可将三棱柱ADE-GHF割补成高为EF=2,底面积为S=×3×1=的一个直棱柱,故该楔体的体积V=×2+×2×3×1=5(立方丈)=5000(立方尺)。应选A。