三视图问题中的题型例析

■赵梓印

空间几何体的三视图和直观图是新课标教材中的新增内容,也是高考考查的热点,考题类型常以选择题或填空题的形式出现,常见题型有:图形判断问题,求面积问题,求三视图中的未知量问题等。

题型一：判断正视图

例1 已知三棱锥的俯视图与侧视图如图1所示,其中俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )。

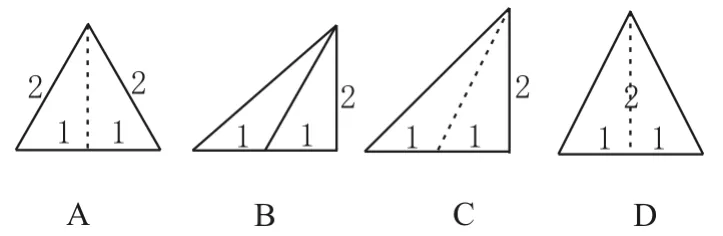
解：空间几何体的正视图和侧视图满足“高平齐”,可知正视图的高一定是2;正视图和俯视图满足“长相等”,可知正视图的底面边长为2。根据侧视图中的直角说明这个空间几何体最前面的面垂直于底面,这个面遮住了后面的一个侧棱。应选C。

空间几何体的三视图是从正面、侧面、上面三个方向对一个几何体的全方位透视。一个几何体的正视图和侧视图的高度一样,正视图和俯视图的长度一样,俯视图和侧视图的宽度一样。

题型二：根据三视图求几何体的侧面积

例2 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”。已知某“堑堵”的三视图如图2所示,则该“堑堵”的表面积为____。

图2

解：由三视图知,该几何体是底面为等腰直角三角形(斜边的边长为2)、高为2的直三棱柱,所以该几何体的表面积为2×2+

解答这类问题的关键是根据三视图所提供的图形信息,弄清楚几何体的形状和有关数据,然后求出其表面积。

题型三：求三视图中的未知量

例3 图3是一个体积为10的空间几何体的三视图,求图中x的值。

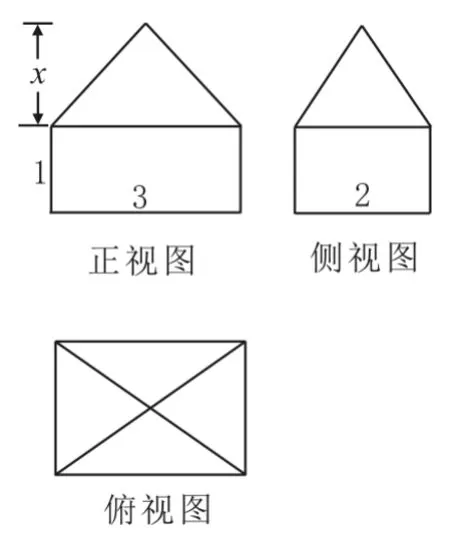
图3

解：由三视图可知,该几何体对应的直观图是一个长方体和四棱锥的组合体,所以该几何体的体积V=3×2×1+×3×2×x=10,解得x=2。

解题时要注意题中的x是四棱锥的高,而不是斜高。