数学课：让思辨意识落地生根

☉江苏省宿迁市钟吾初级中学张扬

☉江南大学附属实验中学庞彦福

数学家哈尔莫斯说过：问题是数学的心脏.“提出一个问题往往比解决一个问题更为重要”，这是爱因斯坦的名言，他同时指出“因为解决一个问题也许只是一个数学上或实验上的技巧问题，而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想象力，而且标志着科学的真正进步.”《义务教育数学课程标准（2011年版）》（以下简称《标准》）在第二部分“总目标”中指出：“运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力”，在第四部分“教学建议”中再次提出要引导和培养学生“不断提高发现问题和提出问题的能力、分析问题和解决问题的能力”.的确，有了问题才能培养学生的思辨意识和思辨能力.《礼记·中庸》指出：“博学之，审问之，慎思之，明辨之，笃行之.”清代学者王夫之在《姜斋诗话·夕堂永日绪论外编二八》中指出：“故必极学问思辨之力……然后可以治天下国家.”因此，思辨是身处现代社会面对复杂问题时体现出来的睿智与能力.数学课该如何培养学生的思辨意识与思辨能力呢？现以笔者（江苏省特级教师张扬）执教的一节初三一轮复习课“方程有解”为例与大家分享.

一、疑问，思辨意识孕育之时

问题1：解下列方程：

这是上课伊始出示的两个解方程的例子，对于第（1）小题，化为整式方程，解得x=1，经检验x=1是增根，所以原方程无解；对于第（2）小题，去分母，得到2x-2（x-1）=1，化成一元一次方程的一般形式即得出0·x=-1，这样一来，学生确实感到束手无策.对于学生而言，（1）比较容易理解，而（2）的结果并不常见.关于x的方程ax=b无解，则a、b应满足什么条件呢？当然就是a=0且b≠0.

因为方程是含有未知数的等式，所以方程首先是等式.如果跳出方程来看等式问题，这类问题也可以这样理解：由得出2x-2（x-1）=1，去括号、合并同类项后即为2=1，这显然是不成立的，也就是说这个等式中的x无论取什么数值，都不可能使等式成立.譬如x=2时，左边=2，右边=1，当然不成立；再如x=-1时，左边=-1，右边=-，也不成立；当x=0时，左边=-2，右边=-1，亦不成立.

学生学习的过程中，问题是教师告知的还是他们自己通过探索发现的才是学与教的关键.常言道：“学起于思，思起于疑，疑起于问.”课堂提问是一种促进学生学习的方法，是一种教学手段，更是一种教学艺术.宋代教育家朱熹曾说：“读书无疑者，须教有疑，有疑者，却要无疑，到这里方是长进.”这对教学是很有启发的，值得一线教师践行.

二、思考，思辨意识发芽之始

问题2：解下列方程：

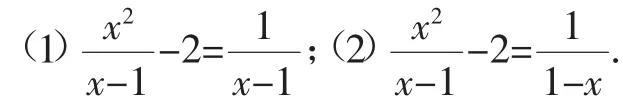
对于这组问题，去分母并整理后是一元二次方程，化简并整理后，（1）为x2-2x+1=0，（2）为x2-2x+3=0.这两个方程为什么无解呢？对于（1），学生容易存在两方面的问题，其一是忘记检验，其二是认为一元二次方程x2-2x+1=0（分解因式为（x-1）2=0）的根只有一个x=1.其实一元二次方程x2-2x+1=0的根是两个，只不过这两个根是相等的，一般写成x1=x2=1.关于方程（2），不少学生的潜意识是设法求出x2-2x+3=0的解.可是学生解着解着就感觉到有问题了，因为看似简单的一元二次方程应该可以用因式分解法求解，但不行啊，x2-2x+3不好分解呀！用配方法或公式法才发现原来是△=b2-4ac搞的鬼！因为b2-4ac=4-12=-8＜0，该方程是没有实数根的，也就是说，在实数范围内不存在能使方程成立的数，比如，当x=-3时，左边=，显然不成立；当x=0时，左边=-2，右边=1，不成立；当x=2时，左边=4-2=2，右边=-1，也不成立.

细细想想，这两个方程的无解是不一样的，第（1）题是能够求出未知数x的值，但其是增根，第（2）题是求不出来未知数x的值，所以这两者的内涵是不一样的.

变式：设计一个分式方程，使该方程化为整式方程时有两个不等的实数解，而该分式方程无解.

变式问题是开放性问题，学生是不易很快想到的，但是，一旦明白了题意，问题就显得简单了.譬如：

通过这样的尝试与思考，学生对分式方程、一元二次方程的解法中蕴含的转化思想会多一些了解，对分式方程的无解与关于x的一元二次方程ax2+bx+c=0的无解会理解得更深刻、更全面.

三、尝试，思辨意识生长之根

对于问题3，如果缺少进一步的思考与尝试，学生就无法体会到蕴含在思维过程中的分类讨论的思想与方法.问题意识、思辨意识往往就体现在学习的过程中《.标准》明确指出：“数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.数学活动经验需要在‘做’的过程和‘思考’的过程中积淀，是在数学学习活动过程中逐步积累的.”

四、体悟，思辨意识成为能力

有了对以上问题解决的经历和经验，学生很快会将问题4与问题2的（1）关联起来，于是就出现了解题中的“秒杀”现象，得出答案x=1.当教师提醒同学们多想想时，细心的学生先将原方程化为：x2-2x+2-m=0，再分类讨论.①当x=1是方程x2-2x+2-m=0的解时，得到m=1；②当△＜0，即△=（-2）2-4（2-m）＜0时，解得m＜1.即m=1或m＜1时，原方程无解.紧接着教师给出了变式1.

学生模仿问题4的解法，先由x=1得到m=±3，但是△＜0时出现m2＜9，有的学生没能正确得到m的取值范围.如果学生理解从m2＜9到m的取值范围有困难，不妨借助数轴来完成，则可顺利得出-3＜m＜3.

至此，学生则可体悟出方程无解的两种情况，一是分式方程增根所产生的，二是一元二次方程的判别式△＜0导致方程无解.

当大部分学生还在解方程组时，已有学生明白了不需要解方程组，可以借助函数图像解决.其实，关于x、y的方程组无解，就相当于抛物线y=x2-2x+3与直线y=-x+m没有公共点.进一步品味方程无解，其往往是具有几何意义的.

在本节课即将结束时，教师提出一个问题：这节课我们一起研究、讨论的都是方程（组）无解的问题，为什么课题却是“方程有解”呢？目的是引导学生进一步理解：无解只是方程的解的结果，在解答过程中体现出来的才是数学智慧和思辨能力.同时启发学生在遇到学习或生活上的困难时，要拥有“方程有解”的意识，相信总有解决的方法，这种意识对教师而言也很重要，有助于促进教师由数学教学走进数学教育.

本节课作为初三一轮复习课，贯穿初中“数与代数”板块三年所学的核心内容与知识“方程与函数”，方程知识是明线，函数知识是暗线.初三阶段的一元一次方程、二元一次方程、可化为一元一次方程的分式方程、一元二次方程都被囊括其中；函数也涵盖了所有初中阶段的一次函数（含正比例函数）、反比例函数及二次函数.可谓知识线长，知识点多，知识源丰富.学习过程包含知识与认识、方法与想法、思想与感想、体验与经验的融合.使学生在投入思维的过程中体悟数学、理解数学、享受数学.明眼人都明白我们的教育真的应该少一些“消耗式的勤奋”，我们的教学应该少一些“低水平的重复”.

可能会有人认为本节课挖的太深了，偏离了考试的要求，偏离了教学的价值.什么是数学教学的价值呢？《标准》指出：“数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养.作为促进学生全面发展教育的重要组成部分，数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创新能力方面不可替代的作用.”培养人的基本素养，培养人的思维能力和创新能力难道不是数学教学的价值吗？数学课程的核心任务就是思维的教学.思辨就是思考辨析，数学是思维的科学，思维是思辨的起点和基础.思辨意识应该是思考的时候有在自己心中和自己辩论的意识.上课不仅仅是一种教学任务，就这节课来说，更多的是一种复习课的引领，一种教学的导向，引导一线教师用研究的方法进行备课，用研究的视野进行选题，用研究的方式进行教学，追求减负增效的课堂教学，倡导提高课堂效益的教学.本节课也是一种唤醒，是唤醒学生，也是唤醒教师和教育.

学习本课，进一步提醒学生学习数学或解题时应注意多想，解题时做到“先思后做”，解决一个问题务必做到厘清楚、想明白、写规范.无论是旧课复习还是新授课，学生思维的参与是非常重要的.学生真正变成学习的主人，他们就是学习过程中的“领导者”“管理者”“创业者”，否则只能说是学习过程中的“打工者”“被动者”.学生学习数学要理解数学，其实，数学教师更应该深度理解数学，将数学知识的学术形态转化为利于学生理解和消化的教育形态，是教师理解数学的重要体现.具备数学和教学双重素养的教师，善于挖掘数学的教育价值，展示数学知识和方法的内在魅力，指导学生学会思考，学会学习.