互逆运算引出新知，数学史话融入学程——以“数的开方（第1课时）”教学为例

☉江苏省江阴市华士实验中学张威

目前初中阶段对有理数和实数都是分在不同学期进行学习，有些教材上引入数的开方、算术平方根时往往从一个生活问题出发，这些教学安排或情境引入当然有一定的道理.教无定法，若从数学知识的逻辑连续、前后一致的角度来审视“数的开方”的教学引入与起始课研发呢？笔者近期有了一次实践的机会，本文就整理该课的教学流程，并给出教学立意的解释，供分享和研讨.

一、“数的开方（第1课时）”教学流程

教学环节（一）从数及其运算说起

问题1：数，有理数，还有π，它不是有理数，是什么数呢？（如果有学生预习过能说出无理数，记得板书在黑板副板区）

问题2：有理数学习了哪些相关概念和哪几种运算？（学生能答出数轴、相反数、绝对值、倒数等，有理数的运算有加法、减法、乘法、除法、乘方，教师选择一些进行板书）

问题3：举几个简单乘方运算的例子.（学生举出22=4，33=27，（-3）2=9等，可收集一部分板书在黑板上）

问题4：我们知道，加和减、乘和除都是互逆运算，它们的结果分别称和、差、积、商.乘方的结果称幂.现在逆过来研究乘方与幂，若已知幂、指数，求底数怎么算？（预设：学生求x2=4时，可能会漏掉-2.启发大家再次分析x2=9时，要考虑两解）

问题5：上面已知幂和指数，求底数的运算，就是乘方运算的逆运算，也就是第六种运算：开方运算.这么简单，为什么有理数那章没有顺便学习？

教学环节（二）研究数的开方

问题6：研究开方运算.

从最简单的开平方运算开始.

给出定义：上面已知道了4开平方得到2、-2；9开平方得到3、-3.我们把开平方得到的结果称为平方根.

跟进训练：9的平方根如何表示？3的平方根如何表示？5的平方根如何表示？

小结归纳：一个正数的平方根有两个，它们互为相反数；0的平方根为0；负数没有平方根.特别的，对于正数a的平方根中那个正的平方根，我们称之为a的算术平方根.

过渡：开平方也称开二次方，现在让我们拾级而上，研究开三次方，即开立方.

自主研究：将8开立方的结果是？你觉得开立方的结果取个什么名字？你能想到用怎样的符号表示它们吗？（对于数x来说，它的立方根记为）举几个例子来巩固理解一个数的立方根.

小结归纳：一个数的立方根有且只有一个.正数的立方根是正数，0的立方根是0，负数的立方根是负数.

教学环节（三）“数系”再次扩充

回顾：进入初中，引入负数之后，小学阶段的数系相应地扩充为有理数，我们也知道了整数与分数统称为有理数，也称可比数（m、n为整数，n≠0）.

数学史话链接：据传毕达哥拉斯学派的一个“门徒”希帕索斯率先发现了不是有理数，

图1

如图1，将两个边长为1的正方形分别沿它的对角线剪开，得到四个等腰直角三角形，即可拼成一个大正方形.容易知道，这个大正方形的面积是2，那么大正方形的边长为多少呢？

建立模型：待求的大正方形的面积为2，设它的边长为a，则有a2=2.也就是要把平方运算逆过来思考，即在幂的运算式子“an”中已知指数和幂，逆过来求底数的值.问题简化如下：

若a2=2，求a=_____（.答案为，负的平方根舍去）

因为这个“邪恶”的发现，不符合学派教义“万物皆备于数”，他被扔进了大海，也引发了“第一次数学危机”.随着数系扩充，从有理数系再次扩充到实数（有理数和无理数统称为实数），第一次数学危机就得到了解释.

研究展望：数系扩充之后，就需要进一步研究新数系的相关概念，如数轴、相反数、绝对值、大小比较，以及实数的运算，这些都将是后续学习的内容.

教学环节（四）回到“开平方”

应用1：解简单的一元二次方程.

解方程：（1）x2=16；（2）x2-25=0；（3）4x2=9.

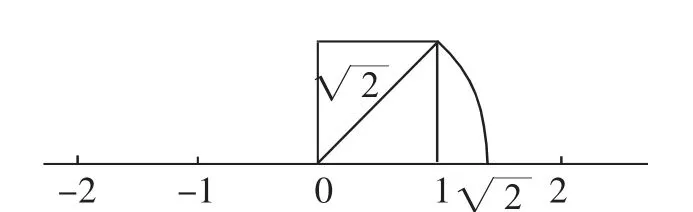
图2

图3

你能理解这种画法吗？能找到表示- 2 的点吗？

同类推介：如图3，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达O′点，那么O′点对应的数为π.

最后进行适当的小结，完善本节课结构化板书：

图4

二、教学立意的进一步阐释

1.教无定法，重视基于数学知识内在联系的角度引入新课

数学是科学，教学是艺术.教无定法，适合的就是好的.教材上引入平方根、数的开方自有其道理和依据，但是我们在上文中基于数学知识的内在联系，构思了从乘方的逆运算思考，定义并引出实数系及与之相关的数学新知，如平方根、无理数，特别是数系扩充到实数系之后，对于实数的相关概念、数轴、相反数等也带领学生进行了眺望和初步感知.从这个角度看，这种新知引入方式是符合教学实际的情境创设.

2.对话互动，通过系列问题串起教学进程并促进课堂生成

在上面课例中，通过一系列的问题串起了教学环节，同时启发学生思考，把学生的思维“卷入”到本课内容中来，学生积极思考，踊跃展示，得到了很多生成性资源，教师及时捕捉这些生成性资源并用于推进后续教学进程，生成、完善板书设计.让学生“不知不觉”感受到这节课的新知都是在他们参与下获得并丰富起来的，除了学得新知，探究数学的求知欲和自信心都能得到有效提升.

3.渗透文化，精心预设融入“数学史”激发学生参与的热情

数学是一种文化，几千年来与人类文明相伴始终.数学发展史也表明，像无理数这样的数学史话，特别是引发了“第一次数学危机”这样的重要内容，初中生在首次接触时，如果进行必要的“融入式”学习，则对于数学素养较好的学生来说，应该是一种精神的洗礼.所以，我们把毕达哥拉斯学派，特别是其门徒希帕索斯发现无理数的故事融入了新课教学进程，并运用后来欧氏几何原本中的证法向学生进行演示推介，对优秀学生来说，虽然这些都不是为了“眼前利益”而服务，但是为他们打开的这扇窗，对渗透数学文化、熏陶数学精神是十分有益的.