核心素养咋落地武汉试题有见地*
☉湖南省常德芷兰实验学校初中部陈金红
*基金项目:本文系全国教育科学“十二五”规划2013年度教育部规划课题“生命课堂视野下的教学案例研究”(课题编号:FHB130512)的成果之一.
各地中考题,基础全覆盖、形式各异,核心素养咋落地?武汉试题有见地:第10题翻折还原出惊奇;第16题条件离散难落地、特征构造露诡计;第23题三个小题,透出真谛,同型化归,相互帮衬就非难题!下面就谈谈这三题:
例题1:(2018年湖北武汉市中考数学卷第16题)如图1,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是______.

图1
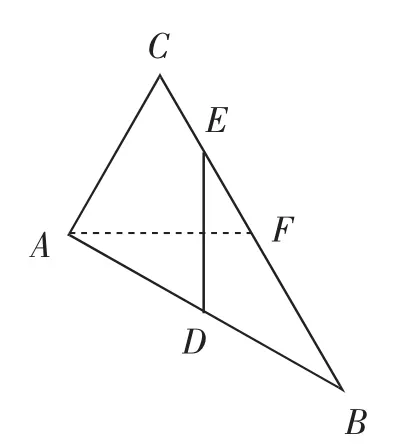
图2
1.思路解析
(1)针对已知条件“若DE平分△ABC的周长”,学生一般推理到BE=1+CE,或BC=1+2CE就止步了,如何再走方向不明!
要想前进必须联想,针对已知条件“∠ACB=60°,AC=1”,其实它是等边三角形的部分特征,“补美补全”构造出等边三角形即正△ACF,见图2.
(2)于是一个中间“链条”即正△ACF来“续”上,此时“临近”推理出AC=AF=CF=1,又可以计算推理出BF=BC-CF=(1+2CE)-1=2CE.学生一般推理到BF=2CE就止步了,如何再走方向又不明了!
要想前进必须联想,上面的中间结果“BF=2CE”是三角形中位线定理的结论之一,显然与△ABF相关联,此时“D是边AB的中点”乃已知条件!于是不妨取AF的中点G,连接DG,即得△ABF的中位线,且DG=BF=CE,见图3.
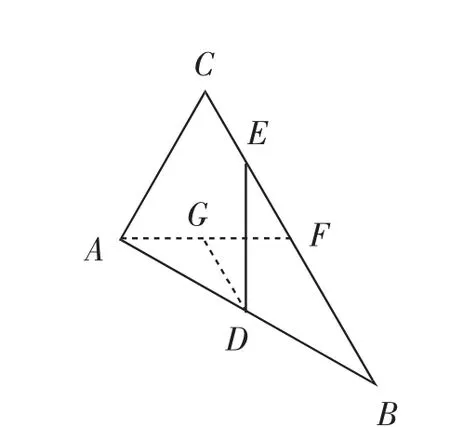
图3
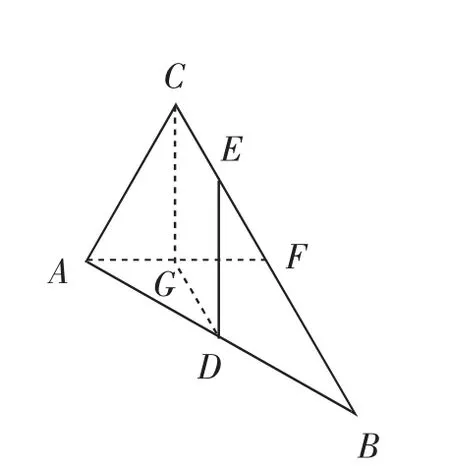
图4
(3)一般学生由于不习惯于借助“已知和中间推理出来的结论”和观察由此带来的“变化后的图形”,到图3也就止步了!
要想前进必须联想,上面的中间结果DG=CE,DG∥CE,即有“一组对边平行且相等”,此乃判定平行四边形的方法之一,连接CG,见图4,于是有平行四边形CGDE,于是所求DE即CG的长度!而CG所在的三角形是一个正三角形,边长为1,立即可以求得
显然是“推理、联想”同时上,交错着“攻击”前进的结果!
2.解答概要
(1)在边CB上取线段CF=AC,连接AF.因∠ACB=60°,可得正△ACF.
(2)又DE平分△ABC的周长,D是边AB的中点⇒BE=1+CE,或BC=1+2CE⇒BF=BC-CF=2CE.
(3)再取AF边的中点G,连接GD、CG.于是GD是△ABF的中位线,且DG=BF=CE,即DG=CE.又DG∥CE,则可得平行四边形CGDE⇒DE=CG.
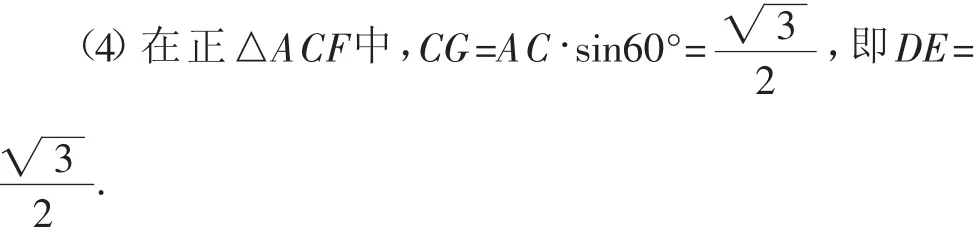
3.教学观察
(1)思路线索上:先直观分析出BE与CE的数量关系,通过计算推理演算再发现BC与AC、CE的数量关系(BC=1+2CE),由已知边AC长为1、∠ACB=60°,中间结论2CE,联想到构造正三角形、构造三角形中位线、构造平行四边形、构造直角三角形等,由此即彼地推理着、联想着、交错着,前进……逻辑思维环环相扣,推理和联想“步步惊心”.
(2)图形主要涉及:等边三角形、直角三角形、平行四边形.
(3)结论主要涉及:勾股定理或锐角三角函数的定义、三角形中位线定理、平行四边形的判定与性质.
(4)方法注要涉及:除了分析和综合法,就是构造法!
由上述不难体会出:虽是一道小小的填空题,却涉及图形、知识和方法不少且均是初中数学的重中之重,显然不失为一道考查学生学科核心素养的好题!考场上,数学压轴题(填空或大题)常常似曾相似,却又触手不可及,一般是因为问题条件过于“离散”,联系空间过于“旷阔”,已知和所求一时难以“牵手”,这也是我们研究中考答题的“节点”,一种有效的方式是:推理、联想同时“上”,交错“攻击”向前进,也就是:前进一步、再前进一步!
例题2:(2018年湖北武汉市中考数学卷第10题)如图5,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D.若⊙O的半径为,AB=4,则BC的长是().
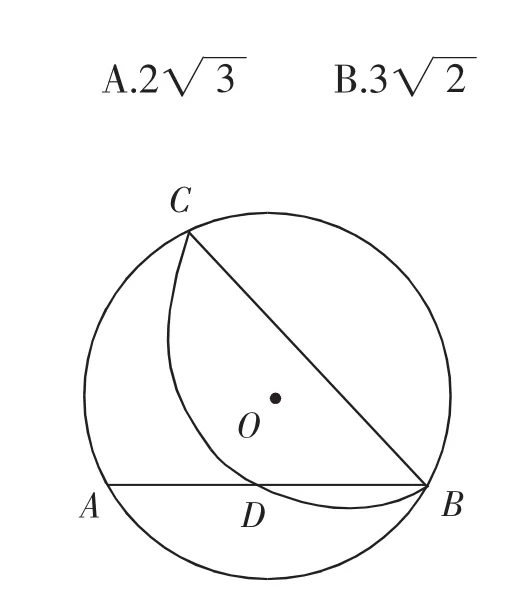
图5

图6
1.思路解析
要想前进必须联想,结合上面的中间结果AD=DB=AE=2,于是连接DE得EF,再连接BF得四边形FBCE.此时有两个特殊三角形,即等腰Rt△AED和等腰Rt△BFD,各边长即可求得,见图7.
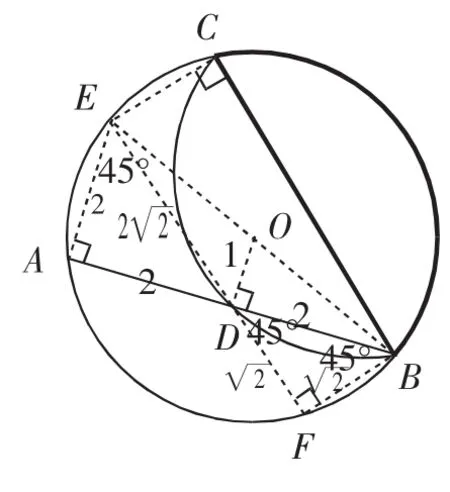
图7
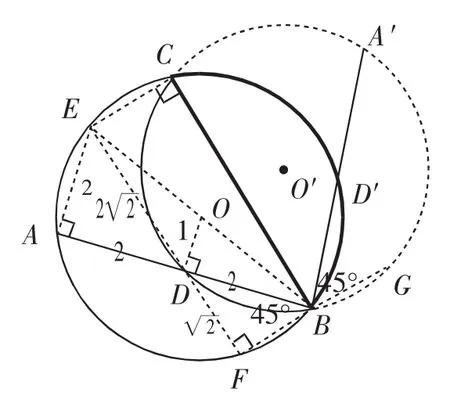
图8
(2)针对已知条件“将弧BC沿BC折叠后刚好经过AB的中点D”,好像“好处”就像上面所说的只能运用垂径定理,真的吗?
要想前进必须联想,要证明四边形FBCE是矩形,只差一个直角条件了,比如,证明出CB⊥BF即可达到目的!
用轴对称变换的观点看:弧BC(原像)的像是弧BDC,对称轴是BC所在的直线;⊙O的其他部分比如弧、弦及弦上的点比如点D等的原像呢?“一一还原”,见图8.
其实两个圆是等圆,所求BC是相交两等圆的公共弦,公共弦BC所在的直线是这两个等圆构成的整体图形的对称轴!立即可以推出:∠ABC=∠A′BC、∠ABF=∠A′BG=45°⇒BC⊥FB,结合∠C=∠F=90°,得四边形FBCE是矩形
2.解答概要
(1)连接OD,构造直径EB,连接AE、EC⇒OD=1、AD=DB=AE=2.
(2)连接DE得EF⇒等腰Rt△AED和等腰Rt△BFD及各边长.
(3)用轴对称变换的观点“一一还原”⊙O的各个部分比如弧、弦及弦上的点比如点D等的原像⇒∠ABC=∠A′BC、∠ABF=∠A′BG=45°⇒BC⊥FB,结合∠C=∠F=90°,可得四边形FBCE是矩形
3.教学观察
先是条件自然发散即可得出“一串串”中间过渡但很有价值的信息,很有人情味的“诱导”设计;至此解题思路“戛然而止”,凸显“翻折”条件如果只是“蜻蜓点水”式的“挖掘”是不可能轻易解决问题的,如果对几何变换做整体完整的直观理解,必是:像寻原像,图形补全,推出轴对称图形,从而突破“翻折”条件“黑障区”,思路豁然开朗!可见学科核心素养的落地,问题载体恰当与否决定成败,其中问题即有直观可以感受的信息源,亦必须有“只有充分”挖掘才可前进的“资本”,启迪我们的教学方向:理念问题化,问题要有“设计”,这个“设计”就是要有思维“黑障区”!
例题3:(2018年湖北武汉市中考数学卷第23题)在△ABC中,∠ABC=90°.
(1)如图9,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM △BCN.
(2)如图10,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值.
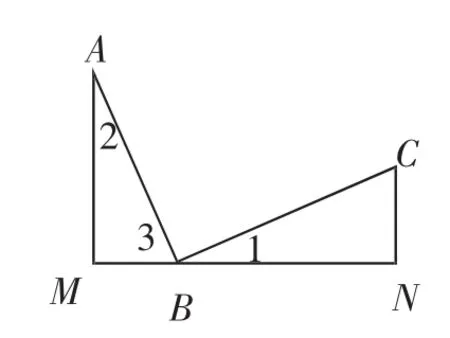
图9
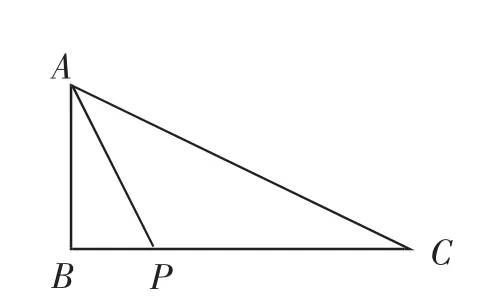
图10
(3)如图11,D是边CA的延长线上一点,AE=AB,∠DEB=,直接写出tan∠CEB的值.
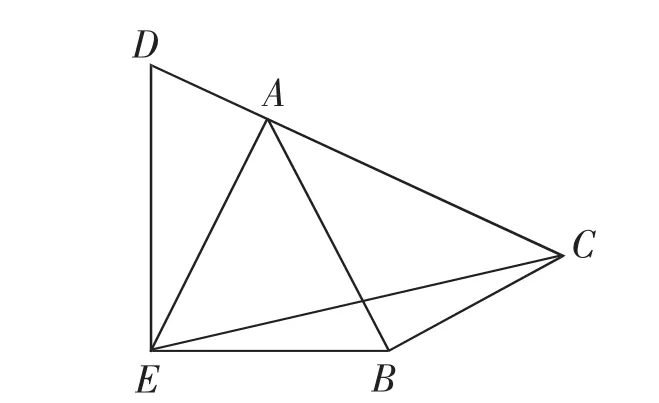
图11
1.思路解析
对于(1),在两个已知的直角三角形ABM与直角三角形CBN中,有很多角角关系如互余,再加上∠ABC=90°,与顶点B处的两个锐角结合,又会产生新的角角关系如互余或相等,立即可得所证的三角形相似.若连接AC,立即可得菲尔德总统证明勾股定理的“模型图”.
对于(2),结合第(1)小题的“模型图”,构造如下:
过P点作PN⊥AP交AC于N点,过N作NM⊥BC于M点;Rt△MNC左边的图形四边形ABMN就是“模型图”.
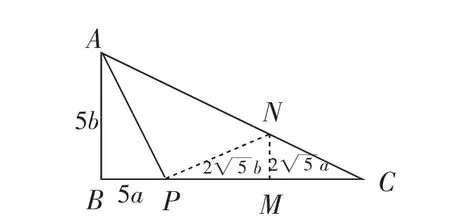
图12
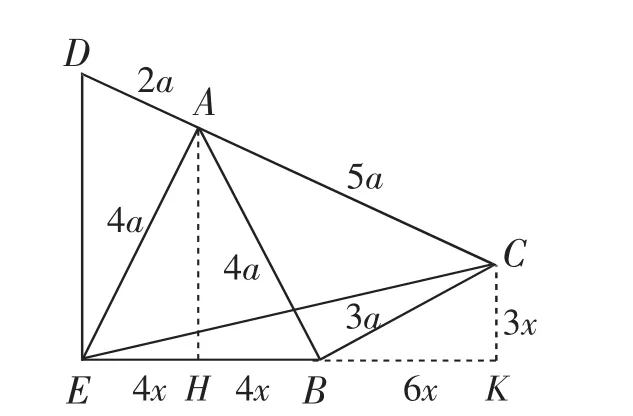
图13
对于(3),同样结合第(1)小题的“模型图”,构造如下:
过A作AH⊥EB交EB于H,过C作CK⊥EB交EB的延长线于K;四边形AHKC就是“模型图”.
2.解答概要
(1)一对直角及同角的余角相等⇒∠1=∠2⇒△ABM△BCN.
(2)过P点作PN⊥AP交AC于N点,过N作NM⊥BC于M点.易得△BAP △MPN

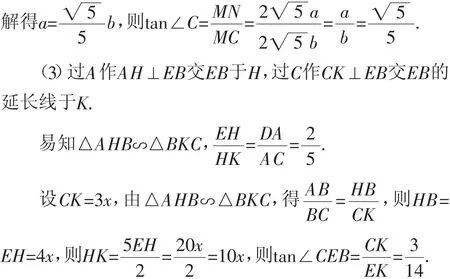
3.教学观察
小题之间,貌似独立,实则联系:题(1)乃基本相似,其实就是直角三角形勾股定理的“菲尔德总统证明方法”模型图;题(2)可化归于(1),图不同路同,同型化归路通透,信息充足立可求;题(3)仍化归为(1)之模型图,思路清晰、利索干净!总是仿(1)构图就是模型图,题(1)铺路,承前启后,方法照旧,模型点睛,问题定清!启迪我们的教学方向:难题教学分解的“脚手架”和“模型图”是“桥梁”,关键在于要有“设计”!使学生内化理念:站在题目的“肩膀上”,会使我们入题快、想得深、速得分,学科素养“亮晶晶”!
毋须多例,由上面三题的教学赏析不难得出:无论是从考查内容、问题的设计,还是知识覆盖、思维程度、纵横跨度无不让人点赞,还有更多好题,限于篇幅,建议收集查悉,因此我妄言:数学素养落地于问题,问题承载价值要设计,设计“看齐”武汉题,教学指导接地气!

