化归思想在初中数学课堂中的应用

☉江苏省南通市通州区平潮实验初中刘惠云

化归是数学的重要思想，其本质就是一种转化思维，将陌生场景转化为人们熟悉的场景，进而实现由难到易、删繁就简的效果.在初中数学中，化归思想最常见的用法主要体现在多元方程转化为一元方程、高次方程转化为低次方程、代数问题和几何问题的相互转化、实际问题向数学问题转化等.由此可见，化归思想在初中阶段有着非常广泛的应用.为此，教师在初中数学课堂上要注重化归思想的教学，并且让学生能够运用化归思想处理问题.

一、结合学科特点及学情特点实施化归思想教学

新修订的课程标准将学生数学核心素养的发展纳入了培养体系，虽然核心素养并没有对应某项具体的技能和方法，但是其中数学抽象、逻辑推理、数学建模、直观想象等方面的能力都和化归思想有关联，因此在初中数学教学中，有针对性地实施化归思想的教学是课程标准的基本要求.

很多教师在教学中有这样的认识：化归思想是一种隐性知识，这些内容不能通过教师的口头说教来组织，应该让学生在自主探索中实现感悟和积累经验，这其实不需要教师专门的指导，只要多给学生安排一些习题，多做做就有感觉了.笔者认为上面的观点只对了前一半.的确，作为一种隐性知识，如果仅靠教师的口头说教，是没有任何意义的，不但浪费时间，甚至可能导致学生产生一种逆反的心理和情绪.但是教师不能缺席学生在数学思想方面的成长，毕竟数学本身就具有高度的抽象性，而数学思想的抽象程度还要更高，根本无法通过图表进行总结，如果让学生自己摸索，显然是没有意义的.

相比于小学生，初中生在抽象思维方面已经有一定程度的发展，这时引导学生探索包括化归思想在内的数学思想正是一个很好的时机.而且很多问题的分析恰好要借助化归思想，为此我们以相关问题为素材，正好可以引导学生边探索边总结，指导学生有效掌握这一方法的使用条件和操作要点.比如，在学生学习七年级的数学内容时，他们将接触负数和代数式等内容，他们对这些都是相当陌生的，对很多学生来讲，这些内容的理解和使用是很不习惯的.为此，教师要引导学生采用化归思想，将这些陌生的内容和他们已有的认知体系联系起来，可以通过一根数轴，将负数和正数放在一起，还可以通过绝对值的处理将负数转化为整数.

当然，化归思想不是一两节课就能解决的，它贯穿在学生整个初中数学的学习过程中，教师应该有一个长远的计划，将化归思想纳入整个初中数学的教学框架，让学生在建构数学知识体系的同时领悟隐含在其中的方法和规律，进而形成自主运用化归思想的意识.

二、通过典型案例揭示化归思想的操作过程

初中数学教师普遍存在这样的困惑，习题讲过不少，但是学生的能力始终停留在模仿的层面，相关条件略有变动，他们就手足无措，更谈不上在问题分析过程中区分在哪些情况下选择化归思想.笔者认为，学生出现这样的问题，往往是因为教师在教学过程中就题论题，很少通过深度挖掘来帮助学生进行思想方法的总结.因此，笔者认为，应该在教学中放慢节奏，引导学生感悟思路的探索过程，进而让他们了解化归思想的方方面面，同时这能启发学生以典型问题为范本总结化归思想的操作特点，进而在遇到类似问题时，学生能够做到从容不迫，成竹在胸.

在指导学生探索某些定理时，教师要注意到某些证明过程本身就是一个最典型的探究素材，教师在教学设计时，要注意发掘隐含在其中的数学思想和方法，如化归思想.教师引导学生围绕对应的问题情境展开分析，不但可以加深学生对原理的理解，而且能提升他们的知识迁移水平.

比如，对于圆周角定理的证明，我们就可以结合化归思想的教学进行设计，化归的常见策略应该是推动一般问题的特殊化.所以在探索这一原理时，教师可以引导学生先探索圆心位于圆周角一条边上的场景，然后提供圆心位于圆周角外部或内部的场景，并将其转化为之前的特殊场景，实现问题的简化处理.

问题情境：图1所示的⊙O中，圆弧BC所对应的圆心角为∠BOC，圆周角为∠BAC，请研究这两个角在大小上的关系.

情境拓展1：如果圆心与圆周角的位置关系如图2所示，圆心位于圆周角的内部，请研究这两个角在大小上的关系.

情境拓展2：如果圆心与圆周角的位置关系如图3所示，圆心位于圆周角的外部，请研究这两个角在大小上的关系.

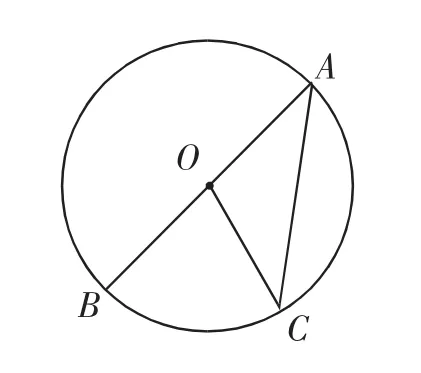
图1

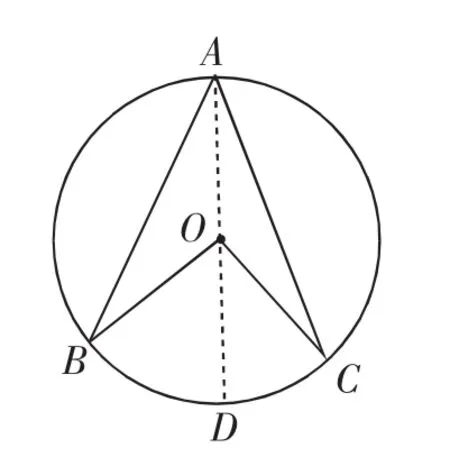
图2

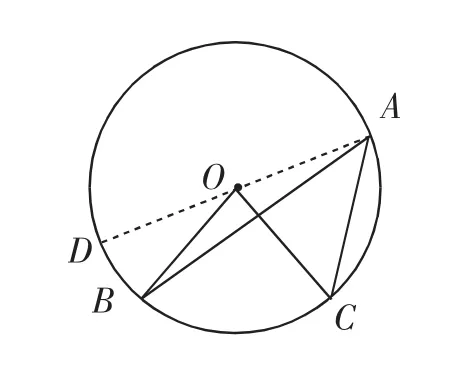
图3

在最初的问题情境中，学生可以很快利用三角形的外角与内角的关系实现问题的分析和处理，但是情境拓展之后的情形则相对一般，怎么处理呢？教师要引导学生比较问题之间的差别，同时要有意识地引导学生通过建构图2和图3中的辅助线将其转化为图1所示的特殊场景，如此则能实现问题的解决.当学生完成这个问题后，教师还要有意识地引导他们展开总结，提炼出化归思想的操作过程.

三、让学生通过有效的习题训练获得提升

化归思想的培养不能依赖于习题的讲练来实现，但是没有习题训练，显然是不行的.在实际教学过程中，教师要关注习题的有效设计.这些习题宜精不宜多，须知太多的题量只会让学生产生一种应付的心态，而且题量太多，学生的时间又是有限的，他们显然不会再花时间进行反思和总结.所以，教师要注意选择具有代表性的习题，在条件允许的前提下，教师要适当通过变式教学对问题进行补充和延展，这样可以让学生的化归思想得到更加深入的发展，他们的思维水平也将因此而获得提升.

（1）请确定A、B两点的坐标；

（2）求解△AOB的面积.

在处理问题（1）时，可以将函数问题化归为方程组问题.由方程组A、B两点的坐标可以确定为A（-2，4）和B（4，-2）.

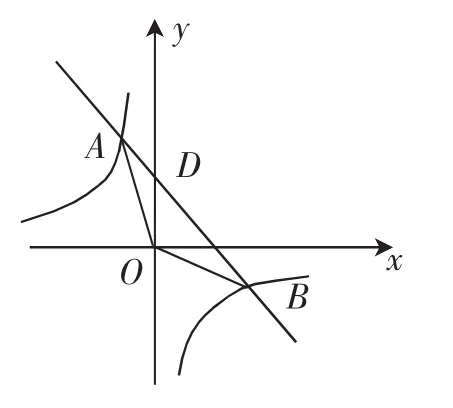
图4

至于第（2）问，由图像可知直线y=-x+2与y轴的交点D的坐标是（0，2），因此所以S△AOB=2+4=6.

上述问题中的交点坐标既满足第一个函数，又匹配第二个函数，因此可以将其转化为方程组，这个题目也提示学生关注方程与函数之间的关联，由此为他们提供化归的思路.

习题练习绝不是数学研究的全部，但是能充分地将包括化归思想在内的各种方法和技巧有效体现出来.教学过程中，教师通过习题来引导学生探索并积累化归处理的经验，有些时候，某个问题的化归处理思路不止一个，这时教师可以提示学生采用多样化的化归方法处理，通过一题多解来提升学生思维的灵活性.当然，有时候学生采用一种方法进行化归处理时，很可能陷入僵局，这时教师要注意提醒学生及时调整思路，或安排学生在合作探究中进行更加深入的讨论，以便实现问题的解决.

综上所述，作为初中数学研究的一种重要思想，化归思想的培养需要教师足够的注意，也需要教师在教学中有策略地予以推进.