数学教学，应注重反思

☉山东省莱芜市雪野旅游区雪野镇中心中学王德军

反思是数学学习中一个非常重要的环节，同时是一个良好的数学习惯和思维品质.美国著名数学教育家乔治·波利亚曾经说过：“数学问题的解决仅仅成功了一半，更重要的是解题后的反思.”由此可见反思的重要性.

不断对所学的数学知识和解决的问题进行反思，能够深化对问题的理解，拓展解题思维途径，揭示问题的本质和规律，促进知识的同化、迁移和应用，沟通知识之间的纵横联系.下面举例说明如何在数学学习中进行反思.

一、反思问题的其他解法

俗话说：“条条大路通罗马.”很多数学问题的解法往往并不止一种.另外，由于不同学生对同一问题的思考方法不一样，因而解法往往会因人而异，但都可以得到问题的正确结果.因此我们在解决数学问题时，不能仅满足于将问题解答出来，解答完毕之后还应该思考这个问题还有没有其他的解决方法，并尝试运用另外的方法进行解答.例如，下面这样一道证明题：如图1，在△ABC中，AB=AC，点P是BC边上任意一点，PD和PE分别是AB、AC边上的高.求证：CF=PD+PE.

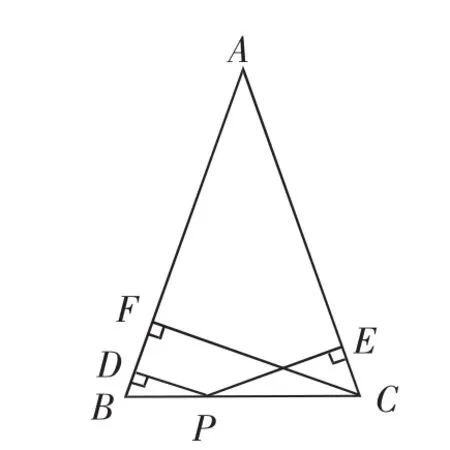
图1

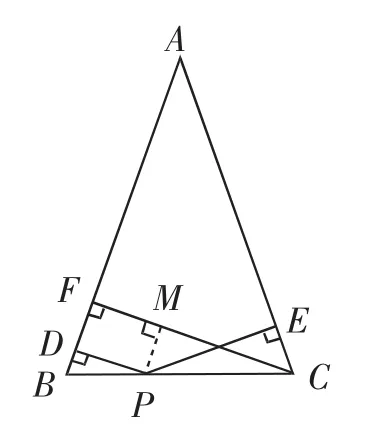
图2

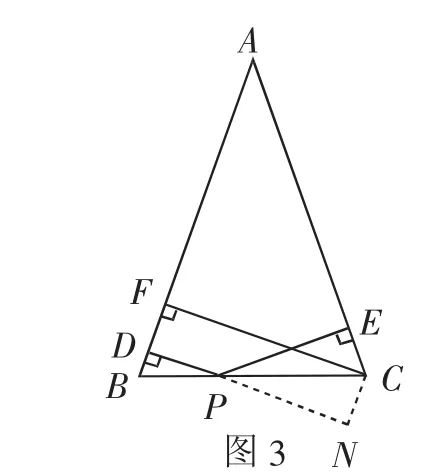
图3

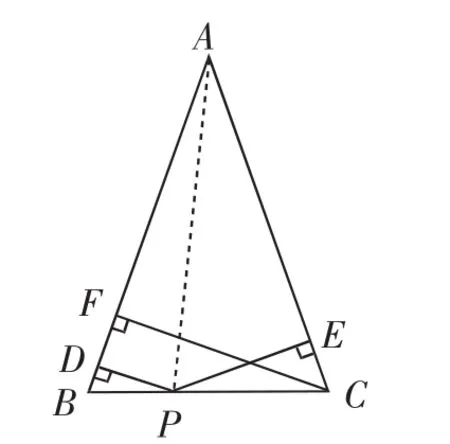
图4

证明该题，既可运用截长法，即过点P作PM⊥CF于M（如图2），容易证明四边形PMFD是矩形，从而PD=FM.然后证剩下的线段CM与PE相等.可通过证明△PCM与△CPE全等实现.也可运用截短法，即过点C作CN⊥DP交DP的延长线于点N（如图3），容易证明四边形NCFD是矩形，从而CF=DN.然后证延长的线段PN与PE相等.可通过证明△CPN与△CPE全等实现.无论是截长法还是补短法，都需要证明三角形全等，比较麻烦.注意到题目条件中的高，联想到三角形的面积公式，因此可以借助三角形面积之间的关系巧证本题.即连接AP（如图4），利用△ABC的面积等于△ABP与△ACP的面积之和证明.另外，在学习了三角函数的知识之后，本题还可应用三角函数进行巧证. 易知PD=BP·sin∠ABC，PE=CP·sin∠ACB，CF=BC·sin∠ABC，然后利用BC=BP+CP可以简捷证明本题.

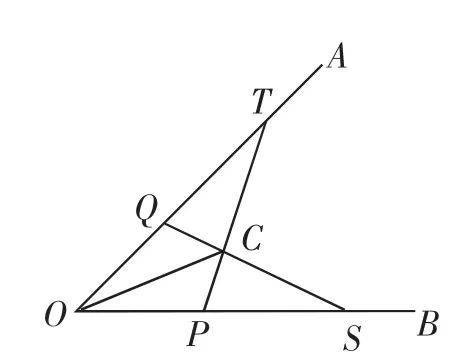
图5

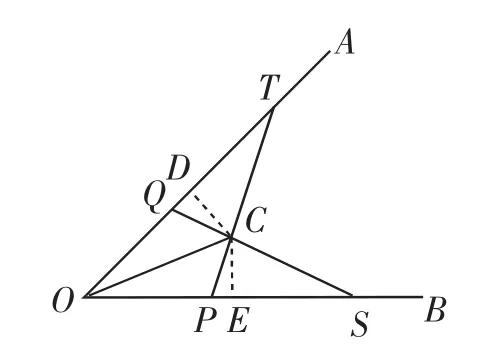
图6

再如下面一道证明题：如图5，在∠AOB的两边OA、OB上分别取OQ=OP，OT=OS，PT和QS相交于点C.求证：OC平分∠AOB.本题的常规证法是先证△OPT△OQS，得到∠OTP=∠OSQ.再证△QCT△PCS，得到QC=PC.再证△QCO△PCO，得到∠AOC=∠BOC，从而OC平分∠AOB.需要三次证明三角形全等，虽然思路简单，但过程比较麻烦.结合待证结论，自然联想到角的平分线性质定理的逆定理“到一个角的两边相等的点在这个角的平分线上”，可过点C分别作∠AOB两边的垂线.并结合面积进行证明.如图6，分别过点C作CD⊥OA，CE⊥OB，垂足分别为D、E.可先证△OPT△OQS，得到S△OPT=S△OQS.进而易证S△QCT=S△PCS.根据已知条件很容易证明QT=PS，从而CD=CE.则OC平分∠AOB.这种证明方法只需证明一次三角形全等，相对来说比较简捷.

二、反思问题之间的联系

我们所学的数学知识前后是相互联系的，而不是孤立的，我们要用联系的观点学习数学知识，将所学的数学知识有机整合在一起，构建知识“集成块”.要用联系的观点看待数学问题，抓住数学问题之间的联系，从而把握问题的本质.

先看这样两个数学问题：

题1：如图6，在正方形ABCD中，E是BC边上任意一点，CF是外角平分线，若∠AEF=90°，求证：AE=EF.

题2：如图7，在正三角形ABC中，M是BC边上任意一点，P是BC的延长线上一点，N是∠ACP的平分线上一点，若∠AMN=60°，则AM=MN是否成立？

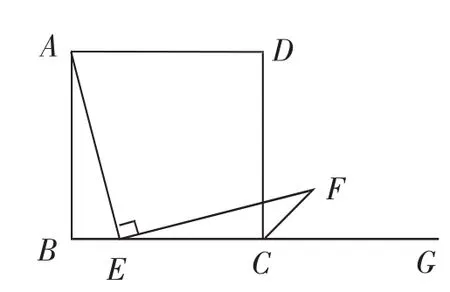
图7

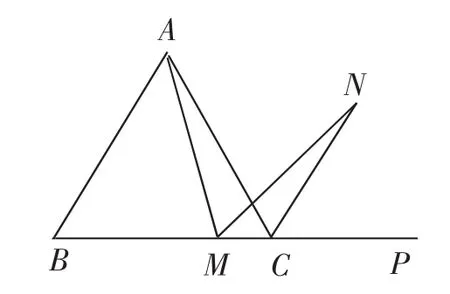
图8

表面上看，这两个问题有点儿风马牛不相及，毫不相干，一个以四边形为载体，一个以三角形为载体，实际上，这两个问题从题目条件到结论还有证明方法都非常相似.首先，正方形和正三角形都是正多边形，CF和CN都是外角平分线，∠AEF=90°与∠AMN=60°都等于正多边形的一个内角，待证结论都是证明两条类似的线段相等.图6中的A、E、C、F四点共圆，图7中的A、M、C、N四点共圆.再看证明方法，两个题目都可以运用截长法和补短法构造全等非直角三角形证明；也可通过构造全等直角三角形证明；还可通过构造等腰三角形证明（要用到四点共圆）.通过比较不难发现，问题1和问题2实际上是同一问题的“不同表现形式”，本质是一样的.

再看下面三个问题：

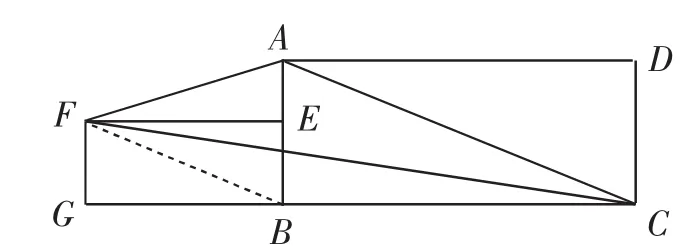
图9

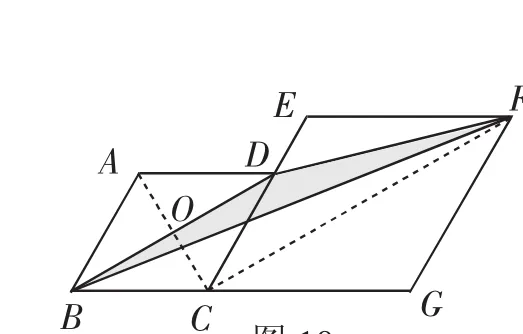
图10

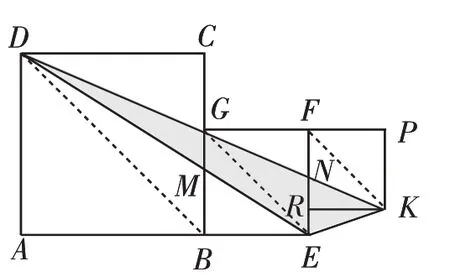
图11

图11

题1：如图8，矩形ABCD中，AB=3cm，AD=6cm，点E为AB边上任意一点，四边形EFGB也是矩形，且EF=2BE，则S△AFC=________cm2.

题2：如图9，菱形ABCD和菱形ECGF的边长分别为2和3，∠DAB=120°，则图中阴影部分的面积是（）.

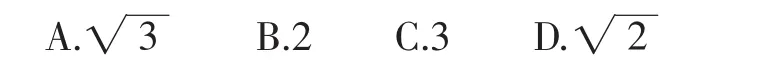
题3：正方形ABCD、正方形BEFG和正方形RKPF的位置如图10所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为________.

上面三个问题表面上看也不相干，实际上是同一问题的“不同表现形式”.题1中的矩形EFGB和矩形ABCD相似，题2中的菱形ABCD和菱形ECGF也相似，题3是把菱形改成了正方形，而且多加了一个正方形.三个问题都可以利用代数方法直接计算，也可以利用几何方法，通过构造平行线，利用等底等高的三角形面积相等求解.

通过比较不同数学问题的已知条件、数字特征、图形特征、待证结论，同时对其反思，我们抓住了表面上看起来不同的数学问题之间的联系，把握了问题的本质.

三、反思问题的解法是否合理

数学中的选择题和填空题是一类只注意结果而不注重过程的试题，而解答题和证明题是一类需要写出解答（证明）过程的试题.我们曾经遇到过这样的现象：有些学生的解答（证明）过程出现错误但结果是正确的，有时中间出现的错误非常隐蔽，不易发现.因此，我们有必要对问题的解答（证明）过程进行反思.先看下面一道看似简单的几何证明题：

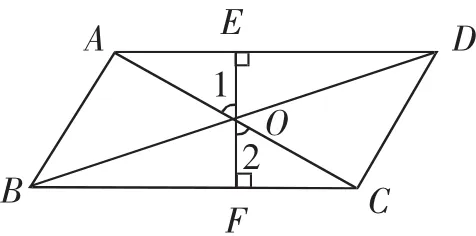
图12

已知：如图11，▱ABCD中，对角线AC、BD相交于点O，过点O分别作OE⊥AD于E，OF⊥BC于F. 求证：OE=OF.

一些学生是这样证明的：

由▱ABCD的对角线AC、BD相交于点O，得OA=OC.

由OE⊥AD，OF⊥BC，得∠AEO=∠CFO=90°.

又∠1=∠2（对顶角相等），则△AOE△COF.

则OE=OF.

上述证明表面上看似乎天衣无缝，但为什么有∠1=∠2？证明者实质上是默认了E、O、F三点共线，但原题设中没有说明E、O、F三点共线，故不能肯定∠1和∠2是对顶角，因此需要补证E、O、F三点共线.

可以说，上面的错误比较隐蔽，如果不对证明过程进行反思，很难发现这个错误.当然，由于证明∠1=∠2比较麻烦，但证明∠EAO=∠FCO比较简单，因此可从证明∠EAO=∠FCO入手证明△AOE△COF.另外，注意到条件“OE⊥AD，OF⊥BC”，联想到全等三角形对应边上的高相等，也可以考虑证明△AOD△COB.

以上仅从三个方面谈了在数学学习过程中如何进行反思.当然，数学中的反思包括很多方面：对数学中相似定理进行反思，如三角形全等的判定方法有“边边边”“边角边”“角边角”“角角边”“斜边、直角边”，而三角形相似的判定方法有“边边边”“边角边”“角角”“斜边、直角边”，对三角形全等和相似判定方法的异同点进行反思；对数学定理、性质中的规定进行反思，如等式性质2“等式两边乘同一个数，或除以同一个不为0的数，结果仍相等”，为什么要加上“不为0”这个限制条件？而等式性质1“等式两边加（或减）同一个数（或式子），结果仍相等”为什么没有加“不为0”这个限制条件？反思对于同一个数学题目哪种解法简捷，哪种解法更容易想出……

在平时学习数学知识的过程中，我们要养成反思的好习惯，经常进行数学反思.这样不仅有助于抓住数学知识之间的联系，揭示数学问题的本质，提高我们解决数学问题的能力，同时有助于提高我们的数学素养，构建自己的知识框架.W