一则数学趣题中的思维

☉山东省莱芜市雪野旅游区雪野镇中心中学张秀玲

图1表示一个4×4的正方形网格，你能数出图1中一共有多少个正方形吗？

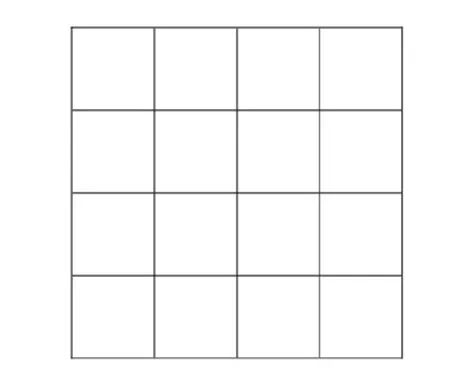
图1

这个问题看似不难，如果不假思索，贸然去数，极易出错.要么多数，要么漏数.那么，怎样才能既不重复也不遗漏地数出图1中所有正方形的个数呢？一个好的办法是分类.可以从正方形的边长入手对正方形进行分类，将正方形分成四类：（1）边长为1的正方形（16）；（2）边长为2的正方形（3+3+3=9）；（3）边长为3的正方形（2+2=4）；（4）边长为4的正方形（1）.所以图1中所有正方形的个数为16+9+4+1=30.

在解决上面趣题的过程中，我们从正方形的边长入手（当然也可从正方形的面积入手），对所有的正方形进行分类，最后将各种情况下得到的正方形个数相加，圆满求得正方形的总数.这里渗透了一种重要的数学思维方式：分类.这种将某种对象的全体，按照一定的标准，不重复、不遗漏地划分为若干部分或多种情况，称为分类.日常生活中分类的例子是很多的，比如，班上的学生如按性别划分，可以分为男生和女生两大类；按出生年月划分，又可以分为一月份生的、二月份生的、…、十二月份生的这十二类.对于一个较为复杂的问题，通过分类，将其分为若干较为简单的问题，然后对每个较为简单的问题各个击破，从而使整个问题最终获解.下面以例说明分类思想在解决数学问题中的应用.

一、当代数式中的字母具有不确定性时，需要对字母进行分类讨论

一般情况下，代数式中的字母既可表示正数，也可表示负数，还可表示0；既可表示有理数，也可表示无理数.很多含有字母的问题，大都需要对字母进行讨论.至于该按什么情况分类，应根据问题的需要而定.如在求|2a|=____时，就需要对字母a按照正数、负数和零进行分类讨论.再如化简+|a-3|时，需要分a≤-2、-2＜a＜3和a≥3三种情况进行分类讨论.

例1已知|a|=3，|b|=2，且a+b＞0，求a-b的值.

分析：由|a|=3，|b|=2，得a=±3，b=±2.由于字母a、b的值具有不确定性，因此需要分类讨论.

解：由|a|=3，|b|=2，得a=±3，b=±2.

当字母a、b同号时：

（1）当a=3，b=2时，a+b=3+2=5，符合题意，此时a-b=3-2=1；

（2）当a=-3，b=-2时，a+b=（-3）+（-2）=-5，不合题意.

当字母a、b异号时：

（1）当a=3，b=-2时，a+b=3+（-2）=1，符合题意，此时a-b=3-（-2）=5；

（2）当a=-3，b=2时，a+b=（-3）+2=-1，不合题意.

综上所述，a-b的值为5或1.

评注：在进行分类讨论时，应按照一定的标准将所有的情况全部罗列出来，并且注意根据题目的条件排除不符合题意的情况，如本例中应排除不符合“a+b＞0”这个条件下得出的a-b之值.

二、当几何图形的形状（线或点的位置等）具有不确定性时，需要进行分类讨论

在平面几何教学中，经常要对几何图形进行分类.例如，对三角形进行分类，既可按边分，也可按角分.

按边的相等关系分类如下：

再如推导圆周角定理时，根据圆心与圆周角的位置关系，可将图形分为三类：（1）圆心在圆周角内；（2）圆心在圆周角上；（3）圆心在圆周角外.当几何图形的形状（线或点的位置等）具有不确定性时，需要对几何图形的形状（线或点的位置等）进行分类，这样得出的结论才全面，得到的定理才无懈可击.同样在解决与几何图形有关的数学问题时，也要注意分类讨论，以免出现由于考虑问题不全面而得到片面甚至错误的结论.

例2已知坐标平面内一点A（2，-1），O为原点，P是x轴上一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（）.

A.2B.3C.4D.5

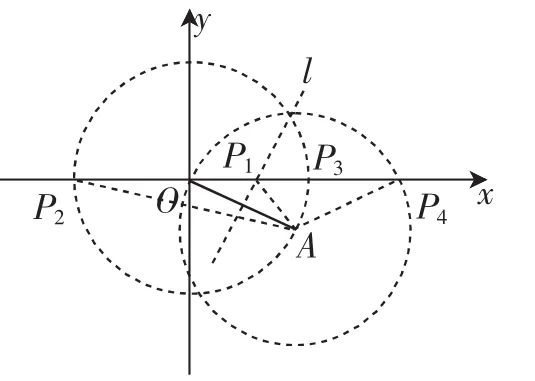
图2

解析：OA可能为底边，也可能是腰，因此需要分情况讨论.

（1）当OA为底边时，作OA的垂直平分线l交x轴于点P1，则△OP1A是以点P1为顶点的等腰三角形.

（2）当OA为腰时：以点O为圆心，以OA为半径画圆，交x轴于点P2、P3，则△P2OA和P3、OA是以点O为顶点的等腰三角形，以点A为圆心，以OA为半径画圆，交x轴于点O和点P4，则△P4OA是以点A为顶点的等腰三角形.

所以符合条件的动点P的个数为4，答案为C.

点评：涉及等腰三角形的问题经常需要分类讨论，讨论时既可按照底边和腰进行讨论，也可按照底角和顶角进行讨论，一切要视实际情况而定.另外，从本例不难发现已知一条线段求符合条件的等腰三角形的顶点的个数的方法：作已知线段的垂直平分线，或以已知线段的一个端点为圆心、已知线段长为半径画圆，垂直平分线或圆与相关直线的交点即为符合条件的等腰三角形的顶点.

三、当实际问题中的函数解析式具有不确定性时，需要进行分类讨论

在解决有关函数的实际问题时，自变量的取值范围有时要分成几段，在不同的范围内函数表达式往往不同.如在不同的时间段内，或者某一动点在不同的位置时等，得到的函数表达式就不同.这时我们在求函数表达式时，就要根据实际情况进行分类讨论.

例3襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下，把一片坡地改造后种植了优质水果蓝莓，今年正式上市销售.在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克.第x天的售价为y元/千克，y关于x的函数解析式为且第12天的售价为32元/千克，第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克，每天的利润是W（利润=销售收入-成本）.

（1）m=_______，n=_______；

（2）销售蓝莓第几天时，当天的利润最大？最大利润是多少？

（3）在销售蓝莓的30天中，当天利润不低于870元的共有多少天？

分析：问题（1）比较简单，可根据第12天的售价和第26天的售价快速求解.对于问题（2），首先要求出利润的函数表达式.在求利润的函数表达式时，由于售价的函数表达式分1≤x＜20和20≤x≤30两种情况，因此利润的函数表达式也应分两种情况.解答问题（3）时，仍然要根据两种不同的函数表达式借助二次函数的图像求解.

解：（1）由12m-76m=32，得m=-0.5.显然n=25.

（2）第x天的销售量为20+4（x-1）=4x+16.

当1≤x＜20时，W=（4x+16）（-0.5x+38-18）=-2x2+72x+320=-2（x-18）2+968.

则当x=18时，W最大值=968.

当20≤x≤30时，W=（4x+16）（25-18）=28x+112.

由28＞0，得W随x的增大而增大.

则当x=30时，W最大值=952.

968＞952，则W最大值=968.

令-2x2+72x+320=870，解得x1=25，x2=11.

由抛物线W=-2x2+72x+320的开口向下，得当11≤x＜25时，W≥870.则11≤x＜20.

又x为正整数，则9天利润不低于870元.

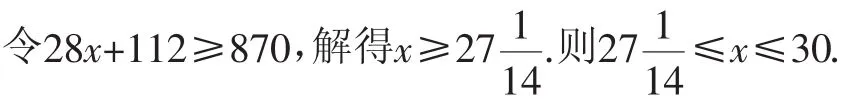
又x为正整数，则有3天利润不低于870元.

综上所述，当天利润不低于870元的共有12天.

点评：解答本题的重点是求利润W的函数表达式，难点是求当天利润不低于870元的天数.无论是求利润W的函数表达式，还是求当天利润不低于870元的天数，都需要分两种情况讨论.另外，需要说明的是，在求W的最大值时，需要将两种情况下求出的最大值进行比较，将其中较大的值作为W的最大值；在求当天利润不低于870元的天数时，需要将两种情况下求出的天数相加，结果才是当天利润不低于870元的天数.

以上我们仅从三个方面谈论了分类讨论思想在解答初中数学问题中的应用.事实上，分类讨论思想在初中数学教学中应用非常广泛，可以说分类讨论思想贯穿初中数学教学的全过程.在今后的数学教学中，我们要多加留意，多总结分类讨论思想的应用，这对于培养学生缜密的思维品质大有裨益.W